Hierarchical control and learning of a foraging CyberOctopus

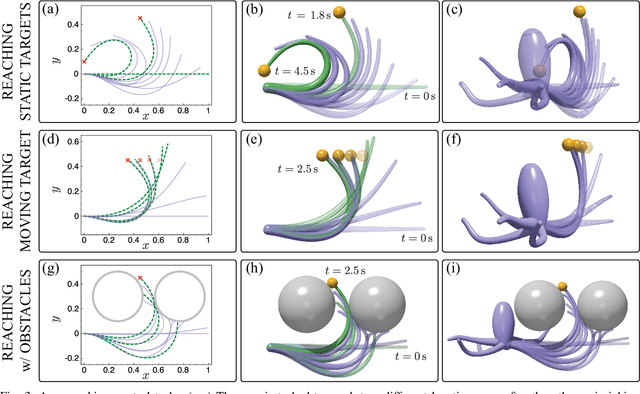
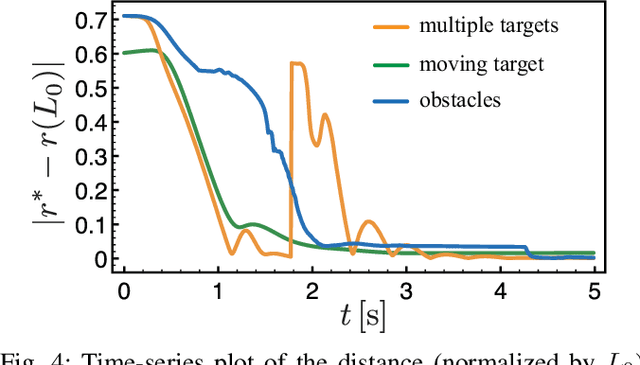
Inspired by the unique neurophysiology of the octopus, we propose a hierarchical framework that simplifies the coordination of multiple soft arms by decomposing control into high-level decision making, low-level motor activation, and local reflexive behaviors via sensory feedback. When evaluated in the illustrative problem of a model octopus foraging for food, this hierarchical decomposition results in significant improvements relative to end-to-end methods. Performance is achieved through a mixed-modes approach, whereby qualitatively different tasks are addressed via complementary control schemes. Here, model-free reinforcement learning is employed for high-level decision-making, while model-based energy shaping takes care of arm-level motor execution. To render the pairing computationally tenable, a novel neural-network energy shaping (NN-ES) controller is developed, achieving accurate motions with time-to-solutions 200 times faster than previous attempts. Our hierarchical framework is then successfully deployed in increasingly challenging foraging scenarios, including an arena littered with obstacles in 3D space, demonstrating the viability of our approach.

Energy Shaping Control of a Muscular Octopus Arm Moving in Three Dimensions

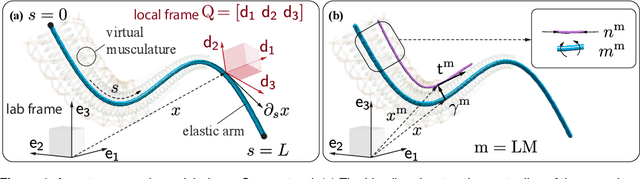
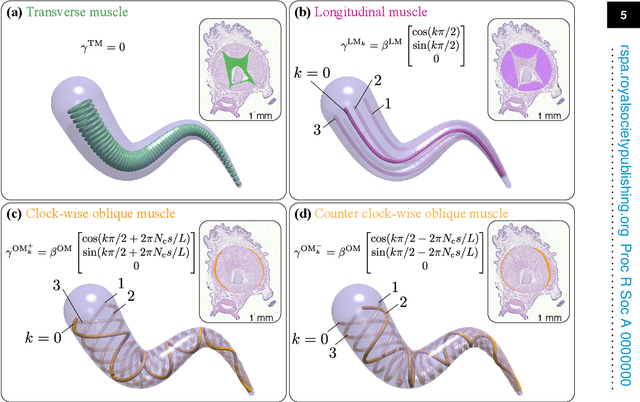
Flexible octopus arms exhibit an exceptional ability to coordinate large numbers of degrees of freedom and perform complex manipulation tasks. As a consequence, these systems continue to attract the attention of biologists and roboticists alike. In this paper, we develop a three-dimensional model of a soft octopus arm, equipped with biomechanically realistic muscle actuation. Internal forces and couples exerted by all major muscle groups are considered. An energy shaping control method is described to coordinate muscle activity so as to grasp and reach in 3D space. Key contributions of this paper are: (i) modeling of major muscle groups to elicit three-dimensional movements; (ii) a mathematical formulation for muscle activations based on a stored energy function; and (iii) a computationally efficient procedure to design task-specific equilibrium configurations, obtained by solving an optimization problem in the Special Euclidean group SE(3). Muscle controls are then iteratively computed based on the co-state variable arising from the solution of the optimization problem. The approach is numerically demonstrated in the physically accurate software environment Elastica. Results of numerical experiments mimicking observed octopus behaviors are reported.

A physics-informed, vision-based method to reconstruct all deformation modes in slender bodies

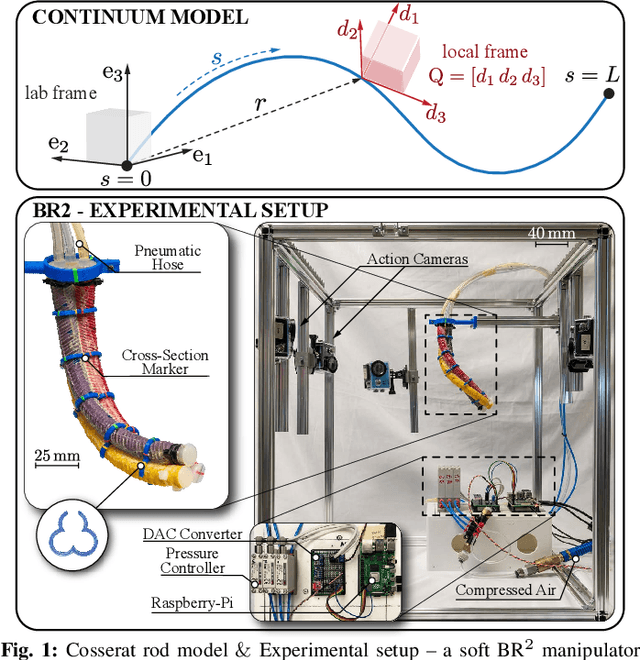
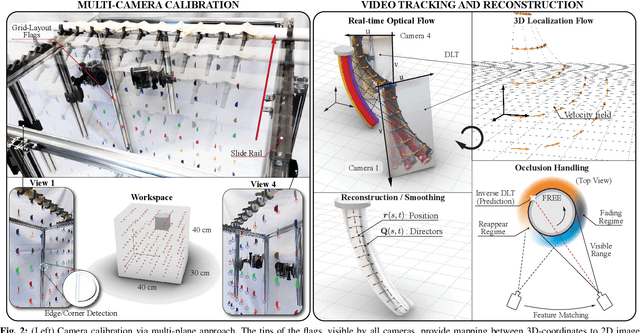
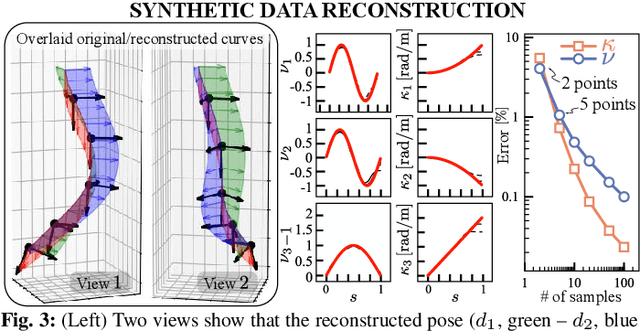
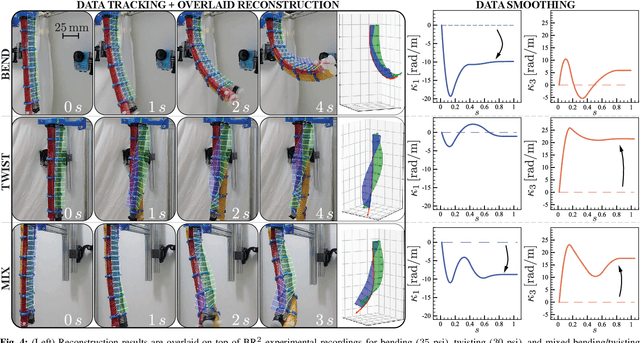
This paper is concerned with the problem of estimating (interpolating and smoothing) the shape (pose and the six modes of deformation) of a slender flexible body from multiple camera measurements. This problem is important in both biology, where slender, soft, and elastic structures are ubiquitously encountered across species, and in engineering, particularly in the area of soft robotics. The proposed mathematical formulation for shape estimation is physics-informed, based on the use of the special Cosserat rod theory whose equations encode slender body mechanics in the presence of bending, shearing, twisting and stretching. The approach is used to derive numerical algorithms which are experimentally demonstrated for fiber reinforced and cable-driven soft robot arms. These experimental demonstrations show that the methodology is accurate (<5 mm error, three times less than the arm diameter) and robust to noise and uncertainties.

Energy Shaping Control of a CyberOctopus Soft Arm

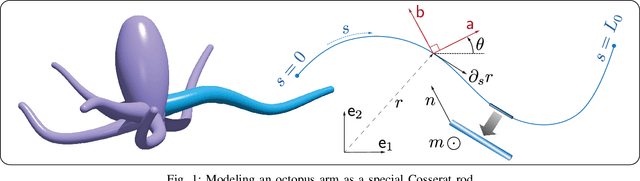
This paper entails application of the energy shaping methodology to control a flexible, elastic Cosserat rod model. Recent interest in such continuum models stems from applications in soft robotics, and from the growing recognition of the role of mechanics and embodiment in biological control strategies: octopuses are often regarded as iconic examples of this interplay. Here, the dynamics of the Cosserat rod, modeling a single octopus arm, are treated as a Hamiltonian system and the internal muscle actuators are modeled as distributed forces and couples. The proposed energy shaping control design procedure involves two steps: (1) a potential energy is designed such that its minimizer is the desired equilibrium configuration; (2) an energy shaping control law is implemented to reach the desired equilibrium. By interpreting the controlled Hamiltonian as a Lyapunov function, asymptotic stability of the equilibrium configuration is deduced. The energy shaping control law is shown to require only the deformations of the equilibrium configuration. A forward-backward algorithm is proposed to compute these deformations in an online iterative manner. The overall control design methodology is implemented and demonstrated in a dynamic simulation environment. Results of several bio-inspired numerical experiments involving the control of octopus arms are reported.