A physics-informed, vision-based method to reconstruct all deformation modes in slender bodies
Paper and Code
Sep 17, 2021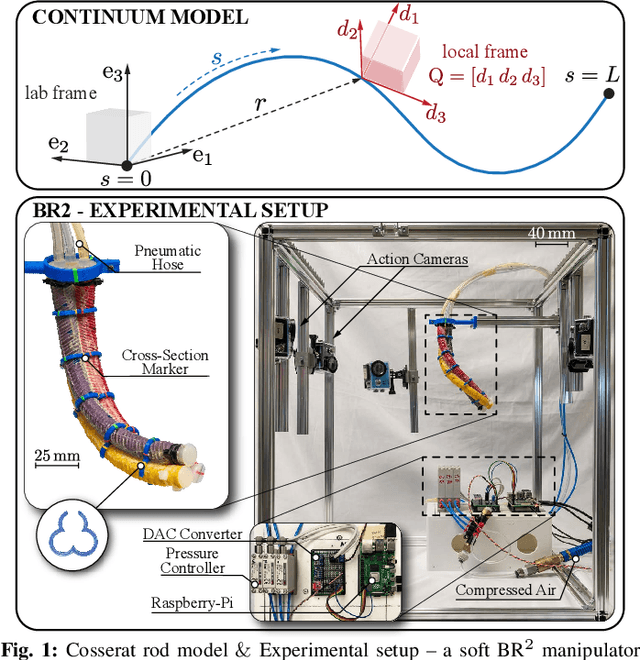
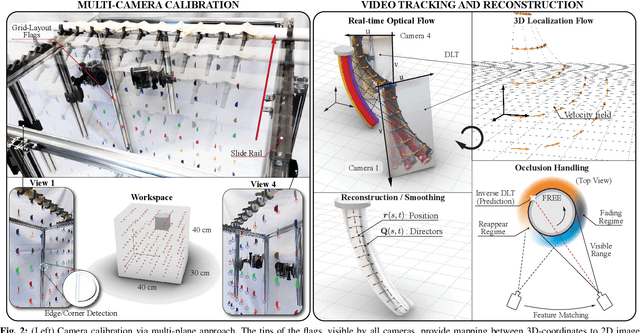
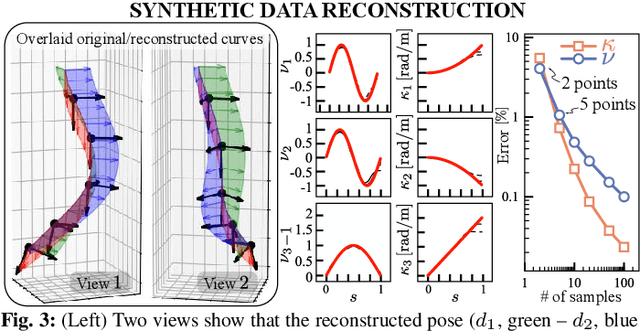
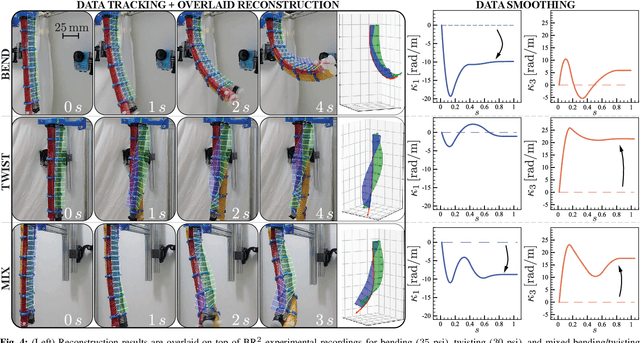
This paper is concerned with the problem of estimating (interpolating and smoothing) the shape (pose and the six modes of deformation) of a slender flexible body from multiple camera measurements. This problem is important in both biology, where slender, soft, and elastic structures are ubiquitously encountered across species, and in engineering, particularly in the area of soft robotics. The proposed mathematical formulation for shape estimation is physics-informed, based on the use of the special Cosserat rod theory whose equations encode slender body mechanics in the presence of bending, shearing, twisting and stretching. The approach is used to derive numerical algorithms which are experimentally demonstrated for fiber reinforced and cable-driven soft robot arms. These experimental demonstrations show that the methodology is accurate (<5 mm error, three times less than the arm diameter) and robust to noise and uncertainties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge