Q-learning with Uniformly Bounded Variance: Large Discounting is Not a Barrier to Fast Learning
Paper and Code
Feb 24, 2020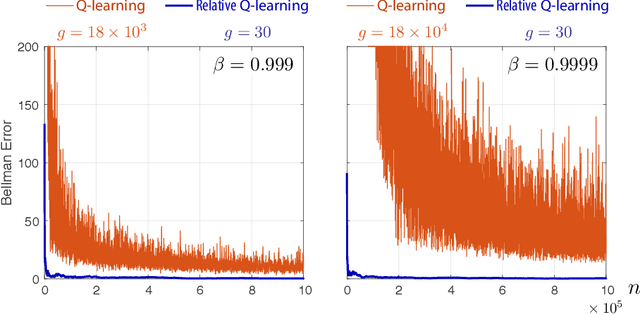
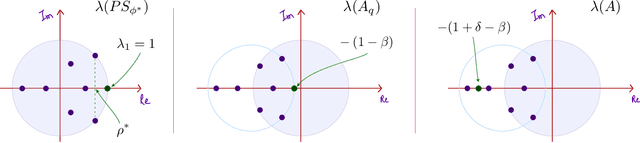
It has been a trend in the Reinforcement Learning literature to derive sample complexity bounds: a bound on how many experiences with the environment are required to obtain an $\varepsilon$-optimal policy. In the discounted cost, infinite horizon setting, all of the known bounds have a factor that is a polynomial in $1/(1-\beta)$, where $\beta < 1$ is the discount factor. For a large discount factor, these bounds seem to imply that a very large number of samples is required to achieve an $\varepsilon$-optimal policy. The objective of the present work is to introduce a new class of algorithms that have sample complexity uniformly bounded for all $\beta < 1$. One may argue that this is impossible, due to a recent min-max lower bound. The explanation is that this previous lower bound is for a specific problem, which we modify, without compromising the ultimate objective of obtaining an $\varepsilon$-optimal policy. Specifically, we show that the asymptotic variance of the Q-learning algorithm, with an optimized step-size sequence, is a quadratic function of $1/(1-\beta)$; an expected, and essentially known result. The new relative Q-learning algorithm proposed here is shown to have asymptotic variance that is a quadratic in $1/(1- \rho \beta)$, where $1 - \rho > 0$ is the spectral gap of an optimal transition matrix.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge