USP: an independence test that improves on Pearson's chi-squared and the $G$-test

We present the $U$-Statistic Permutation (USP) test of independence in the context of discrete data displayed in a contingency table. Either Pearson's chi-squared test of independence, or the $G$-test, are typically used for this task, but we argue that these tests have serious deficiencies, both in terms of their inability to control the size of the test, and their power properties. By contrast, the USP test is guaranteed to control the size of the test at the nominal level for all sample sizes, has no issues with small (or zero) cell counts, and is able to detect distributions that violate independence in only a minimal way. The test statistic is derived from a $U$-statistic estimator of a natural population measure of dependence, and we prove that this is the unique minimum variance unbiased estimator of this population quantity. The practical utility of the USP test is demonstrated on both simulated data, where its power can be dramatically greater than those of Pearson's test and the $G$-test, and on real data. The USP test is implemented in the R package USP.

Locally private non-asymptotic testing of discrete distributions is faster using interactive mechanisms

We find separation rates for testing multinomial or more general discrete distributions under the constraint of local differential privacy. We construct efficient randomized algorithms and test procedures, in both the case where only non-interactive privacy mechanisms are allowed and also in the case where all sequentially interactive privacy mechanisms are allowed. The separation rates are faster in the latter case. We prove general information theoretical bounds that allow us to establish the optimality of our algorithms among all pairs of privacy mechanisms and test procedures, in most usual cases. Considered examples include testing uniform, polynomially and exponentially decreasing distributions.

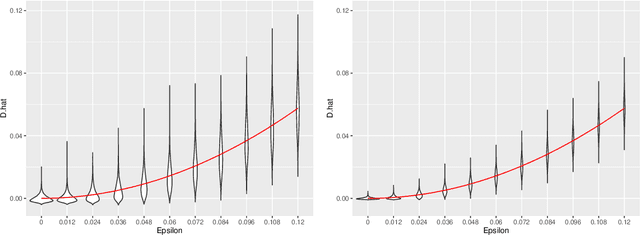
Optimal rates for independence testing via $U$-statistic permutation tests

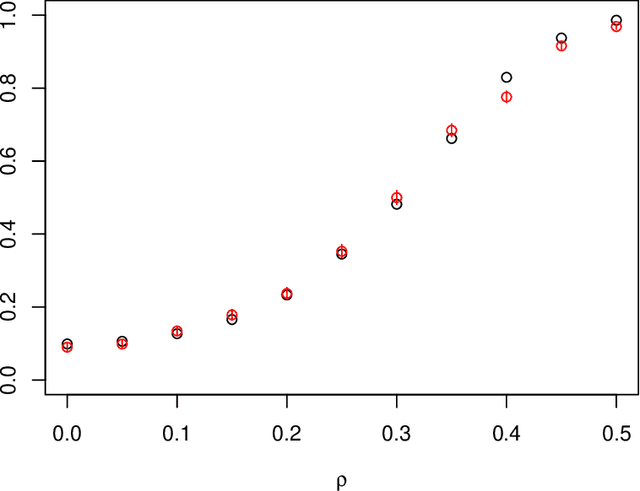
We study the problem of independence testing given independent and identically distributed pairs taking values in a $\sigma$-finite, separable measure space. Defining a natural measure of dependence $D(f)$ as the squared $L_2$-distance between a joint density $f$ and the product of its marginals, we first show that there is no valid test of independence that is uniformly consistent against alternatives of the form $\{f: D(f) \geq \rho^2 \}$. We therefore restrict attention to alternatives that impose additional Sobolev-type smoothness constraints, and define a permutation test based on a basis expansion and a $U$-statistic estimator of $D(f)$ that we prove is minimax optimal in terms of its separation rates in many instances. Finally, for the case of a Fourier basis on $[0,1]^2$, we provide an approximation to the power function that offers several additional insights.

Efficient two-sample functional estimation and the super-oracle phenomenon

We consider the estimation of two-sample integral functionals, of the type that occur naturally, for example, when the object of interest is a divergence between unknown probability densities. Our first main result is that, in wide generality, a weighted nearest neighbour estimator is efficient, in the sense of achieving the local asymptotic minimax lower bound. Moreover, we also prove a corresponding central limit theorem, which facilitates the construction of asymptotically valid confidence intervals for the functional, having asymptotically minimal width. One interesting consequence of our results is the discovery that, for certain functionals, the worst-case performance of our estimator may improve on that of the natural `oracle' estimator, which is given access to the values of the unknown densities at the observations.

Local nearest neighbour classification with applications to semi-supervised learning

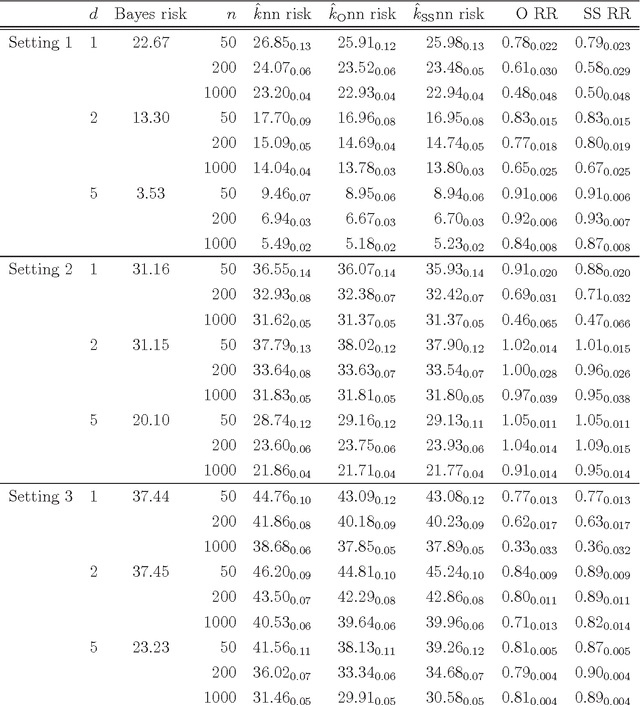
We derive a new asymptotic expansion for the global excess risk of a local $k$-nearest neighbour classifier, where the choice of $k$ may depend upon the test point. This expansion elucidates conditions under which the dominant contribution to the excess risk comes from the locus of points at which each class label is equally likely to occur, but we also show that if these conditions are not satisfied, the dominant contribution may arise from the tails of the marginal distribution of the features. Moreover, we prove that, provided the $d$-dimensional marginal distribution of the features has a finite $\rho$th moment for some $\rho > 4$ (as well as other regularity conditions), a local choice of $k$ can yield a rate of convergence of the excess risk of $O(n^{-4/(d+4)})$, where $n$ is the sample size, whereas for the standard $k$-nearest neighbour classifier, our theory would require $d \geq 5$ and $\rho > 4d/(d-4)$ finite moments to achieve this rate. Our results motivate a new $k$-nearest neighbour classifier for semi-supervised learning problems, where the unlabelled data are used to obtain an estimate of the marginal feature density, and fewer neighbours are used for classification when this density estimate is small. The potential improvements over the standard $k$-nearest neighbour classifier are illustrated both through our theory and via a simulation study.

Nonparametric independence testing via mutual information

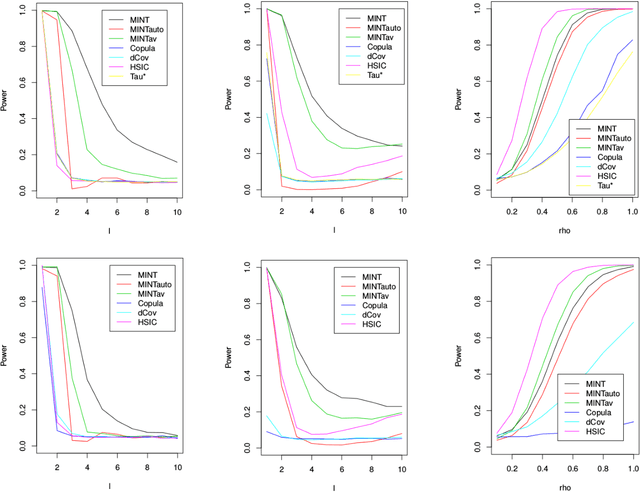
We propose a test of independence of two multivariate random vectors, given a sample from the underlying population. Our approach, which we call MINT, is based on the estimation of mutual information, whose decomposition into joint and marginal entropies facilitates the use of recently-developed efficient entropy estimators derived from nearest neighbour distances. The proposed critical values, which may be obtained from simulation (in the case where one marginal is known) or resampling, guarantee that the test has nominal size, and we provide local power analyses, uniformly over classes of densities whose mutual information satisfies a lower bound. Our ideas may be extended to provide a new goodness-of-fit tests of normal linear models based on assessing the independence of our vector of covariates and an appropriately-defined notion of an error vector. The theory is supported by numerical studies on both simulated and real data.