AMUSE: Adaptive Model Updating using a Simulated Environment

Prediction models frequently face the challenge of concept drift, in which the underlying data distribution changes over time, weakening performance. Examples can include models which predict loan default, or those used in healthcare contexts. Typical management strategies involve regular model updates or updates triggered by concept drift detection. However, these simple policies do not necessarily balance the cost of model updating with improved classifier performance. We present AMUSE (Adaptive Model Updating using a Simulated Environment), a novel method leveraging reinforcement learning trained within a simulated data generating environment, to determine update timings for classifiers. The optimal updating policy depends on the current data generating process and ongoing drift process. Our key idea is that we can train an arbitrarily complex model updating policy by creating a training environment in which possible episodes of drift are simulated by a parametric model, which represents expectations of possible drift patterns. As a result, AMUSE proactively recommends updates based on estimated performance improvements, learning a policy that balances maintaining model performance with minimizing update costs. Empirical results confirm the effectiveness of AMUSE in simulated data.

Random-projection ensemble dimension reduction

We introduce a new framework for dimension reduction in the context of high-dimensional regression. Our proposal is to aggregate an ensemble of random projections, which have been carefully chosen based on the empirical regression performance after being applied to the covariates. More precisely, we consider disjoint groups of independent random projections, apply a base regression method after each projection, and retain the projection in each group based on the empirical performance. We aggregate the selected projections by taking the singular value decomposition of their empirical average and then output the leading order singular vectors. A particularly appealing aspect of our approach is that the singular values provide a measure of the relative importance of the corresponding projection directions, which can be used to select the final projection dimension. We investigate in detail (and provide default recommendations for) various aspects of our general framework, including the projection distribution and the base regression method, as well as the number of random projections used. Additionally, we investigate the possibility of further reducing the dimension by applying our algorithm twice in cases where projection dimension recommended in the initial application is too large. Our theoretical results show that the error of our algorithm stabilises as the number of groups of projections increases. We demonstrate the excellent empirical performance of our proposal in a large numerical study using simulated and real data.

Optimal subgroup selection

In clinical trials and other applications, we often see regions of the feature space that appear to exhibit interesting behaviour, but it is unclear whether these observed phenomena are reflected at the population level. Focusing on a regression setting, we consider the subgroup selection challenge of identifying a region of the feature space on which the regression function exceeds a pre-determined threshold. We formulate the problem as one of constrained optimisation, where we seek a low-complexity, data-dependent selection set on which, with a guaranteed probability, the regression function is uniformly at least as large as the threshold; subject to this constraint, we would like the region to contain as much mass under the marginal feature distribution as possible. This leads to a natural notion of regret, and our main contribution is to determine the minimax optimal rate for this regret in both the sample size and the Type I error probability. The rate involves a delicate interplay between parameters that control the smoothness of the regression function, as well as exponents that quantify the extent to which the optimal selection set at the population level can be approximated by families of well-behaved subsets. Finally, we expand the scope of our previous results by illustrating how they may be generalised to a treatment and control setting, where interest lies in the heterogeneous treatment effect.

Adaptive transfer learning

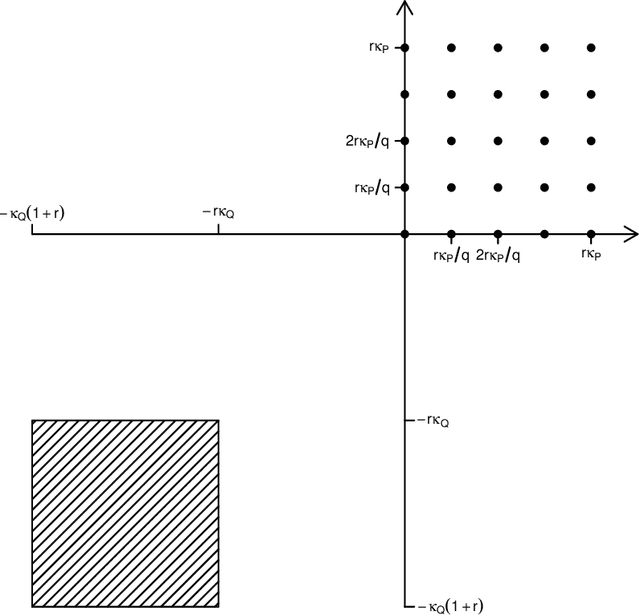
In transfer learning, we wish to make inference about a target population when we have access to data both from the distribution itself, and from a different but related source distribution. We introduce a flexible framework for transfer learning in the context of binary classification, allowing for covariate-dependent relationships between the source and target distributions that are not required to preserve the Bayes decision boundary. Our main contributions are to derive the minimax optimal rates of convergence (up to poly-logarithmic factors) in this problem, and show that the optimal rate can be achieved by an algorithm that adapts to key aspects of the unknown transfer relationship, as well as the smoothness and tail parameters of our distributional classes. This optimal rate turns out to have several regimes, depending on the interplay between the relative sample sizes and the strength of the transfer relationship, and our algorithm achieves optimality by careful, decision tree-based calibration of local nearest-neighbour procedures.

Random projections: data perturbation for classification problems

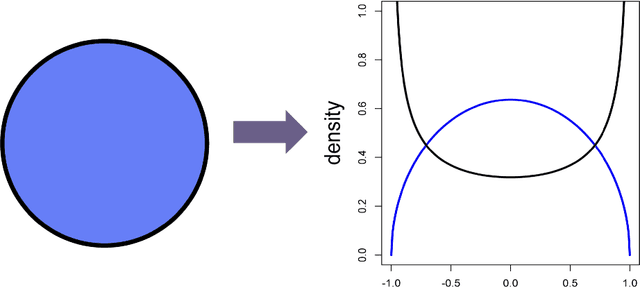
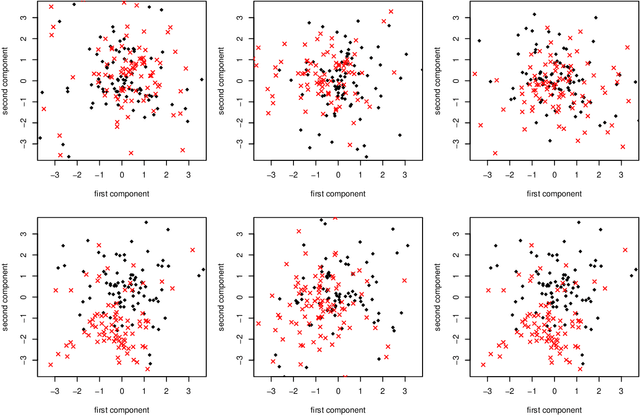
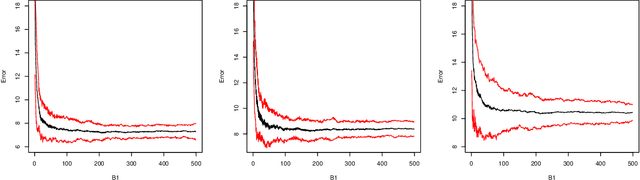
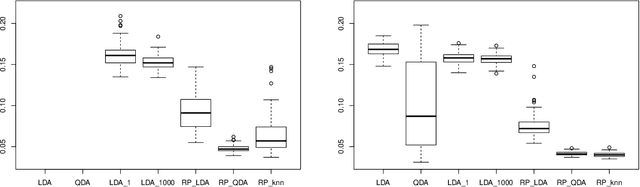
Random projections offer an appealing and flexible approach to a wide range of large-scale statistical problems. They are particularly useful in high-dimensional settings, where we have many covariates recorded for each observation. In classification problems there are two general techniques using random projections. The first involves many projections in an ensemble -- the idea here is to aggregate the results after applying different random projections, with the aim of achieving superior statistical accuracy. The second class of methods include hashing and sketching techniques, which are straightforward ways to reduce the complexity of a problem, perhaps therefore with a huge computational saving, while approximately preserving the statistical efficiency.

Classification with imperfect training labels

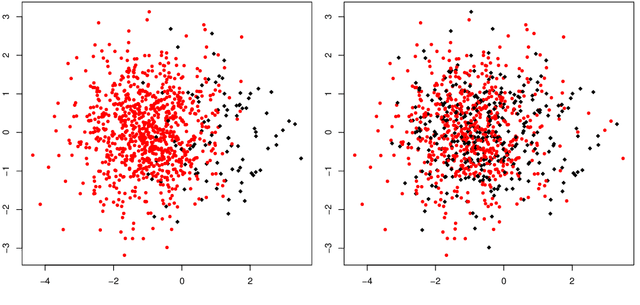
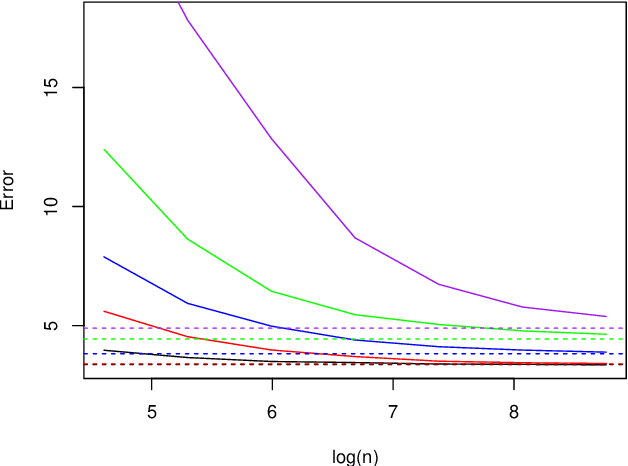
We study the effect of imperfect training data labels on the performance of classification methods. In a general setting, where the probability that an observation in the training dataset is mislabelled may depend on both the feature vector and the true label, we bound the excess risk of an arbitrary classifier trained with imperfect labels in terms of its excess risk for predicting a noisy label. This reveals conditions under which a classifier trained with imperfect labels remains consistent for classifying uncorrupted test data points. Furthermore, under stronger conditions, we derive detailed asymptotic properties for the popular $k$-nearest neighbour ($k$nn), support vector machine (SVM) and linear discriminant analysis (LDA) classifiers. One consequence of these results is that the knn and SVM classifiers are robust to imperfect training labels, in the sense that the rate of convergence of the excess risks of these classifiers remains unchanged; in fact, our theoretical and empirical results even show that in some cases, imperfect labels may improve the performance of these methods. On the other hand, the LDA classifier is shown to be typically inconsistent in the presence of label noise unless the prior probabilities of each class are equal. Our theoretical results are supported by a simulation study.

Local nearest neighbour classification with applications to semi-supervised learning

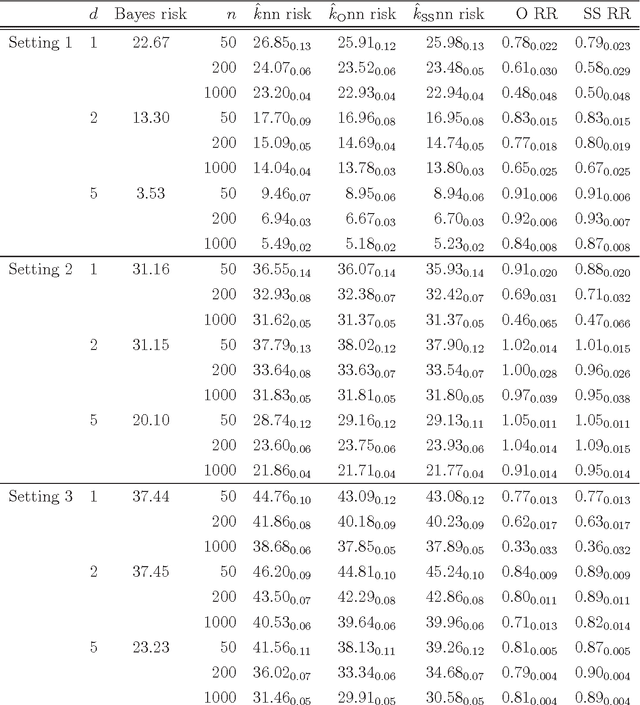
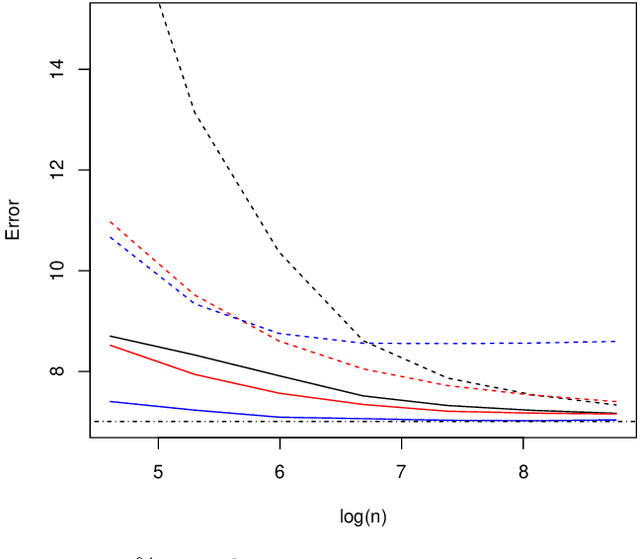
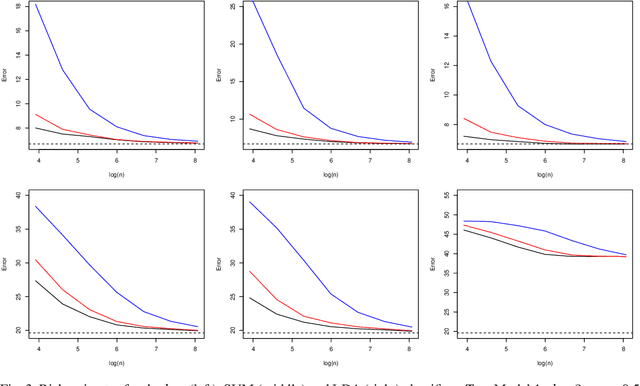
We derive a new asymptotic expansion for the global excess risk of a local $k$-nearest neighbour classifier, where the choice of $k$ may depend upon the test point. This expansion elucidates conditions under which the dominant contribution to the excess risk comes from the locus of points at which each class label is equally likely to occur, but we also show that if these conditions are not satisfied, the dominant contribution may arise from the tails of the marginal distribution of the features. Moreover, we prove that, provided the $d$-dimensional marginal distribution of the features has a finite $\rho$th moment for some $\rho > 4$ (as well as other regularity conditions), a local choice of $k$ can yield a rate of convergence of the excess risk of $O(n^{-4/(d+4)})$, where $n$ is the sample size, whereas for the standard $k$-nearest neighbour classifier, our theory would require $d \geq 5$ and $\rho > 4d/(d-4)$ finite moments to achieve this rate. Our results motivate a new $k$-nearest neighbour classifier for semi-supervised learning problems, where the unlabelled data are used to obtain an estimate of the marginal feature density, and fewer neighbours are used for classification when this density estimate is small. The potential improvements over the standard $k$-nearest neighbour classifier are illustrated both through our theory and via a simulation study.