LLM-Powered CPI Prediction Inference with Online Text Time Series

Forecasting the Consumer Price Index (CPI) is an important yet challenging task in economics, where most existing approaches rely on low-frequency, survey-based data. With the recent advances of large language models (LLMs), there is growing potential to leverage high-frequency online text data for improved CPI prediction, an area still largely unexplored. This paper proposes LLM-CPI, an LLM-based approach for CPI prediction inference incorporating online text time series. We collect a large set of high-frequency online texts from a popularly used Chinese social network site and employ LLMs such as ChatGPT and the trained BERT models to construct continuous inflation labels for posts that are related to inflation. Online text embeddings are extracted via LDA and BERT. We develop a joint time series framework that combines monthly CPI data with LLM-generated daily CPI surrogates. The monthly model employs an ARX structure combining observed CPI data with text embeddings and macroeconomic variables, while the daily model uses a VARX structure built on LLM-generated CPI surrogates and text embeddings. We establish the asymptotic properties of the method and provide two forms of constructed prediction intervals. The finite-sample performance and practical advantages of LLM-CPI are demonstrated through both simulation and real data examples.

Knockoffs Inference under Privacy Constraints

Model-X knockoff framework offers a model-free variable selection method that ensures finite sample false discovery rate (FDR) control. However, the complexity of generating knockoff variables, coupled with the model-free assumption, presents significant challenges for protecting data privacy in this context. In this paper, we propose a comprehensive framework for knockoff inference within the differential privacy paradigm. Our proposed method guarantees robust privacy protection while preserving the exact FDR control entailed by the original model-X knockoff procedure. We further conduct power analysis and establish sufficient conditions under which the noise added for privacy preservation does not asymptotically compromise power. Through various applications, we demonstrate that the differential privacy knockoff (DP-knockoff) method can be effectively utilized to safeguard privacy during variable selection with FDR control in both low and high dimensional settings.

Asymptotic FDR Control with Model-X Knockoffs: Is Moments Matching Sufficient?

We propose a unified theoretical framework for studying the robustness of the model-X knockoffs framework by investigating the asymptotic false discovery rate (FDR) control of the practically implemented approximate knockoffs procedure. This procedure deviates from the model-X knockoffs framework by substituting the true covariate distribution with a user-specified distribution that can be learned using in-sample observations. By replacing the distributional exchangeability condition of the model-X knockoff variables with three conditions on the approximate knockoff statistics, we establish that the approximate knockoffs procedure achieves the asymptotic FDR control. Using our unified framework, we further prove that an arguably most popularly used knockoff variable generation method--the Gaussian knockoffs generator based on the first two moments matching--achieves the asymptotic FDR control when the two-moment-based knockoff statistics are employed in the knockoffs inference procedure. For the first time in the literature, our theoretical results justify formally the effectiveness and robustness of the Gaussian knockoffs generator. Simulation and real data examples are conducted to validate the theoretical findings.

HNCI: High-Dimensional Network Causal Inference

The problem of evaluating the effectiveness of a treatment or policy commonly appears in causal inference applications under network interference. In this paper, we suggest the new method of high-dimensional network causal inference (HNCI) that provides both valid confidence interval on the average direct treatment effect on the treated (ADET) and valid confidence set for the neighborhood size for interference effect. We exploit the model setting in Belloni et al. (2022) and allow certain type of heterogeneity in node interference neighborhood sizes. We propose a linear regression formulation of potential outcomes, where the regression coefficients correspond to the underlying true interference function values of nodes and exhibit a latent homogeneous structure. Such a formulation allows us to leverage existing literature from linear regression and homogeneity pursuit to conduct valid statistical inferences with theoretical guarantees. The resulting confidence intervals for the ADET are formally justified through asymptotic normalities with estimable variances. We further provide the confidence set for the neighborhood size with theoretical guarantees exploiting the repro samples approach. The practical utilities of the newly suggested methods are demonstrated through simulation and real data examples.

Exogenous Randomness Empowering Random Forests

We offer theoretical and empirical insights into the impact of exogenous randomness on the effectiveness of random forests with tree-building rules independent of training data. We formally introduce the concept of exogenous randomness and identify two types of commonly existing randomness: Type I from feature subsampling, and Type II from tie-breaking in tree-building processes. We develop non-asymptotic expansions for the mean squared error (MSE) for both individual trees and forests and establish sufficient and necessary conditions for their consistency. In the special example of the linear regression model with independent features, our MSE expansions are more explicit, providing more understanding of the random forests' mechanisms. It also allows us to derive an upper bound on the MSE with explicit consistency rates for trees and forests. Guided by our theoretical findings, we conduct simulations to further explore how exogenous randomness enhances random forest performance. Our findings unveil that feature subsampling reduces both the bias and variance of random forests compared to individual trees, serving as an adaptive mechanism to balance bias and variance. Furthermore, our results reveal an intriguing phenomenon: the presence of noise features can act as a "blessing" in enhancing the performance of random forests thanks to feature subsampling.

DeepLINK-T: deep learning inference for time series data using knockoffs and LSTM

High-dimensional longitudinal time series data is prevalent across various real-world applications. Many such applications can be modeled as regression problems with high-dimensional time series covariates. Deep learning has been a popular and powerful tool for fitting these regression models. Yet, the development of interpretable and reproducible deep-learning models is challenging and remains underexplored. This study introduces a novel method, Deep Learning Inference using Knockoffs for Time series data (DeepLINK-T), focusing on the selection of significant time series variables in regression while controlling the false discovery rate (FDR) at a predetermined level. DeepLINK-T combines deep learning with knockoff inference to control FDR in feature selection for time series models, accommodating a wide variety of feature distributions. It addresses dependencies across time and features by leveraging a time-varying latent factor structure in time series covariates. Three key ingredients for DeepLINK-T are 1) a Long Short-Term Memory (LSTM) autoencoder for generating time series knockoff variables, 2) an LSTM prediction network using both original and knockoff variables, and 3) the application of the knockoffs framework for variable selection with FDR control. Extensive simulation studies have been conducted to evaluate DeepLINK-T's performance, showing its capability to control FDR effectively while demonstrating superior feature selection power for high-dimensional longitudinal time series data compared to its non-time series counterpart. DeepLINK-T is further applied to three metagenomic data sets, validating its practical utility and effectiveness, and underscoring its potential in real-world applications.

SOFARI: High-Dimensional Manifold-Based Inference

Multi-task learning is a widely used technique for harnessing information from various tasks. Recently, the sparse orthogonal factor regression (SOFAR) framework, based on the sparse singular value decomposition (SVD) within the coefficient matrix, was introduced for interpretable multi-task learning, enabling the discovery of meaningful latent feature-response association networks across different layers. However, conducting precise inference on the latent factor matrices has remained challenging due to orthogonality constraints inherited from the sparse SVD constraint. In this paper, we suggest a novel approach called high-dimensional manifold-based SOFAR inference (SOFARI), drawing on the Neyman near-orthogonality inference while incorporating the Stiefel manifold structure imposed by the SVD constraints. By leveraging the underlying Stiefel manifold structure, SOFARI provides bias-corrected estimators for both latent left factor vectors and singular values, for which we show to enjoy the asymptotic mean-zero normal distributions with estimable variances. We introduce two SOFARI variants to handle strongly and weakly orthogonal latent factors, where the latter covers a broader range of applications. We illustrate the effectiveness of SOFARI and justify our theoretical results through simulation examples and a real data application in economic forecasting.

ARK: Robust Knockoffs Inference with Coupling

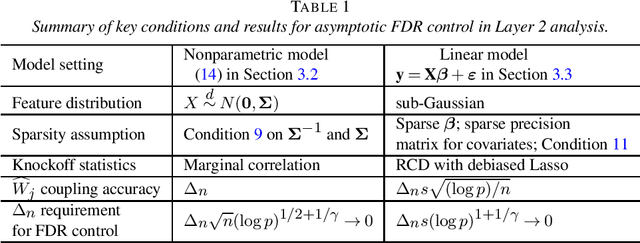
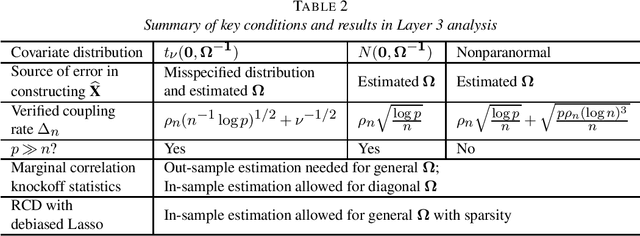
We investigate the robustness of the model-X knockoffs framework with respect to the misspecified or estimated feature distribution. We achieve such a goal by theoretically studying the feature selection performance of a practically implemented knockoffs algorithm, which we name as the approximate knockoffs (ARK) procedure, under the measures of the false discovery rate (FDR) and family wise error rate (FWER). The approximate knockoffs procedure differs from the model-X knockoffs procedure only in that the former uses the misspecified or estimated feature distribution. A key technique in our theoretical analyses is to couple the approximate knockoffs procedure with the model-X knockoffs procedure so that random variables in these two procedures can be close in realizations. We prove that if such coupled model-X knockoffs procedure exists, the approximate knockoffs procedure can achieve the asymptotic FDR or FWER control at the target level. We showcase three specific constructions of such coupled model-X knockoff variables, verifying their existence and justifying the robustness of the model-X knockoffs framework.

BrainNet: Epileptic Wave Detection from SEEG with Hierarchical Graph Diffusion Learning

Epilepsy is one of the most serious neurological diseases, affecting 1-2% of the world's population. The diagnosis of epilepsy depends heavily on the recognition of epileptic waves, i.e., disordered electrical brainwave activity in the patient's brain. Existing works have begun to employ machine learning models to detect epileptic waves via cortical electroencephalogram (EEG). However, the recently developed stereoelectrocorticography (SEEG) method provides information in stereo that is more precise than conventional EEG, and has been broadly applied in clinical practice. Therefore, we propose the first data-driven study to detect epileptic waves in a real-world SEEG dataset. While offering new opportunities, SEEG also poses several challenges. In clinical practice, epileptic wave activities are considered to propagate between different regions in the brain. These propagation paths, also known as the epileptogenic network, are deemed to be a key factor in the context of epilepsy surgery. However, the question of how to extract an exact epileptogenic network for each patient remains an open problem in the field of neuroscience. To address these challenges, we propose a novel model (BrainNet) that jointly learns the dynamic diffusion graphs and models the brain wave diffusion patterns. In addition, our model effectively aids in resisting label imbalance and severe noise by employing several self-supervised learning tasks and a hierarchical framework. By experimenting with the extensive real SEEG dataset obtained from multiple patients, we find that BrainNet outperforms several latest state-of-the-art baselines derived from time-series analysis.

Revisit Weakly-Supervised Audio-Visual Video Parsing from the Language Perspective

We focus on the weakly-supervised audio-visual video parsing task (AVVP), which aims to identify and locate all the events in audio/visual modalities. Previous works only concentrate on video-level overall label denoising across modalities, but overlook the segment-level label noise, where adjacent video segments (i.e., 1-second video clips) may contain different events. However, recognizing events in the segment is challenging because its label could be any combination of events that occur in the video. To address this issue, we consider tackling AVVP from the language perspective, since language could freely describe how various events appear in each segment beyond fixed labels. Specifically, we design language prompts to describe all cases of event appearance for each video. Then, the similarity between language prompts and segments is calculated, where the event of the most similar prompt is regarded as the segment-level label. In addition, to deal with the mislabeled segments, we propose to perform dynamic re-weighting on the unreliable segments to adjust their labels. Experiments show that our simple yet effective approach outperforms state-of-the-art methods by a large margin.