Sample-efficient quantum error mitigation via classical learning surrogates

The pursuit of practical quantum utility on near-term quantum processors is critically challenged by their inherent noise. Quantum error mitigation (QEM) techniques are leading solutions to improve computation fidelity with relatively low qubit-overhead, while full-scale quantum error correction remains a distant goal. However, QEM techniques incur substantial measurement overheads, especially when applied to families of quantum circuits parameterized by classical inputs. Focusing on zero-noise extrapolation (ZNE), a widely adopted QEM technique, here we devise the surrogate-enabled ZNE (S-ZNE), which leverages classical learning surrogates to perform ZNE entirely on the classical side. Unlike conventional ZNE, whose measurement cost scales linearly with the number of circuits, S-ZNE requires only constant measurement overhead for an entire family of quantum circuits, offering superior scalability. Theoretical analysis indicates that S-ZNE achieves accuracy comparable to conventional ZNE in many practical scenarios, and numerical experiments on up to 100-qubit ground-state energy and quantum metrology tasks confirm its effectiveness. Our approach provides a template that can be effectively extended to other quantum error mitigation protocols, opening a promising path toward scalable error mitigation.

TITAN: A Trajectory-Informed Technique for Adaptive Parameter Freezing in Large-Scale VQE

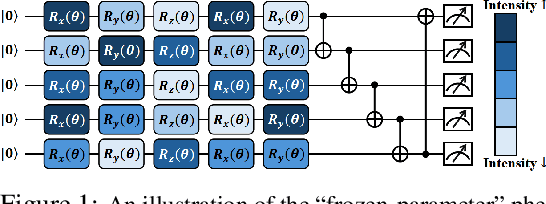
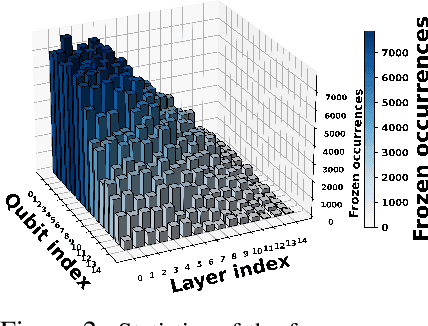
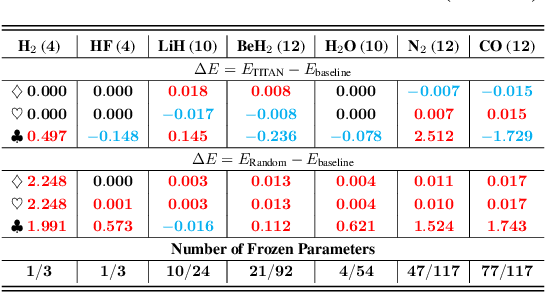
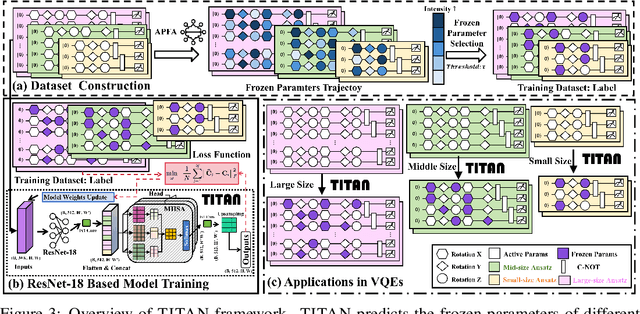
Variational quantum Eigensolver (VQE) is a leading candidate for harnessing quantum computers to advance quantum chemistry and materials simulations, yet its training efficiency deteriorates rapidly for large Hamiltonians. Two issues underlie this bottleneck: (i) the no-cloning theorem imposes a linear growth in circuit evaluations with the number of parameters per gradient step; and (ii) deeper circuits encounter barren plateaus (BPs), leading to exponentially increasing measurement overheads. To address these challenges, here we propose a deep learning framework, dubbed Titan, which identifies and freezes inactive parameters of a given ansatze at initialization for a specific class of Hamiltonians, reducing the optimization overhead without sacrificing accuracy. The motivation of Titan starts with our empirical findings that a subset of parameters consistently has a negligible influence on training dynamics. Its design combines a theoretically grounded data construction strategy, ensuring each training example is informative and BP-resilient, with an adaptive neural architecture that generalizes across ansatze of varying sizes. Across benchmark transverse-field Ising models, Heisenberg models, and multiple molecule systems up to 30 qubits, Titan achieves up to 3 times faster convergence and 40% to 60% fewer circuit evaluations than state-of-the-art baselines, while matching or surpassing their estimation accuracy. By proactively trimming parameter space, Titan lowers hardware demands and offers a scalable path toward utilizing VQE to advance practical quantum chemistry and materials science.

Artificial intelligence for representing and characterizing quantum systems

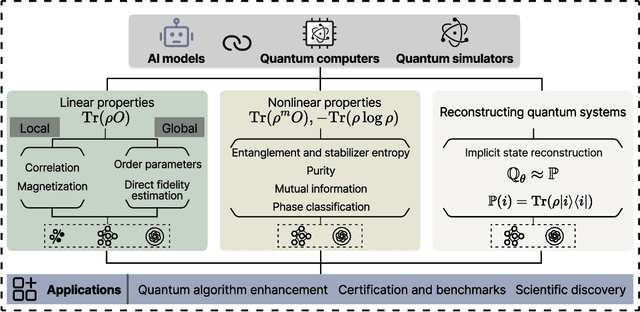
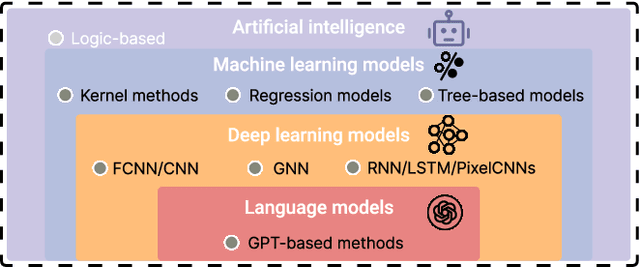
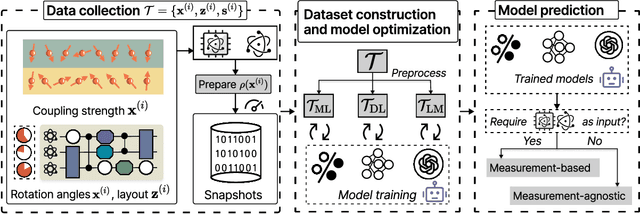
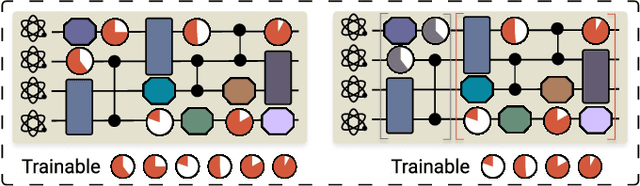
Efficient characterization of large-scale quantum systems, especially those produced by quantum analog simulators and megaquop quantum computers, poses a central challenge in quantum science due to the exponential scaling of the Hilbert space with respect to system size. Recent advances in artificial intelligence (AI), with its aptitude for high-dimensional pattern recognition and function approximation, have emerged as a powerful tool to address this challenge. A growing body of research has leveraged AI to represent and characterize scalable quantum systems, spanning from theoretical foundations to experimental realizations. Depending on how prior knowledge and learning architectures are incorporated, the integration of AI into quantum system characterization can be categorized into three synergistic paradigms: machine learning, and, in particular, deep learning and language models. This review discusses how each of these AI paradigms contributes to two core tasks in quantum systems characterization: quantum property prediction and the construction of surrogates for quantum states. These tasks underlie diverse applications, from quantum certification and benchmarking to the enhancement of quantum algorithms and the understanding of strongly correlated phases of matter. Key challenges and open questions are also discussed, together with future prospects at the interface of AI and quantum science.

Demonstration of Efficient Predictive Surrogates for Large-scale Quantum Processors

The ongoing development of quantum processors is driving breakthroughs in scientific discovery. Despite this progress, the formidable cost of fabricating large-scale quantum processors means they will remain rare for the foreseeable future, limiting their widespread application. To address this bottleneck, we introduce the concept of predictive surrogates, which are classical learning models designed to emulate the mean-value behavior of a given quantum processor with provably computational efficiency. In particular, we propose two predictive surrogates that can substantially reduce the need for quantum processor access in diverse practical scenarios. To demonstrate their potential in advancing digital quantum simulation, we use these surrogates to emulate a quantum processor with up to 20 programmable superconducting qubits, enabling efficient pre-training of variational quantum eigensolvers for families of transverse-field Ising models and identification of non-equilibrium Floquet symmetry-protected topological phases. Experimental results reveal that the predictive surrogates not only reduce measurement overhead by orders of magnitude, but can also surpass the performance of conventional, quantum-resource-intensive approaches. Collectively, these findings establish predictive surrogates as a practical pathway to broadening the impact of advanced quantum processors.

Overlap-Adaptive Hybrid Speaker Diarization and ASR-Aware Observation Addition for MISP 2025 Challenge

This paper presents the system developed to address the MISP 2025 Challenge. For the diarization system, we proposed a hybrid approach combining a WavLM end-to-end segmentation method with a traditional multi-module clustering technique to adaptively select the appropriate model for handling varying degrees of overlapping speech. For the automatic speech recognition (ASR) system, we proposed an ASR-aware observation addition method that compensates for the performance limitations of Guided Source Separation (GSS) under low signal-to-noise ratio conditions. Finally, we integrated the speaker diarization and ASR systems in a cascaded architecture to address Track 3. Our system achieved character error rates (CER) of 9.48% on Track 2 and concatenated minimum permutation character error rate (cpCER) of 11.56% on Track 3, ultimately securing first place in both tracks and thereby demonstrating the effectiveness of the proposed methods in real-world meeting scenarios.

CAD: A General Multimodal Framework for Video Deepfake Detection via Cross-Modal Alignment and Distillation

The rapid emergence of multimodal deepfakes (visual and auditory content are manipulated in concert) undermines the reliability of existing detectors that rely solely on modality-specific artifacts or cross-modal inconsistencies. In this work, we first demonstrate that modality-specific forensic traces (e.g., face-swap artifacts or spectral distortions) and modality-shared semantic misalignments (e.g., lip-speech asynchrony) offer complementary evidence, and that neglecting either aspect limits detection performance. Existing approaches either naively fuse modality-specific features without reconciling their conflicting characteristics or focus predominantly on semantic misalignment at the expense of modality-specific fine-grained artifact cues. To address these shortcomings, we propose a general multimodal framework for video deepfake detection via Cross-Modal Alignment and Distillation (CAD). CAD comprises two core components: 1) Cross-modal alignment that identifies inconsistencies in high-level semantic synchronization (e.g., lip-speech mismatches); 2) Cross-modal distillation that mitigates feature conflicts during fusion while preserving modality-specific forensic traces (e.g., spectral distortions in synthetic audio). Extensive experiments on both multimodal and unimodal (e.g., image-only/video-only)deepfake benchmarks demonstrate that CAD significantly outperforms previous methods, validating the necessity of harmonious integration of multimodal complementary information.

Rethink the Role of Deep Learning towards Large-scale Quantum Systems

Characterizing the ground state properties of quantum systems is fundamental to capturing their behavior but computationally challenging. Recent advances in AI have introduced novel approaches, with diverse machine learning (ML) and deep learning (DL) models proposed for this purpose. However, the necessity and specific role of DL models in these tasks remain unclear, as prior studies often employ varied or impractical quantum resources to construct datasets, resulting in unfair comparisons. To address this, we systematically benchmark DL models against traditional ML approaches across three families of Hamiltonian, scaling up to 127 qubits in three crucial ground-state learning tasks while enforcing equivalent quantum resource usage. Our results reveal that ML models often achieve performance comparable to or even exceeding that of DL approaches across all tasks. Furthermore, a randomization test demonstrates that measurement input features have minimal impact on DL models' prediction performance. These findings challenge the necessity of current DL models in many quantum system learning scenarios and provide valuable insights into their effective utilization.

Quantum Machine Learning: A Hands-on Tutorial for Machine Learning Practitioners and Researchers

This tutorial intends to introduce readers with a background in AI to quantum machine learning (QML) -- a rapidly evolving field that seeks to leverage the power of quantum computers to reshape the landscape of machine learning. For self-consistency, this tutorial covers foundational principles, representative QML algorithms, their potential applications, and critical aspects such as trainability, generalization, and computational complexity. In addition, practical code demonstrations are provided in https://qml-tutorial.github.io/ to illustrate real-world implementations and facilitate hands-on learning. Together, these elements offer readers a comprehensive overview of the latest advancements in QML. By bridging the gap between classical machine learning and quantum computing, this tutorial serves as a valuable resource for those looking to engage with QML and explore the forefront of AI in the quantum era.

MG-Net: Learn to Customize QAOA with Circuit Depth Awareness

Quantum Approximate Optimization Algorithm (QAOA) and its variants exhibit immense potential in tackling combinatorial optimization challenges. However, their practical realization confronts a dilemma: the requisite circuit depth for satisfactory performance is problem-specific and often exceeds the maximum capability of current quantum devices. To address this dilemma, here we first analyze the convergence behavior of QAOA, uncovering the origins of this dilemma and elucidating the intricate relationship between the employed mixer Hamiltonian, the specific problem at hand, and the permissible maximum circuit depth. Harnessing this understanding, we introduce the Mixer Generator Network (MG-Net), a unified deep learning framework adept at dynamically formulating optimal mixer Hamiltonians tailored to distinct tasks and circuit depths. Systematic simulations, encompassing Ising models and weighted Max-Cut instances with up to 64 qubits, substantiate our theoretical findings, highlighting MG-Net's superior performance in terms of both approximation ratio and efficiency.

Efficient Learning for Linear Properties of Bounded-Gate Quantum Circuits

The vast and complicated large-qubit state space forbids us to comprehensively capture the dynamics of modern quantum computers via classical simulations or quantum tomography. However, recent progress in quantum learning theory invokes a crucial question: given a quantum circuit containing d tunable RZ gates and G-d Clifford gates, can a learner perform purely classical inference to efficiently predict its linear properties using new classical inputs, after learning from data obtained by incoherently measuring states generated by the same circuit but with different classical inputs? In this work, we prove that the sample complexity scaling linearly in d is necessary and sufficient to achieve a small prediction error, while the corresponding computational complexity may scale exponentially in d. Building upon these derived complexity bounds, we further harness the concept of classical shadow and truncated trigonometric expansion to devise a kernel-based learning model capable of trading off prediction error and computational complexity, transitioning from exponential to polynomial scaling in many practical settings. Our results advance two crucial realms in quantum computation: the exploration of quantum algorithms with practical utilities and learning-based quantum system certification. We conduct numerical simulations to validate our proposals across diverse scenarios, encompassing quantum information processing protocols, Hamiltonian simulation, and variational quantum algorithms up to 60 qubits.