Separable Power of Classical and Quantum Learning Protocols Through the Lens of No-Free-Lunch Theorem
Paper and Code
May 12, 2024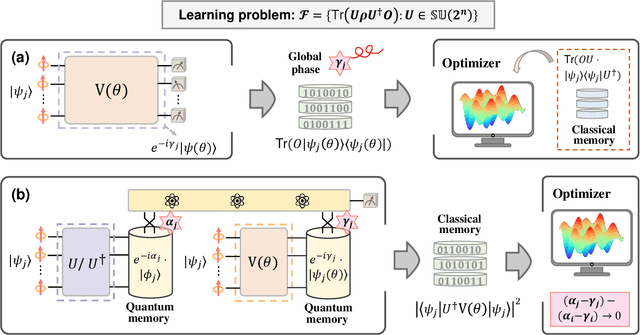
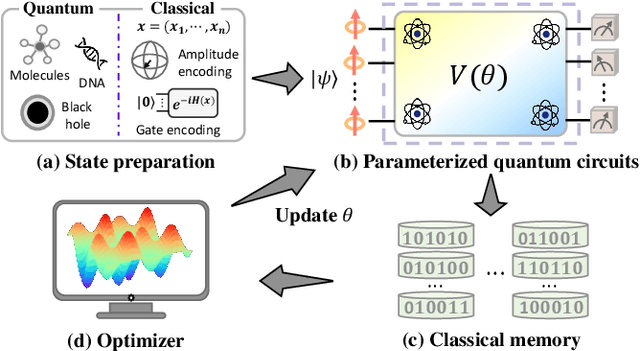
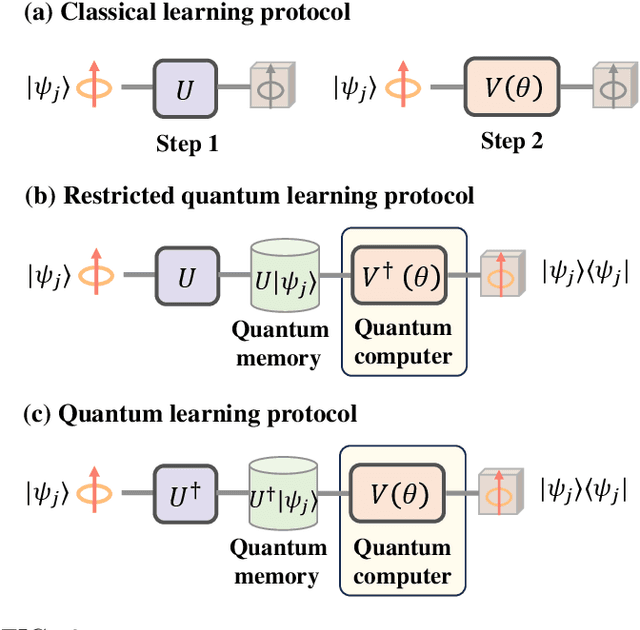
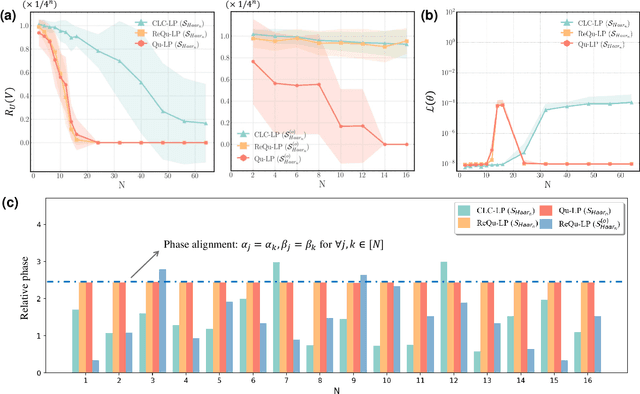
The No-Free-Lunch (NFL) theorem, which quantifies problem- and data-independent generalization errors regardless of the optimization process, provides a foundational framework for comprehending diverse learning protocols' potential. Despite its significance, the establishment of the NFL theorem for quantum machine learning models remains largely unexplored, thereby overlooking broader insights into the fundamental relationship between quantum and classical learning protocols. To address this gap, we categorize a diverse array of quantum learning algorithms into three learning protocols designed for learning quantum dynamics under a specified observable and establish their NFL theorem. The exploited protocols, namely Classical Learning Protocols (CLC-LPs), Restricted Quantum Learning Protocols (ReQu-LPs), and Quantum Learning Protocols (Qu-LPs), offer varying levels of access to quantum resources. Our derived NFL theorems demonstrate quadratic reductions in sample complexity across CLC-LPs, ReQu-LPs, and Qu-LPs, contingent upon the orthogonality of quantum states and the diagonality of observables. We attribute this performance discrepancy to the unique capacity of quantum-related learning protocols to indirectly utilize information concerning the global phases of non-orthogonal quantum states, a distinctive physical feature inherent in quantum mechanics. Our findings not only deepen our understanding of quantum learning protocols' capabilities but also provide practical insights for the development of advanced quantum learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge