MG-Net: Learn to Customize QAOA with Circuit Depth Awareness

Quantum Approximate Optimization Algorithm (QAOA) and its variants exhibit immense potential in tackling combinatorial optimization challenges. However, their practical realization confronts a dilemma: the requisite circuit depth for satisfactory performance is problem-specific and often exceeds the maximum capability of current quantum devices. To address this dilemma, here we first analyze the convergence behavior of QAOA, uncovering the origins of this dilemma and elucidating the intricate relationship between the employed mixer Hamiltonian, the specific problem at hand, and the permissible maximum circuit depth. Harnessing this understanding, we introduce the Mixer Generator Network (MG-Net), a unified deep learning framework adept at dynamically formulating optimal mixer Hamiltonians tailored to distinct tasks and circuit depths. Systematic simulations, encompassing Ising models and weighted Max-Cut instances with up to 64 qubits, substantiate our theoretical findings, highlighting MG-Net's superior performance in terms of both approximation ratio and efficiency.

Separable Power of Classical and Quantum Learning Protocols Through the Lens of No-Free-Lunch Theorem

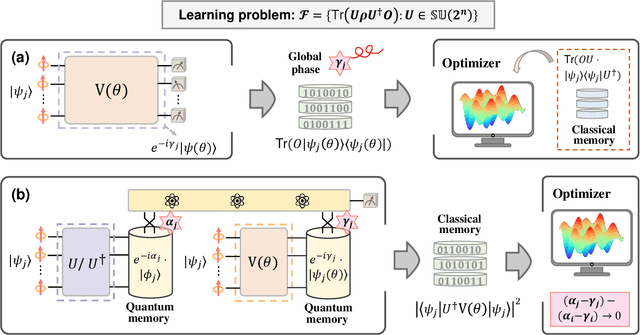
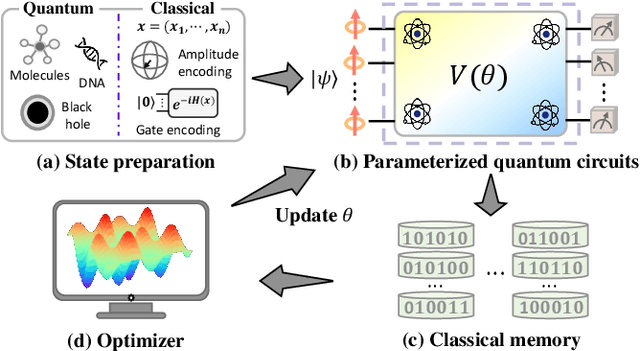
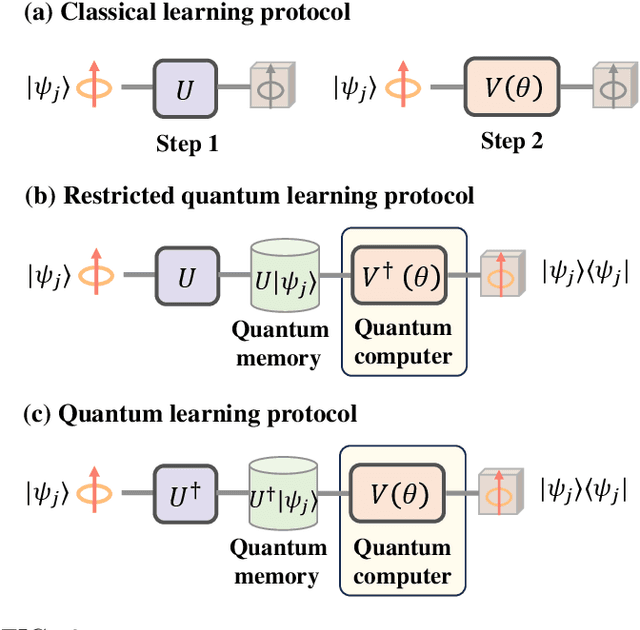
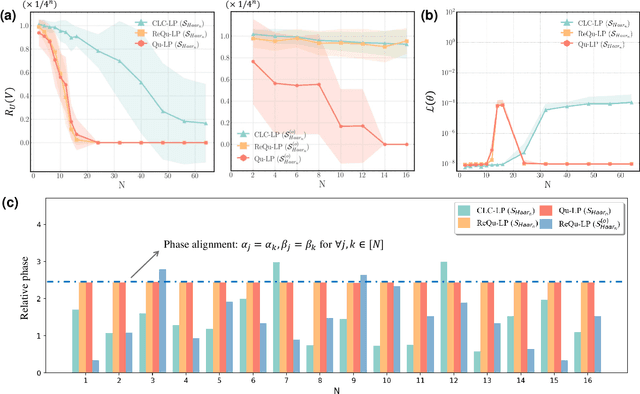
The No-Free-Lunch (NFL) theorem, which quantifies problem- and data-independent generalization errors regardless of the optimization process, provides a foundational framework for comprehending diverse learning protocols' potential. Despite its significance, the establishment of the NFL theorem for quantum machine learning models remains largely unexplored, thereby overlooking broader insights into the fundamental relationship between quantum and classical learning protocols. To address this gap, we categorize a diverse array of quantum learning algorithms into three learning protocols designed for learning quantum dynamics under a specified observable and establish their NFL theorem. The exploited protocols, namely Classical Learning Protocols (CLC-LPs), Restricted Quantum Learning Protocols (ReQu-LPs), and Quantum Learning Protocols (Qu-LPs), offer varying levels of access to quantum resources. Our derived NFL theorems demonstrate quadratic reductions in sample complexity across CLC-LPs, ReQu-LPs, and Qu-LPs, contingent upon the orthogonality of quantum states and the diagonality of observables. We attribute this performance discrepancy to the unique capacity of quantum-related learning protocols to indirectly utilize information concerning the global phases of non-orthogonal quantum states, a distinctive physical feature inherent in quantum mechanics. Our findings not only deepen our understanding of quantum learning protocols' capabilities but also provide practical insights for the development of advanced quantum learning algorithms.

Transition role of entangled data in quantum machine learning

Entanglement serves as the resource to empower quantum computing. Recent progress has highlighted its positive impact on learning quantum dynamics, wherein the integration of entanglement into quantum operations or measurements of quantum machine learning (QML) models leads to substantial reductions in training data size, surpassing a specified prediction error threshold. However, an analytical understanding of how the entanglement degree in data affects model performance remains elusive. In this study, we address this knowledge gap by establishing a quantum no-free-lunch (NFL) theorem for learning quantum dynamics using entangled data. Contrary to previous findings, we prove that the impact of entangled data on prediction error exhibits a dual effect, depending on the number of permitted measurements. With a sufficient number of measurements, increasing the entanglement of training data consistently reduces the prediction error or decreases the required size of the training data to achieve the same prediction error. Conversely, when few measurements are allowed, employing highly entangled data could lead to an increased prediction error. The achieved results provide critical guidance for designing advanced QML protocols, especially for those tailored for execution on early-stage quantum computers with limited access to quantum resources.

Symmetric Pruning in Quantum Neural Networks

Many fundamental properties of a quantum system are captured by its Hamiltonian and ground state. Despite the significance of ground states preparation (GSP), this task is classically intractable for large-scale Hamiltonians. Quantum neural networks (QNNs), which exert the power of modern quantum machines, have emerged as a leading protocol to conquer this issue. As such, how to enhance the performance of QNNs becomes a crucial topic in GSP. Empirical evidence showed that QNNs with handcraft symmetric ansatzes generally experience better trainability than those with asymmetric ansatzes, while theoretical explanations have not been explored. To fill this knowledge gap, here we propose the effective quantum neural tangent kernel (EQNTK) and connect this concept with over-parameterization theory to quantify the convergence of QNNs towards the global optima. We uncover that the advance of symmetric ansatzes attributes to their large EQNTK value with low effective dimension, which requests few parameters and quantum circuit depth to reach the over-parameterization regime permitting a benign loss landscape and fast convergence. Guided by EQNTK, we further devise a symmetric pruning (SP) scheme to automatically tailor a symmetric ansatz from an over-parameterized and asymmetric one to greatly improve the performance of QNNs when the explicit symmetry information of Hamiltonian is unavailable. Extensive numerical simulations are conducted to validate the analytical results of EQNTK and the effectiveness of SP.

The dilemma of quantum neural networks

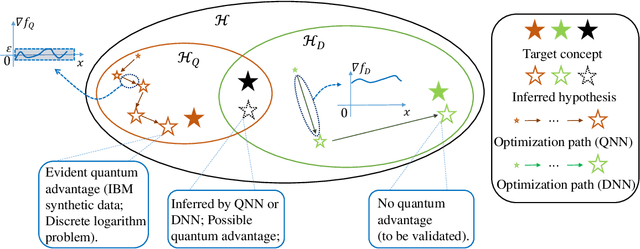
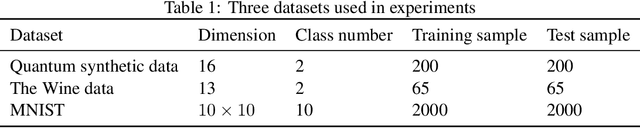
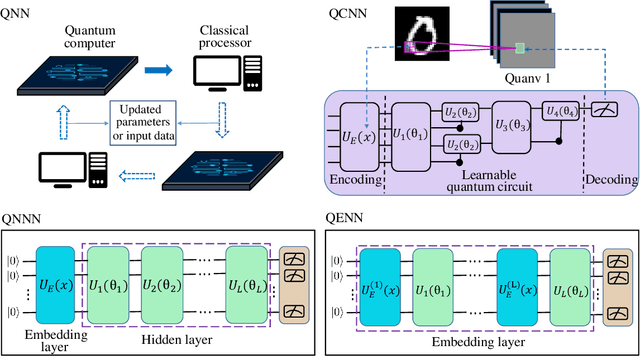
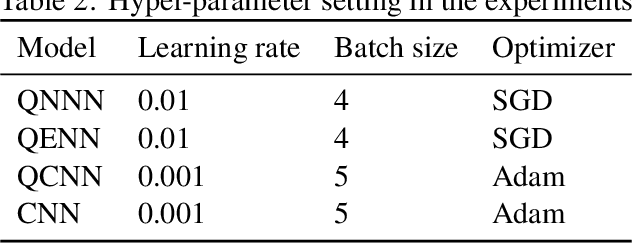
The core of quantum machine learning is to devise quantum models with good trainability and low generalization error bound than their classical counterparts to ensure better reliability and interpretability. Recent studies confirmed that quantum neural networks (QNNs) have the ability to achieve this goal on specific datasets. With this regard, it is of great importance to understand whether these advantages are still preserved on real-world tasks. Through systematic numerical experiments, we empirically observe that current QNNs fail to provide any benefit over classical learning models. Concretely, our results deliver two key messages. First, QNNs suffer from the severely limited effective model capacity, which incurs poor generalization on real-world datasets. Second, the trainability of QNNs is insensitive to regularization techniques, which sharply contrasts with the classical scenario. These empirical results force us to rethink the role of current QNNs and to design novel protocols for solving real-world problems with quantum advantages.

Towards understanding the power of quantum kernels in the NISQ era

A key problem in the field of quantum computing is understanding whether quantum machine learning (QML) models implemented on noisy intermediate-scale quantum (NISQ) machines can achieve quantum advantages. Recently, Huang et al. [arXiv:2011.01938] partially answered this question by the lens of quantum kernel learning. Namely, they exhibited that quantum kernels can learn specific datasets with lower generalization error over the optimal classical kernel methods. However, most of their results are established on the ideal setting and ignore the caveats of near-term quantum machines. To this end, a crucial open question is: does the power of quantum kernels still hold under the NISQ setting? In this study, we fill this knowledge gap by exploiting the power of quantum kernels when the quantum system noise and sample error are considered. Concretely, we first prove that the advantage of quantum kernels is vanished for large size of datasets, few number of measurements, and large system noise. With the aim of preserving the superiority of quantum kernels in the NISQ era, we further devise an effective method via indefinite kernel learning. Numerical simulations accord with our theoretical results. Our work provides theoretical guidance of exploring advanced quantum kernels to attain quantum advantages on NISQ devices.