Quantum Compiling with Reinforcement Learning on a Superconducting Processor

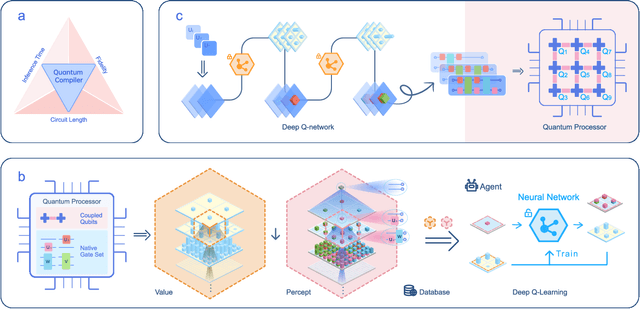
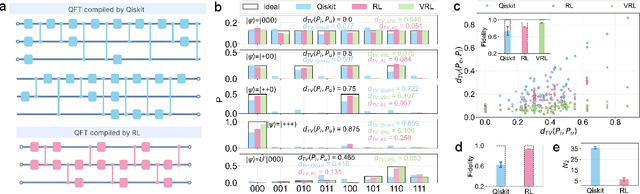
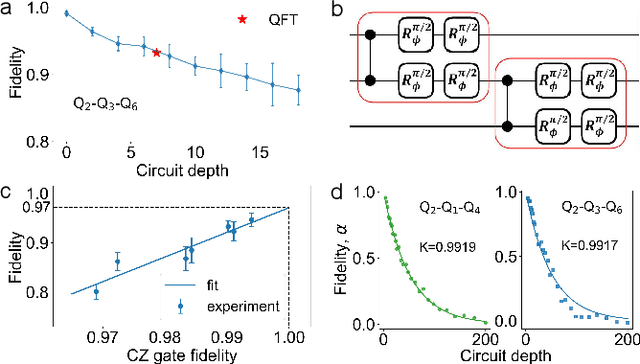
To effectively implement quantum algorithms on noisy intermediate-scale quantum (NISQ) processors is a central task in modern quantum technology. NISQ processors feature tens to a few hundreds of noisy qubits with limited coherence times and gate operations with errors, so NISQ algorithms naturally require employing circuits of short lengths via quantum compilation. Here, we develop a reinforcement learning (RL)-based quantum compiler for a superconducting processor and demonstrate its capability of discovering novel and hardware-amenable circuits with short lengths. We show that for the three-qubit quantum Fourier transformation, a compiled circuit using only seven CZ gates with unity circuit fidelity can be achieved. The compiler is also able to find optimal circuits under device topological constraints, with lengths considerably shorter than those by the conventional method. Our study exemplifies the codesign of the software with hardware for efficient quantum compilation, offering valuable insights for the advancement of RL-based compilers.

Recent Advances for Quantum Neural Networks in Generative Learning

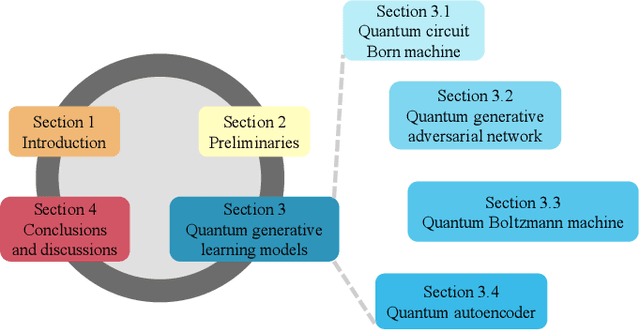
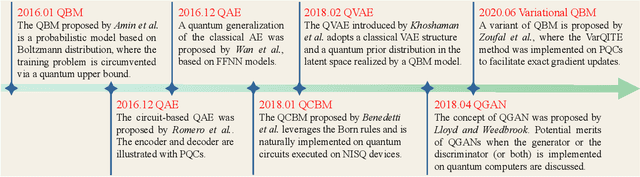
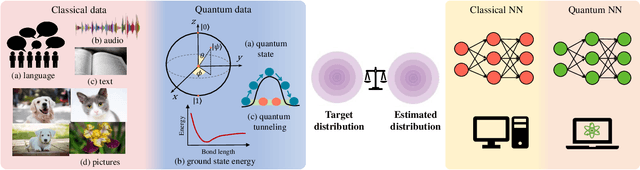
Quantum computers are next-generation devices that hold promise to perform calculations beyond the reach of classical computers. A leading method towards achieving this goal is through quantum machine learning, especially quantum generative learning. Due to the intrinsic probabilistic nature of quantum mechanics, it is reasonable to postulate that quantum generative learning models (QGLMs) may surpass their classical counterparts. As such, QGLMs are receiving growing attention from the quantum physics and computer science communities, where various QGLMs that can be efficiently implemented on near-term quantum machines with potential computational advantages are proposed. In this paper, we review the current progress of QGLMs from the perspective of machine learning. Particularly, we interpret these QGLMs, covering quantum circuit born machines, quantum generative adversarial networks, quantum Boltzmann machines, and quantum autoencoders, as the quantum extension of classical generative learning models. In this context, we explore their intrinsic relation and their fundamental differences. We further summarize the potential applications of QGLMs in both conventional machine learning tasks and quantum physics. Last, we discuss the challenges and further research directions for QGLMs.

Efficient and practical quantum compiler towards multi-qubit systems with deep reinforcement learning

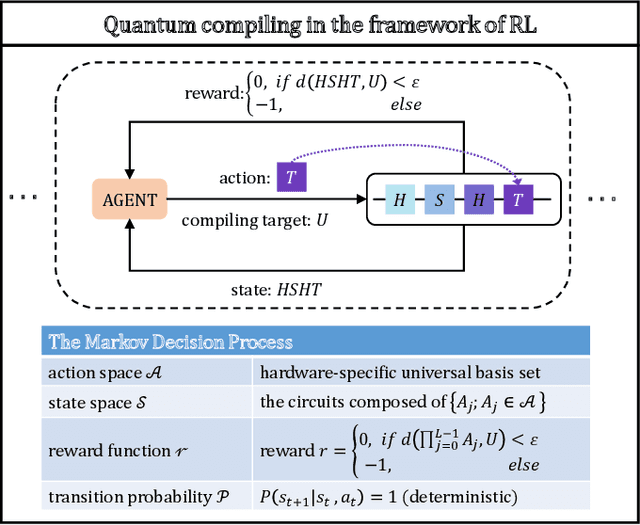
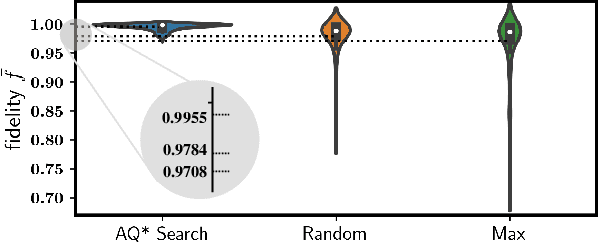
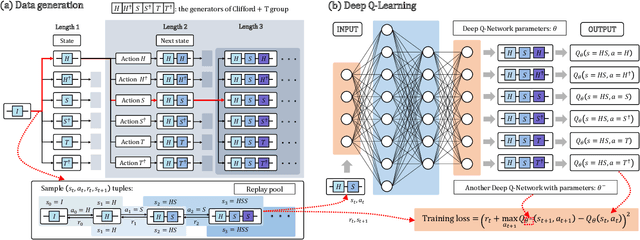
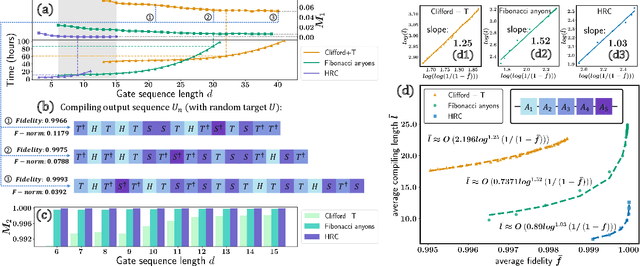
Efficient quantum compiling tactics greatly enhance the capability of quantum computers to execute complicated quantum algorithms. Due to its fundamental importance, a plethora of quantum compilers has been designed in past years. However, there are several caveats to current protocols, which are low optimality, high inference time, limited scalability, and lack of universality. To compensate for these defects, here we devise an efficient and practical quantum compiler assisted by advanced deep reinforcement learning (RL) techniques, i.e., data generation, deep Q-learning, and AQ* search. In this way, our protocol is compatible with various quantum machines and can be used to compile multi-qubit operators. We systematically evaluate the performance of our proposal in compiling quantum operators with both inverse-closed and inverse-free universal basis sets. In the task of single-qubit operator compiling, our proposal outperforms other RL-based quantum compilers in the measure of compiling sequence length and inference time. Meanwhile, the output solution is near-optimal, guaranteed by the Solovay-Kitaev theorem. Notably, for the inverse-free universal basis set, the achieved sequence length complexity is comparable with the inverse-based setting and dramatically advances previous methods. These empirical results contribute to improving the inverse-free Solovay-Kitaev theorem. In addition, for the first time, we demonstrate how to leverage RL-based quantum compilers to accomplish two-qubit operator compiling. The achieved results open an avenue for integrating RL with quantum compiling to unify efficiency and practicality and thus facilitate the exploration of quantum advantages.

The dilemma of quantum neural networks

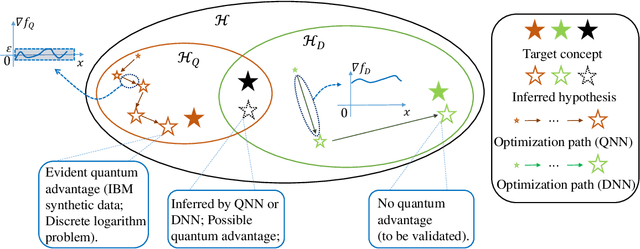
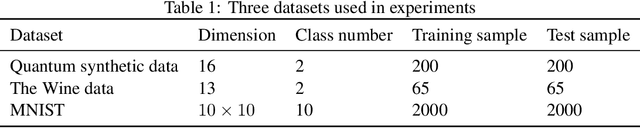
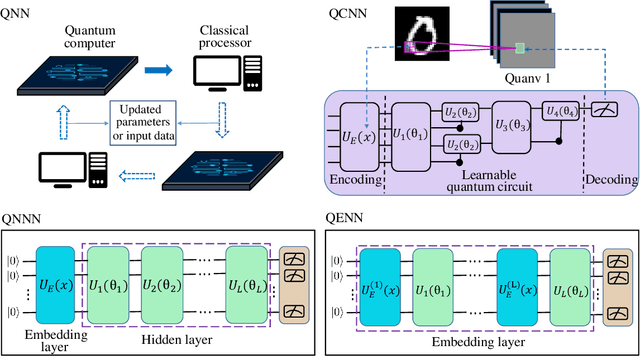
The core of quantum machine learning is to devise quantum models with good trainability and low generalization error bound than their classical counterparts to ensure better reliability and interpretability. Recent studies confirmed that quantum neural networks (QNNs) have the ability to achieve this goal on specific datasets. With this regard, it is of great importance to understand whether these advantages are still preserved on real-world tasks. Through systematic numerical experiments, we empirically observe that current QNNs fail to provide any benefit over classical learning models. Concretely, our results deliver two key messages. First, QNNs suffer from the severely limited effective model capacity, which incurs poor generalization on real-world datasets. Second, the trainability of QNNs is insensitive to regularization techniques, which sharply contrasts with the classical scenario. These empirical results force us to rethink the role of current QNNs and to design novel protocols for solving real-world problems with quantum advantages.

Exponential improvements for quantum-accessible reinforcement learning

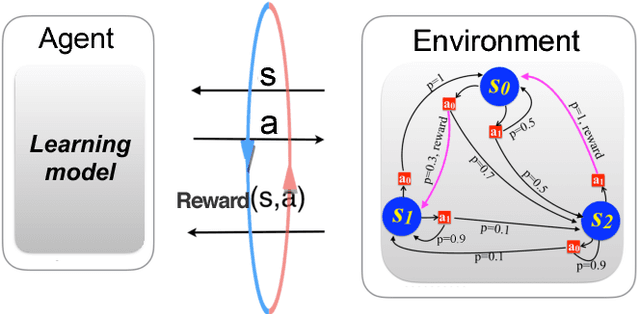
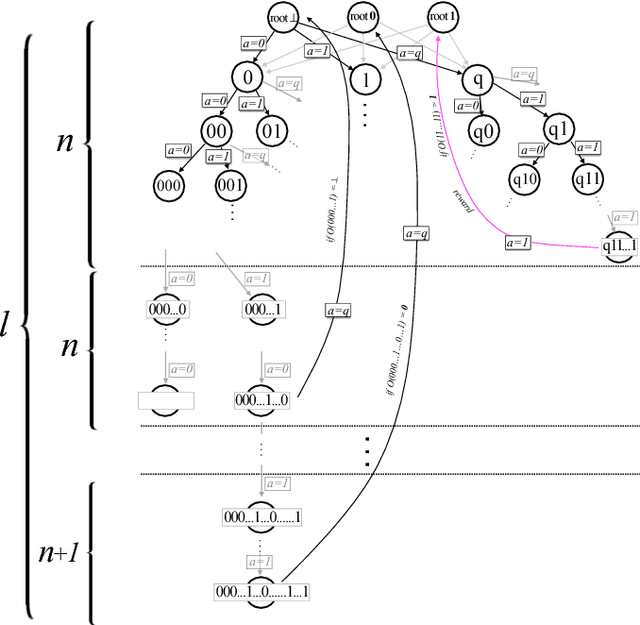
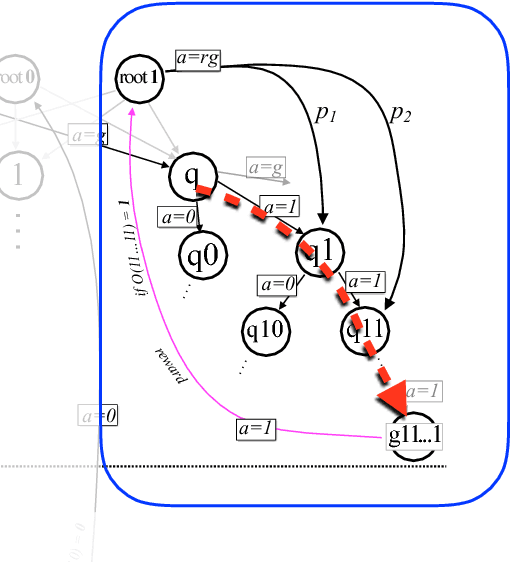
Quantum computers can offer dramatic improvements over classical devices for data analysis tasks such as prediction and classification. However, less is known about the advantages that quantum computers may bring in the setting of reinforcement learning, where learning is achieved via interaction with a task environment. Here, we consider a special case of reinforcement learning, where the task environment allows quantum access. In addition, we impose certain "naturalness" conditions on the task environment, which rule out the kinds of oracle problems that are studied in quantum query complexity (and for which quantum speedups are well-known). Within this framework of quantum-accessible reinforcement learning environments, we demonstrate that quantum agents can achieve exponential improvements in learning efficiency, surpassing previous results that showed only quadratic improvements. A key step in the proof is to construct task environments that encode well-known oracle problems, such as Simon's problem and Recursive Fourier Sampling, while satisfying the above "naturalness" conditions for reinforcement learning. Our results suggest that quantum agents may perform well in certain game-playing scenarios, where the game has recursive structure, and the agent can learn by playing against itself.