Jacob M. Taylor
Ax-Prover: A Deep Reasoning Agentic Framework for Theorem Proving in Mathematics and Quantum Physics
Oct 14, 2025Abstract:We present Ax-Prover, a multi-agent system for automated theorem proving in Lean that can solve problems across diverse scientific domains and operate either autonomously or collaboratively with human experts. To achieve this, Ax-Prover approaches scientific problem solving through formal proof generation, a process that demands both creative reasoning and strict syntactic rigor. Ax-Prover meets this challenge by equipping Large Language Models (LLMs), which provide knowledge and reasoning, with Lean tools via the Model Context Protocol (MCP), which ensure formal correctness. To evaluate its performance as an autonomous prover, we benchmark our approach against frontier LLMs and specialized prover models on two public math benchmarks and on two Lean benchmarks we introduce in the fields of abstract algebra and quantum theory. On public datasets, Ax-Prover is competitive with state-of-the-art provers, while it largely outperform them on the new benchmarks. This shows that, unlike specialized systems that struggle to generalize, our tool-based agentic theorem prover approach offers a generalizable methodology for formal verification across diverse scientific domains. Furthermore, we demonstrate Ax-Prover's assistant capabilities in a practical use case, showing how it enabled an expert mathematician to formalize the proof of a complex cryptography theorem.
Data Needs and Challenges of Quantum Dot Devices Automation: Workshop Report
Dec 21, 2023Abstract:Gate-defined quantum dots are a promising candidate system to realize scalable, coupled qubit systems and serve as a fundamental building block for quantum computers. However, present-day quantum dot devices suffer from imperfections that must be accounted for, which hinders the characterization, tuning, and operation process. Moreover, with an increasing number of quantum dot qubits, the relevant parameter space grows sufficiently to make heuristic control infeasible. Thus, it is imperative that reliable and scalable autonomous tuning approaches are developed. In this report, we outline current challenges in automating quantum dot device tuning and operation with a particular focus on datasets, benchmarking, and standardization. We also present ideas put forward by the quantum dot community on how to overcome them.
Colloquium: Advances in automation of quantum dot devices control
Dec 17, 2021



Abstract:Arrays of quantum dots (QDs) are a promising candidate system to realize scalable, coupled qubits systems and serve as a fundamental building block for quantum computers. In such semiconductor quantum systems, devices now have tens of individual electrostatic and dynamical voltages that must be carefully set to localize the system into the single-electron regime and to realize good qubit operational performance. The mapping of requisite dot locations and charges to gate voltages presents a challenging classical control problem. With an increasing number of QD qubits, the relevant parameter space grows sufficiently to make heuristic control unfeasible. In recent years, there has been a considerable effort to automate device control that combines script-based algorithms with machine learning (ML) techniques. In this Colloquium, we present a comprehensive overview of the recent progress in the automation of QD device control, with a particular emphasis on silicon- and GaAs-based QDs formed in two-dimensional electron gases. Combining physics-based modeling with modern numerical optimization and ML has proven quite effective in yielding efficient, scalable control. Further integration of theoretical, computational, and experimental efforts with computer science and ML holds tremendous potential in advancing semiconductor and other platforms for quantum computing.
Toward Robust Autotuning of Noisy Quantum Dot Devices
Jul 30, 2021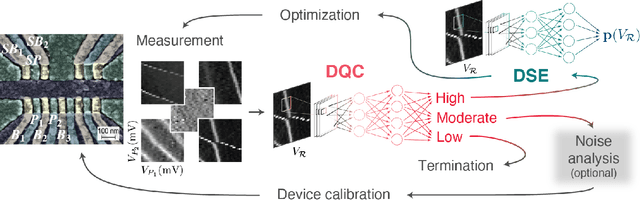
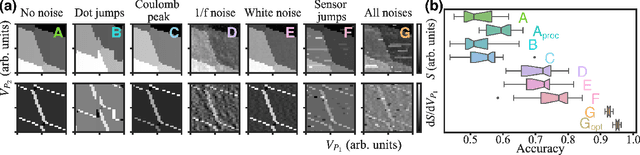
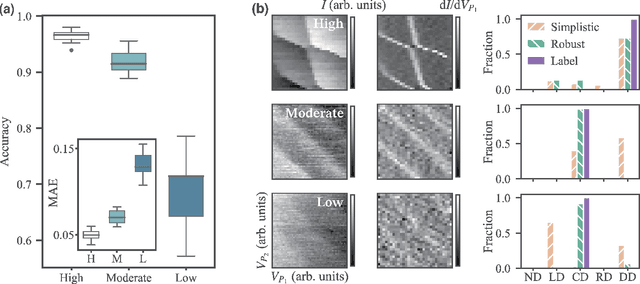
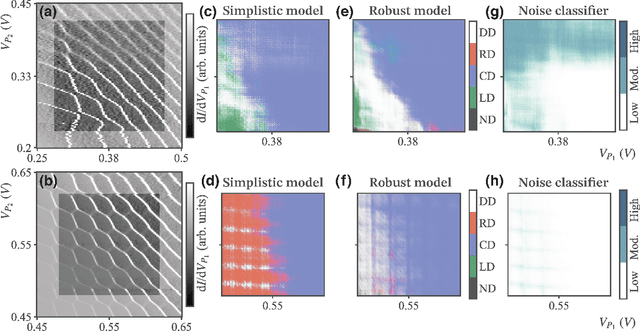
Abstract:The current autotuning approaches for quantum dot (QD) devices, while showing some success, lack an assessment of data reliability. This leads to unexpected failures when noisy data is processed by an autonomous system. In this work, we propose a framework for robust autotuning of QD devices that combines a machine learning (ML) state classifier with a data quality control module. The data quality control module acts as a ``gatekeeper'' system, ensuring that only reliable data is processed by the state classifier. Lower data quality results in either device recalibration or termination. To train both ML systems, we enhance the QD simulation by incorporating synthetic noise typical of QD experiments. We confirm that the inclusion of synthetic noise in the training of the state classifier significantly improves the performance, resulting in an accuracy of 95.1(7) % when tested on experimental data. We then validate the functionality of the data quality control module by showing the state classifier performance deteriorates with decreasing data quality, as expected. Our results establish a robust and flexible ML framework for autonomous tuning of noisy QD devices.
Theoretical bounds on data requirements for the ray-based classification
Mar 17, 2021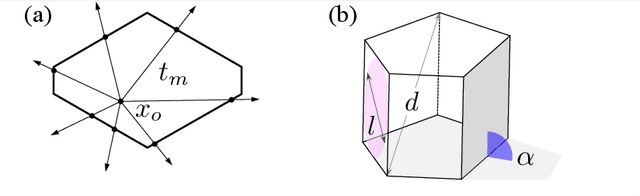
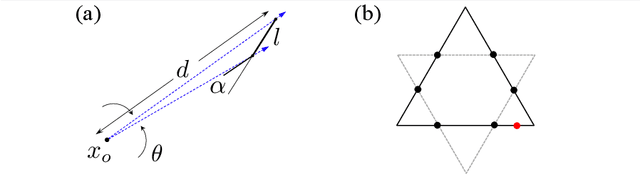
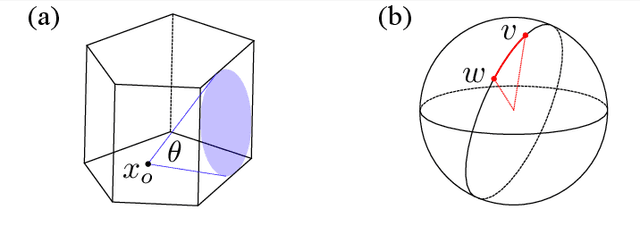
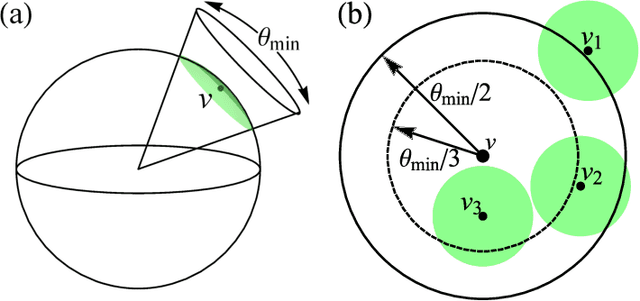
Abstract:The problem of classifying high-dimensional shapes in real-world data grows in complexity as the dimension of the space increases. For the case of identifying convex shapes of different geometries, a new classification framework has recently been proposed in which the intersections of a set of one-dimensional representations, called rays, with the boundaries of the shape are used to identify the specific geometry. This ray-based classification (RBC) has been empirically verified using a synthetic dataset of two- and three-dimensional shapes [1] and, more recently, has also been validated experimentally [2]. Here, we establish a bound on the number of rays necessary for shape classification, defined by key angular metrics, for arbitrary convex shapes. For two dimensions, we derive a lower bound on the number of rays in terms of the shape's length, diameter, and exterior angles. For convex polytopes in R^N, we generalize this result to a similar bound given as a function of the dihedral angle and the geometrical parameters of polygonal faces. This result enables a different approach for estimating high-dimensional shapes using substantially fewer data elements than volumetric or surface-based approaches.
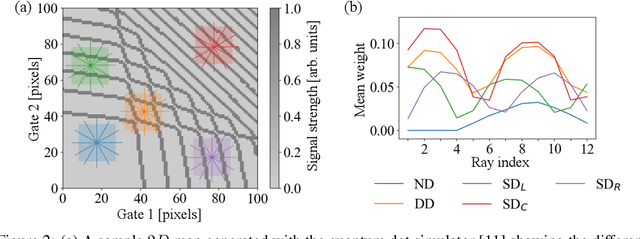
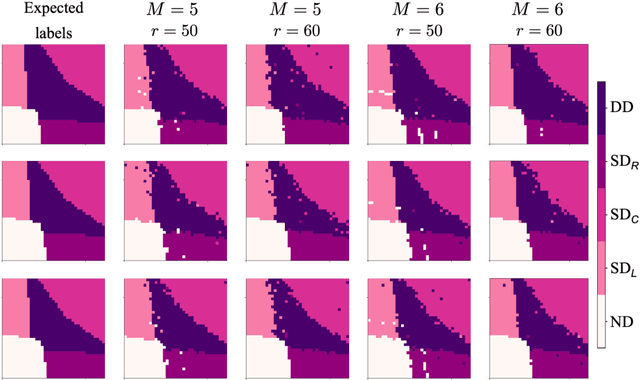
Ray-based framework for state identification in quantum dot devices
Feb 23, 2021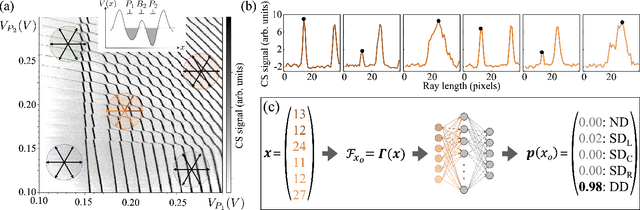
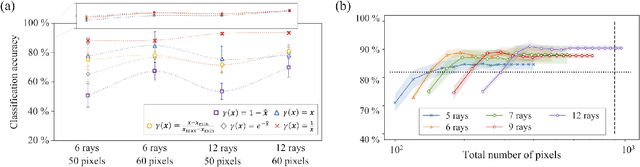
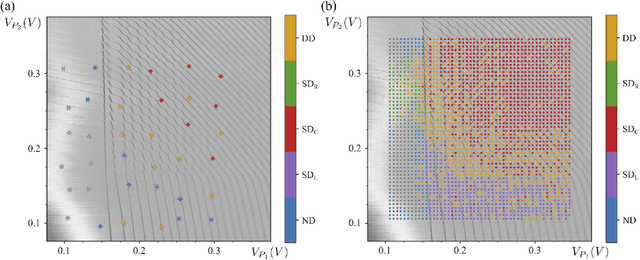
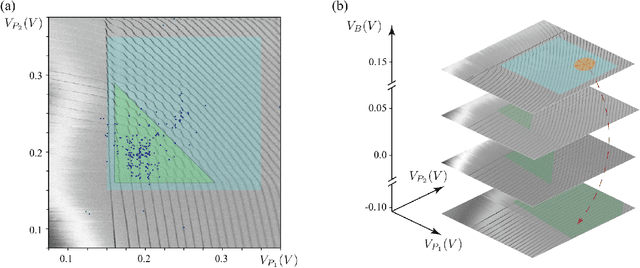
Abstract:Quantum dots (QDs) defined with electrostatic gates are a leading platform for a scalable quantum computing implementation. However, with increasing numbers of qubits, the complexity of the control parameter space also grows. Traditional measurement techniques, relying on complete or near-complete exploration via two-parameter scans (images) of the device response, quickly become impractical with increasing numbers of gates. Here, we propose to circumvent this challenge by introducing a measurement technique relying on one-dimensional projections of the device response in the multi-dimensional parameter space. Dubbed as the ray-based classification (RBC) framework, we use this machine learning (ML) approach to implement a classifier for QD states, enabling automated recognition of qubit-relevant parameter regimes. We show that RBC surpasses the 82 % accuracy benchmark from the experimental implementation of image-based classification techniques from prior work while cutting down the number of measurement points needed by up to 70 %. The reduction in measurement cost is a significant gain for time-intensive QD measurements and is a step forward towards the scalability of these devices. We also discuss how the RBC-based optimizer, which tunes the device to a multi-qubit regime, performs when tuning in the two- and three-dimensional parameter spaces defined by plunger and barrier gates that control the dots. This work provides experimental validation of both efficient state identification and optimization with ML techniques for non-traditional measurements in quantum systems with high-dimensional parameter spaces and time-intensive measurements.
Ray-based classification framework for high-dimensional data
Oct 01, 2020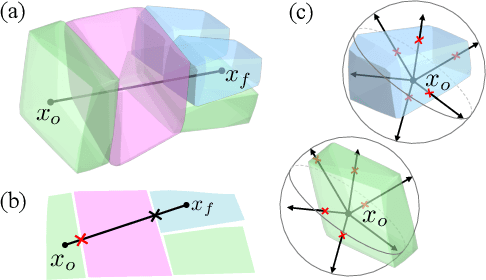
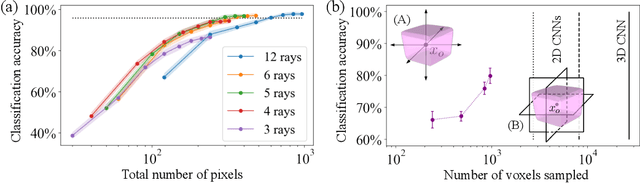
Abstract:While classification of arbitrary structures in high dimensions may require complete quantitative information, for simple geometrical structures, low-dimensional qualitative information about the boundaries defining the structures can suffice. Rather than using dense, multi-dimensional data, we propose a deep neural network (DNN) classification framework that utilizes a minimal collection of one-dimensional representations, called \emph{rays}, to construct the "fingerprint" of the structure(s) based on substantially reduced information. We empirically study this framework using a synthetic dataset of double and triple quantum dot devices and apply it to the classification problem of identifying the device state. We show that the performance of the ray-based classifier is already on par with traditional 2D images for low dimensional systems, while significantly cutting down the data acquisition cost.
Exponential improvements for quantum-accessible reinforcement learning
Aug 08, 2018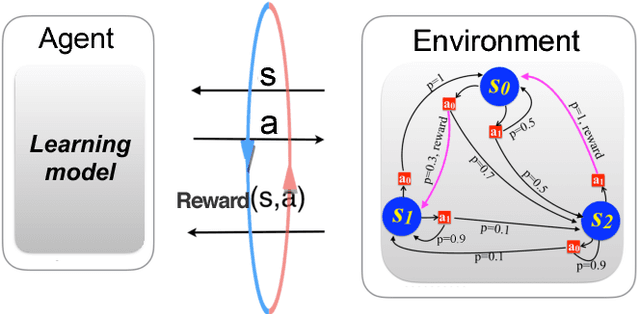

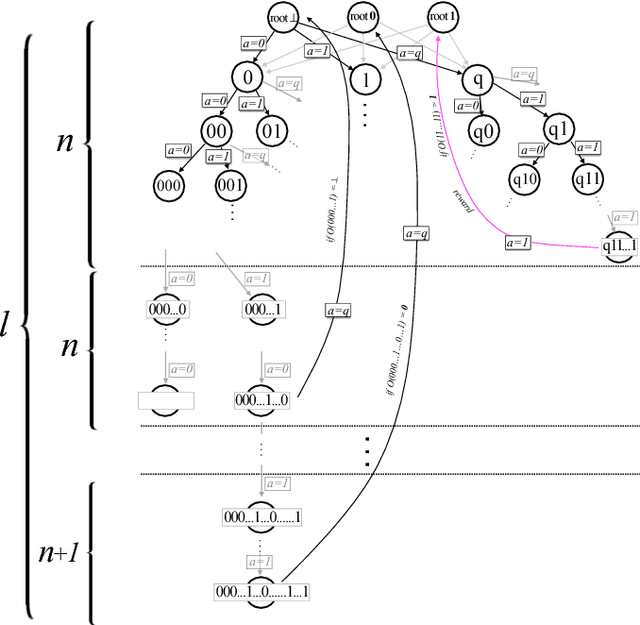
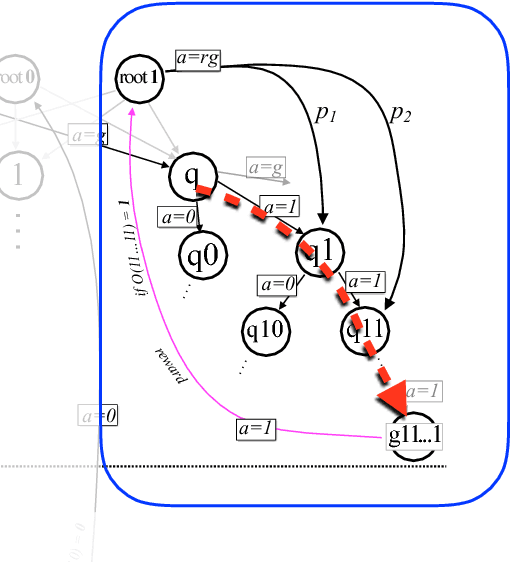
Abstract:Quantum computers can offer dramatic improvements over classical devices for data analysis tasks such as prediction and classification. However, less is known about the advantages that quantum computers may bring in the setting of reinforcement learning, where learning is achieved via interaction with a task environment. Here, we consider a special case of reinforcement learning, where the task environment allows quantum access. In addition, we impose certain "naturalness" conditions on the task environment, which rule out the kinds of oracle problems that are studied in quantum query complexity (and for which quantum speedups are well-known). Within this framework of quantum-accessible reinforcement learning environments, we demonstrate that quantum agents can achieve exponential improvements in learning efficiency, surpassing previous results that showed only quadratic improvements. A key step in the proof is to construct task environments that encode well-known oracle problems, such as Simon's problem and Recursive Fourier Sampling, while satisfying the above "naturalness" conditions for reinforcement learning. Our results suggest that quantum agents may perform well in certain game-playing scenarios, where the game has recursive structure, and the agent can learn by playing against itself.
Quantum-enhanced machine learning
Oct 26, 2016



Abstract:The emerging field of quantum machine learning has the potential to substantially aid in the problems and scope of artificial intelligence. This is only enhanced by recent successes in the field of classical machine learning. In this work we propose an approach for the systematic treatment of machine learning, from the perspective of quantum information. Our approach is general and covers all three main branches of machine learning: supervised, unsupervised and reinforcement learning. While quantum improvements in supervised and unsupervised learning have been reported, reinforcement learning has received much less attention. Within our approach, we tackle the problem of quantum enhancements in reinforcement learning as well, and propose a systematic scheme for providing improvements. As an example, we show that quadratic improvements in learning efficiency, and exponential improvements in performance over limited time periods, can be obtained for a broad class of learning problems.
* 5+15 pages. This paper builds upon and mostly supersedes arXiv:1507.08482. In addition to results provided in this previous work, here we achieve learning improvements in more general environments, and provide connections to other work in quantum machine learning. Explicit constructions of oracularized environments given in arXiv:1507.08482 are omitted in this version
Framework for learning agents in quantum environments
Jul 30, 2015



Abstract:In this paper we provide a broad framework for describing learning agents in general quantum environments. We analyze the types of classically specified environments which allow for quantum enhancements in learning, by contrasting environments to quantum oracles. We show that whether or not quantum improvements are at all possible depends on the internal structure of the quantum environment. If the environments are constructed and the internal structure is appropriately chosen, or if the agent has limited capacities to influence the internal states of the environment, we show that improvements in learning times are possible in a broad range of scenarios. Such scenarios we call luck-favoring settings. The case of constructed environments is particularly relevant for the class of model-based learning agents, where our results imply a near-generic improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge