Classifying single-qubit noise using machine learning

Quantum characterization, validation, and verification (QCVV) techniques are used to probe, characterize, diagnose, and detect errors in quantum information processors (QIPs). An important component of any QCVV protocol is a mapping from experimental data to an estimate of a property of a QIP. Machine learning (ML) algorithms can help automate the development of QCVV protocols, creating such maps by learning them from training data. We identify the critical components of "machine-learned" QCVV techniques, and present a rubric for developing them. To demonstrate this approach, we focus on the problem of determining whether noise affecting a single qubit is coherent or stochastic (incoherent) using the data sets originally proposed for gate set tomography. We leverage known ML algorithms to train a classifier distinguishing these two kinds of noise. The accuracy of the classifier depends on how well it can approximate the "natural" geometry of the training data. We find GST data sets generated by a noisy qubit can reliably be separated by linear surfaces, although feature engineering can be necessary. We also show the classifier learned by a support vector machine (SVM) is robust under finite-sample noise.

Exponential improvements for quantum-accessible reinforcement learning

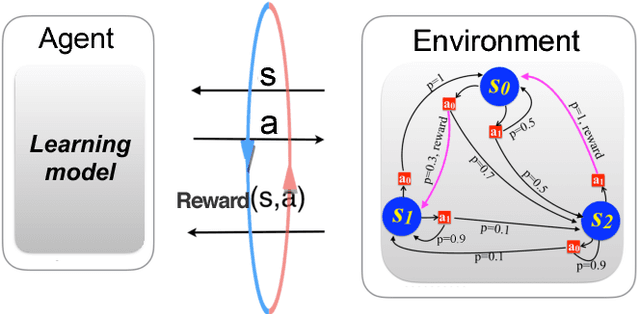
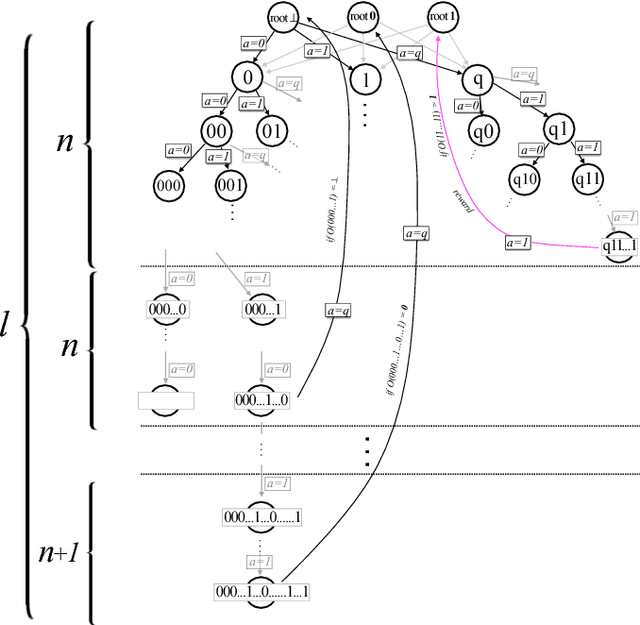
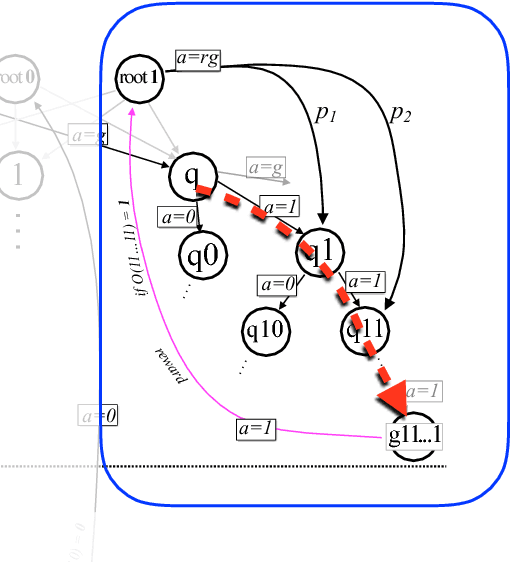
Quantum computers can offer dramatic improvements over classical devices for data analysis tasks such as prediction and classification. However, less is known about the advantages that quantum computers may bring in the setting of reinforcement learning, where learning is achieved via interaction with a task environment. Here, we consider a special case of reinforcement learning, where the task environment allows quantum access. In addition, we impose certain "naturalness" conditions on the task environment, which rule out the kinds of oracle problems that are studied in quantum query complexity (and for which quantum speedups are well-known). Within this framework of quantum-accessible reinforcement learning environments, we demonstrate that quantum agents can achieve exponential improvements in learning efficiency, surpassing previous results that showed only quadratic improvements. A key step in the proof is to construct task environments that encode well-known oracle problems, such as Simon's problem and Recursive Fourier Sampling, while satisfying the above "naturalness" conditions for reinforcement learning. Our results suggest that quantum agents may perform well in certain game-playing scenarios, where the game has recursive structure, and the agent can learn by playing against itself.

A Spectral Algorithm for Latent Dirichlet Allocation

The problem of topic modeling can be seen as a generalization of the clustering problem, in that it posits that observations are generated due to multiple latent factors (e.g., the words in each document are generated as a mixture of several active topics, as opposed to just one). This increased representational power comes at the cost of a more challenging unsupervised learning problem of estimating the topic probability vectors (the distributions over words for each topic), when only the words are observed and the corresponding topics are hidden. We provide a simple and efficient learning procedure that is guaranteed to recover the parameters for a wide class of mixture models, including the popular latent Dirichlet allocation (LDA) model. For LDA, the procedure correctly recovers both the topic probability vectors and the prior over the topics, using only trigram statistics (i.e., third order moments, which may be estimated with documents containing just three words). The method, termed Excess Correlation Analysis (ECA), is based on a spectral decomposition of low order moments (third and fourth order) via two singular value decompositions (SVDs). Moreover, the algorithm is scalable since the SVD operations are carried out on $k\times k$ matrices, where $k$ is the number of latent factors (e.g. the number of topics), rather than in the $d$-dimensional observed space (typically $d \gg k$).

Universal low-rank matrix recovery from Pauli measurements

We study the problem of reconstructing an unknown matrix M of rank r and dimension d using O(rd poly log d) Pauli measurements. This has applications in quantum state tomography, and is a non-commutative analogue of a well-known problem in compressed sensing: recovering a sparse vector from a few of its Fourier coefficients. We show that almost all sets of O(rd log^6 d) Pauli measurements satisfy the rank-r restricted isometry property (RIP). This implies that M can be recovered from a fixed ("universal") set of Pauli measurements, using nuclear-norm minimization (e.g., the matrix Lasso), with nearly-optimal bounds on the error. A similar result holds for any class of measurements that use an orthonormal operator basis whose elements have small operator norm. Our proof uses Dudley's inequality for Gaussian processes, together with bounds on covering numbers obtained via entropy duality.