Sandesh S. Kalantre
Toward Robust Autotuning of Noisy Quantum Dot Devices
Jul 30, 2021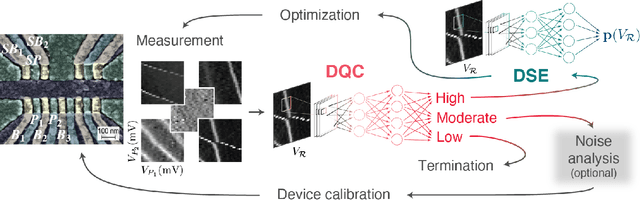
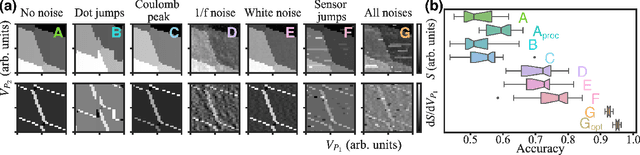
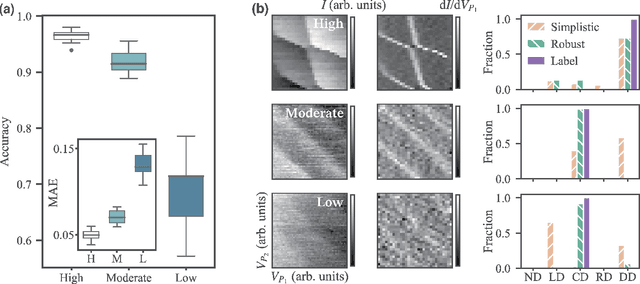
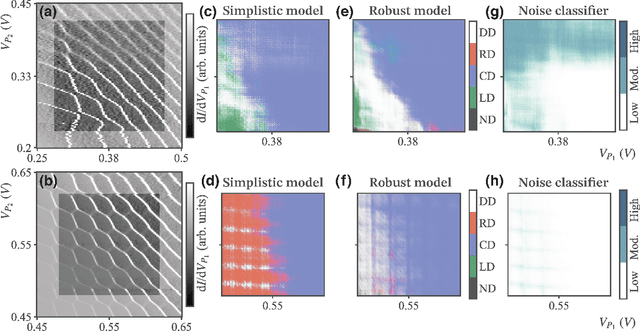
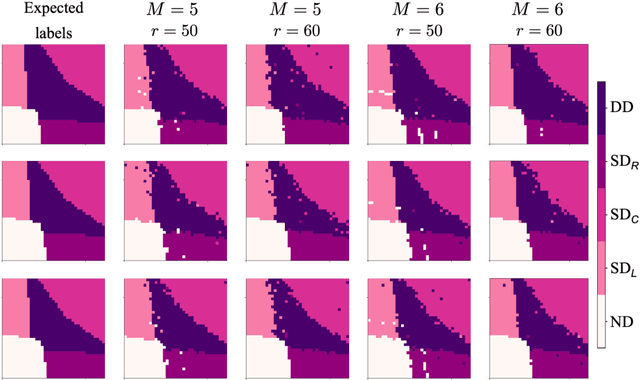
Abstract:The current autotuning approaches for quantum dot (QD) devices, while showing some success, lack an assessment of data reliability. This leads to unexpected failures when noisy data is processed by an autonomous system. In this work, we propose a framework for robust autotuning of QD devices that combines a machine learning (ML) state classifier with a data quality control module. The data quality control module acts as a ``gatekeeper'' system, ensuring that only reliable data is processed by the state classifier. Lower data quality results in either device recalibration or termination. To train both ML systems, we enhance the QD simulation by incorporating synthetic noise typical of QD experiments. We confirm that the inclusion of synthetic noise in the training of the state classifier significantly improves the performance, resulting in an accuracy of 95.1(7) % when tested on experimental data. We then validate the functionality of the data quality control module by showing the state classifier performance deteriorates with decreasing data quality, as expected. Our results establish a robust and flexible ML framework for autonomous tuning of noisy QD devices.
Theoretical bounds on data requirements for the ray-based classification
Mar 17, 2021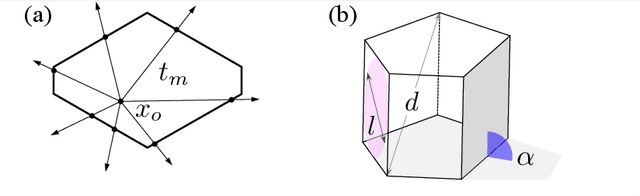
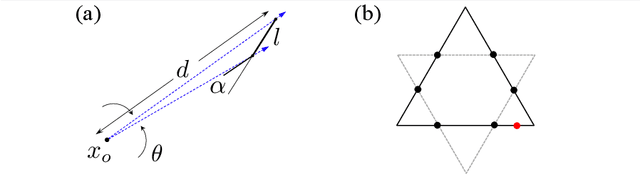
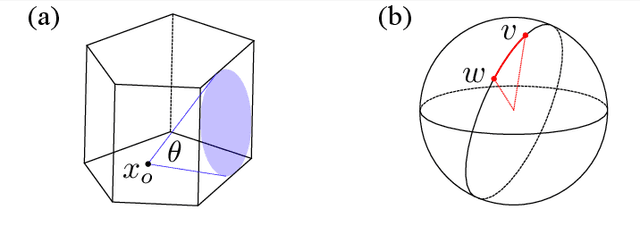
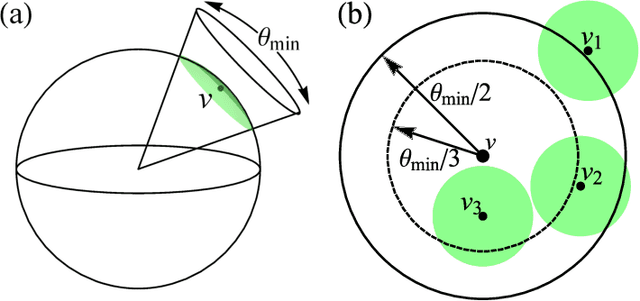
Abstract:The problem of classifying high-dimensional shapes in real-world data grows in complexity as the dimension of the space increases. For the case of identifying convex shapes of different geometries, a new classification framework has recently been proposed in which the intersections of a set of one-dimensional representations, called rays, with the boundaries of the shape are used to identify the specific geometry. This ray-based classification (RBC) has been empirically verified using a synthetic dataset of two- and three-dimensional shapes [1] and, more recently, has also been validated experimentally [2]. Here, we establish a bound on the number of rays necessary for shape classification, defined by key angular metrics, for arbitrary convex shapes. For two dimensions, we derive a lower bound on the number of rays in terms of the shape's length, diameter, and exterior angles. For convex polytopes in R^N, we generalize this result to a similar bound given as a function of the dihedral angle and the geometrical parameters of polygonal faces. This result enables a different approach for estimating high-dimensional shapes using substantially fewer data elements than volumetric or surface-based approaches.
Ray-based framework for state identification in quantum dot devices
Feb 23, 2021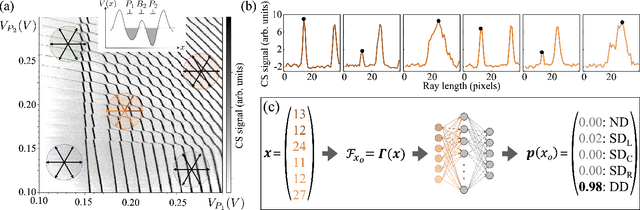
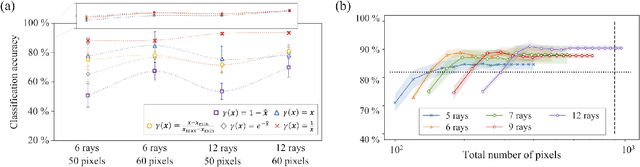
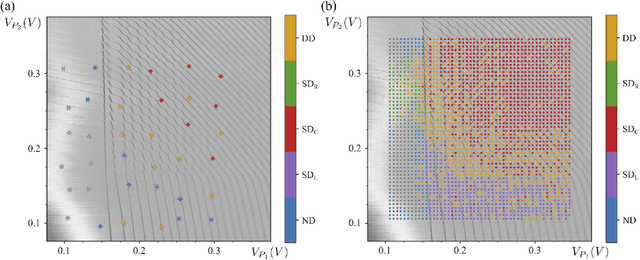
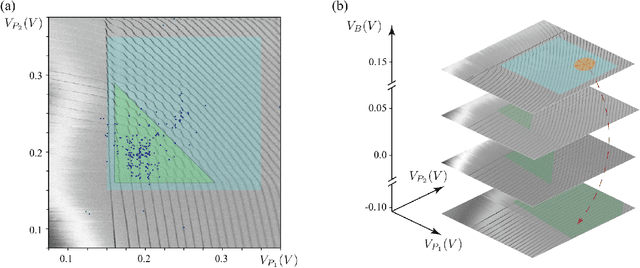
Abstract:Quantum dots (QDs) defined with electrostatic gates are a leading platform for a scalable quantum computing implementation. However, with increasing numbers of qubits, the complexity of the control parameter space also grows. Traditional measurement techniques, relying on complete or near-complete exploration via two-parameter scans (images) of the device response, quickly become impractical with increasing numbers of gates. Here, we propose to circumvent this challenge by introducing a measurement technique relying on one-dimensional projections of the device response in the multi-dimensional parameter space. Dubbed as the ray-based classification (RBC) framework, we use this machine learning (ML) approach to implement a classifier for QD states, enabling automated recognition of qubit-relevant parameter regimes. We show that RBC surpasses the 82 % accuracy benchmark from the experimental implementation of image-based classification techniques from prior work while cutting down the number of measurement points needed by up to 70 %. The reduction in measurement cost is a significant gain for time-intensive QD measurements and is a step forward towards the scalability of these devices. We also discuss how the RBC-based optimizer, which tunes the device to a multi-qubit regime, performs when tuning in the two- and three-dimensional parameter spaces defined by plunger and barrier gates that control the dots. This work provides experimental validation of both efficient state identification and optimization with ML techniques for non-traditional measurements in quantum systems with high-dimensional parameter spaces and time-intensive measurements.
Ray-based classification framework for high-dimensional data
Oct 01, 2020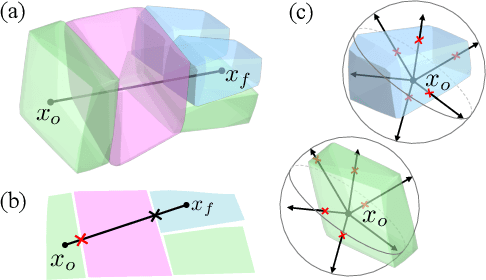
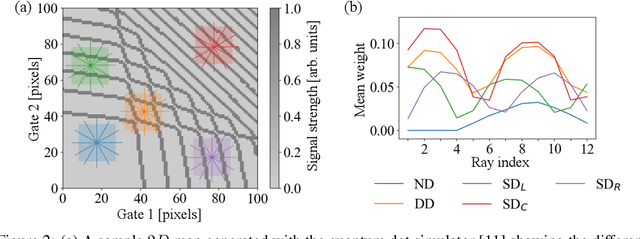
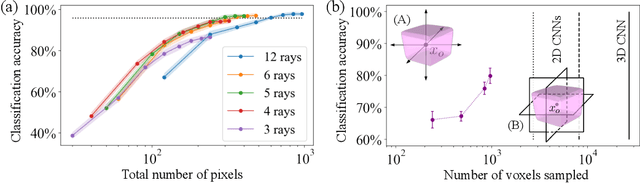
Abstract:While classification of arbitrary structures in high dimensions may require complete quantitative information, for simple geometrical structures, low-dimensional qualitative information about the boundaries defining the structures can suffice. Rather than using dense, multi-dimensional data, we propose a deep neural network (DNN) classification framework that utilizes a minimal collection of one-dimensional representations, called \emph{rays}, to construct the "fingerprint" of the structure(s) based on substantially reduced information. We empirically study this framework using a synthetic dataset of double and triple quantum dot devices and apply it to the classification problem of identifying the device state. We show that the performance of the ray-based classifier is already on par with traditional 2D images for low dimensional systems, while significantly cutting down the data acquisition cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge