Theoretical bounds on data requirements for the ray-based classification
Paper and Code
Mar 17, 2021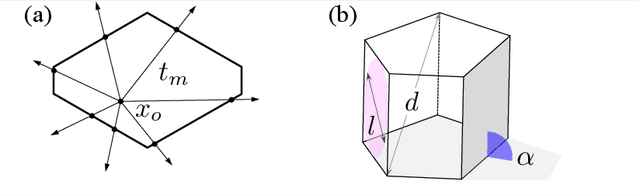
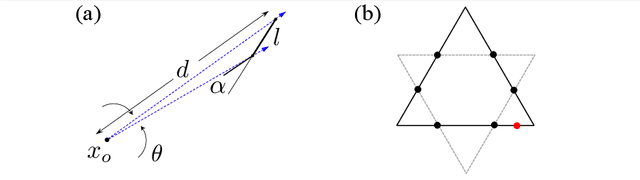
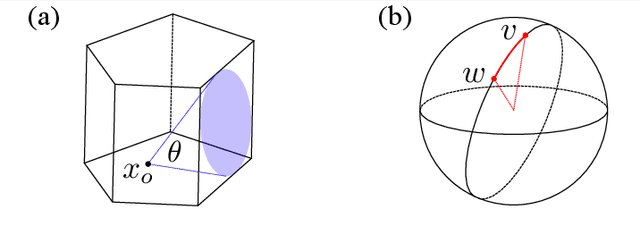
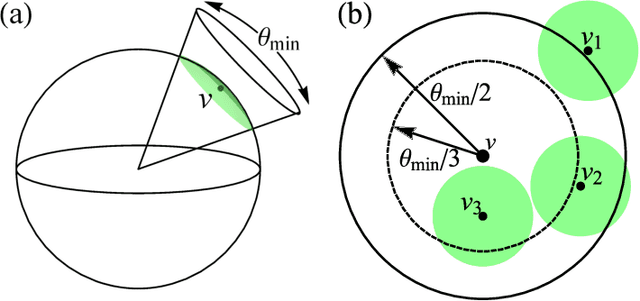
The problem of classifying high-dimensional shapes in real-world data grows in complexity as the dimension of the space increases. For the case of identifying convex shapes of different geometries, a new classification framework has recently been proposed in which the intersections of a set of one-dimensional representations, called rays, with the boundaries of the shape are used to identify the specific geometry. This ray-based classification (RBC) has been empirically verified using a synthetic dataset of two- and three-dimensional shapes [1] and, more recently, has also been validated experimentally [2]. Here, we establish a bound on the number of rays necessary for shape classification, defined by key angular metrics, for arbitrary convex shapes. For two dimensions, we derive a lower bound on the number of rays in terms of the shape's length, diameter, and exterior angles. For convex polytopes in R^N, we generalize this result to a similar bound given as a function of the dihedral angle and the geometrical parameters of polygonal faces. This result enables a different approach for estimating high-dimensional shapes using substantially fewer data elements than volumetric or surface-based approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge