Kaining Zhang
TITAN: A Trajectory-Informed Technique for Adaptive Parameter Freezing in Large-Scale VQE
Sep 18, 2025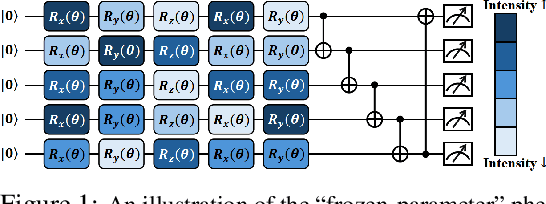
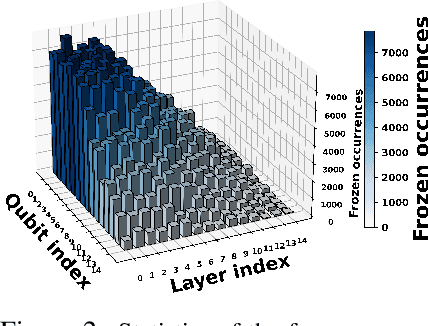
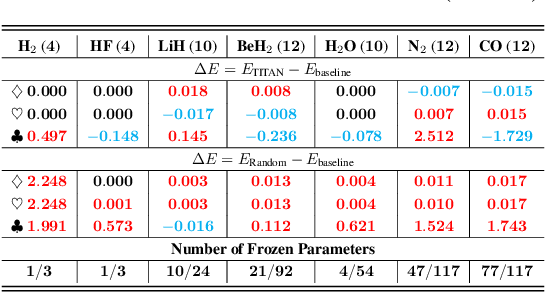
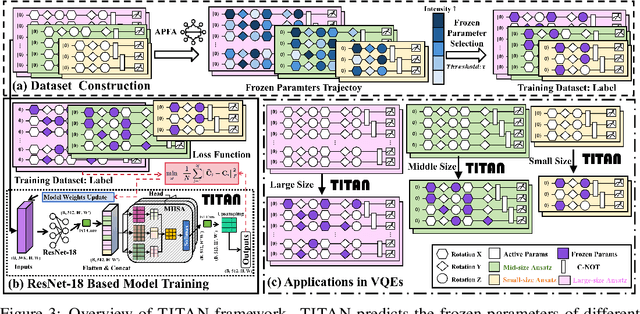
Abstract:Variational quantum Eigensolver (VQE) is a leading candidate for harnessing quantum computers to advance quantum chemistry and materials simulations, yet its training efficiency deteriorates rapidly for large Hamiltonians. Two issues underlie this bottleneck: (i) the no-cloning theorem imposes a linear growth in circuit evaluations with the number of parameters per gradient step; and (ii) deeper circuits encounter barren plateaus (BPs), leading to exponentially increasing measurement overheads. To address these challenges, here we propose a deep learning framework, dubbed Titan, which identifies and freezes inactive parameters of a given ansatze at initialization for a specific class of Hamiltonians, reducing the optimization overhead without sacrificing accuracy. The motivation of Titan starts with our empirical findings that a subset of parameters consistently has a negligible influence on training dynamics. Its design combines a theoretically grounded data construction strategy, ensuring each training example is informative and BP-resilient, with an adaptive neural architecture that generalizes across ansatze of varying sizes. Across benchmark transverse-field Ising models, Heisenberg models, and multiple molecule systems up to 30 qubits, Titan achieves up to 3 times faster convergence and 40% to 60% fewer circuit evaluations than state-of-the-art baselines, while matching or surpassing their estimation accuracy. By proactively trimming parameter space, Titan lowers hardware demands and offers a scalable path toward utilizing VQE to advance practical quantum chemistry and materials science.
Deep Learning Reforms Image Matching: A Survey and Outlook
Jun 05, 2025Abstract:Image matching, which establishes correspondences between two-view images to recover 3D structure and camera geometry, serves as a cornerstone in computer vision and underpins a wide range of applications, including visual localization, 3D reconstruction, and simultaneous localization and mapping (SLAM). Traditional pipelines composed of ``detector-descriptor, feature matcher, outlier filter, and geometric estimator'' falter in challenging scenarios. Recent deep-learning advances have significantly boosted both robustness and accuracy. This survey adopts a unique perspective by comprehensively reviewing how deep learning has incrementally transformed the classical image matching pipeline. Our taxonomy highly aligns with the traditional pipeline in two key aspects: i) the replacement of individual steps in the traditional pipeline with learnable alternatives, including learnable detector-descriptor, outlier filter, and geometric estimator; and ii) the merging of multiple steps into end-to-end learnable modules, encompassing middle-end sparse matcher, end-to-end semi-dense/dense matcher, and pose regressor. We first examine the design principles, advantages, and limitations of both aspects, and then benchmark representative methods on relative pose recovery, homography estimation, and visual localization tasks. Finally, we discuss open challenges and outline promising directions for future research. By systematically categorizing and evaluating deep learning-driven strategies, this survey offers a clear overview of the evolving image matching landscape and highlights key avenues for further innovation.
Quantum Machine Learning: A Hands-on Tutorial for Machine Learning Practitioners and Researchers
Feb 03, 2025Abstract:This tutorial intends to introduce readers with a background in AI to quantum machine learning (QML) -- a rapidly evolving field that seeks to leverage the power of quantum computers to reshape the landscape of machine learning. For self-consistency, this tutorial covers foundational principles, representative QML algorithms, their potential applications, and critical aspects such as trainability, generalization, and computational complexity. In addition, practical code demonstrations are provided in https://qml-tutorial.github.io/ to illustrate real-world implementations and facilitate hands-on learning. Together, these elements offer readers a comprehensive overview of the latest advancements in QML. By bridging the gap between classical machine learning and quantum computing, this tutorial serves as a valuable resource for those looking to engage with QML and explore the forefront of AI in the quantum era.
The curse of random quantum data
Aug 19, 2024Abstract:Quantum machine learning, which involves running machine learning algorithms on quantum devices, may be one of the most significant flagship applications for these devices. Unlike its classical counterparts, the role of data in quantum machine learning has not been fully understood. In this work, we quantify the performances of quantum machine learning in the landscape of quantum data. Provided that the encoding of quantum data is sufficiently random, the performance, we find that the training efficiency and generalization capabilities in quantum machine learning will be exponentially suppressed with the increase in the number of qubits, which we call "the curse of random quantum data". Our findings apply to both the quantum kernel method and the large-width limit of quantum neural networks. Conversely, we highlight that through meticulous design of quantum datasets, it is possible to avoid these curses, thereby achieving efficient convergence and robust generalization. Our conclusions are corroborated by extensive numerical simulations.
Quantum Imitation Learning
Apr 04, 2023Abstract:Despite remarkable successes in solving various complex decision-making tasks, training an imitation learning (IL) algorithm with deep neural networks (DNNs) suffers from the high computation burden. In this work, we propose quantum imitation learning (QIL) with a hope to utilize quantum advantage to speed up IL. Concretely, we develop two QIL algorithms, quantum behavioural cloning (Q-BC) and quantum generative adversarial imitation learning (Q-GAIL). Q-BC is trained with a negative log-likelihood loss in an off-line manner that suits extensive expert data cases, whereas Q-GAIL works in an inverse reinforcement learning scheme, which is on-line and on-policy that is suitable for limited expert data cases. For both QIL algorithms, we adopt variational quantum circuits (VQCs) in place of DNNs for representing policies, which are modified with data re-uploading and scaling parameters to enhance the expressivity. We first encode classical data into quantum states as inputs, then perform VQCs, and finally measure quantum outputs to obtain control signals of agents. Experiment results demonstrate that both Q-BC and Q-GAIL can achieve comparable performance compared to classical counterparts, with the potential of quantum speed-up. To our knowledge, we are the first to propose the concept of QIL and conduct pilot studies, which paves the way for the quantum era.
A Comprehensive Review on Deep Supervision: Theories and Applications
Jul 06, 2022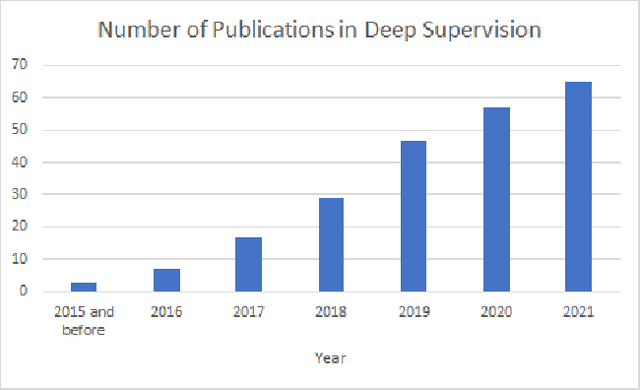
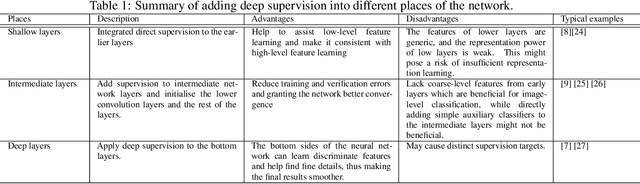
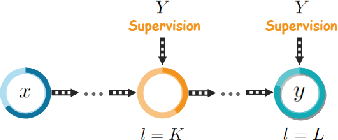

Abstract:Deep supervision, or known as 'intermediate supervision' or 'auxiliary supervision', is to add supervision at hidden layers of a neural network. This technique has been increasingly applied in deep neural network learning systems for various computer vision applications recently. There is a consensus that deep supervision helps improve neural network performance by alleviating the gradient vanishing problem, as one of the many strengths of deep supervision. Besides, in different computer vision applications, deep supervision can be applied in different ways. How to make the most use of deep supervision to improve network performance in different applications has not been thoroughly investigated. In this paper, we provide a comprehensive in-depth review of deep supervision in both theories and applications. We propose a new classification of different deep supervision networks, and discuss advantages and limitations of current deep supervision networks in computer vision applications.
Recent Advances for Quantum Neural Networks in Generative Learning
Jun 07, 2022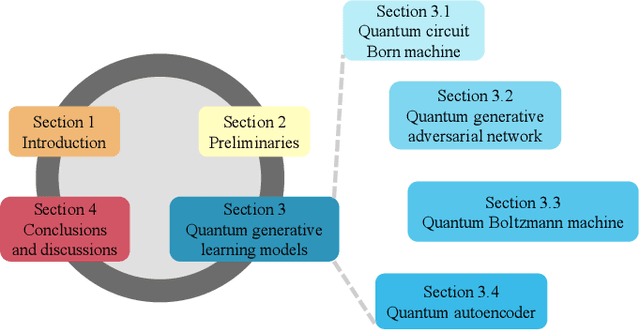

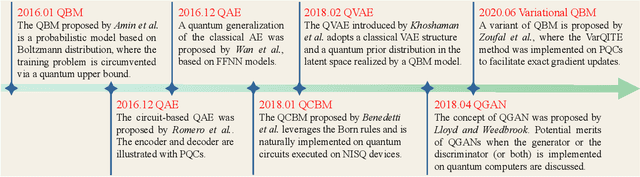
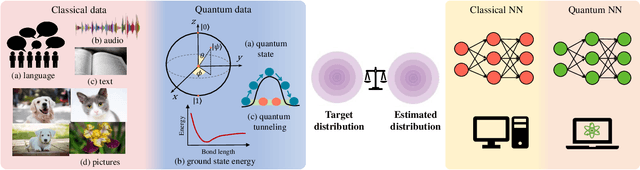
Abstract:Quantum computers are next-generation devices that hold promise to perform calculations beyond the reach of classical computers. A leading method towards achieving this goal is through quantum machine learning, especially quantum generative learning. Due to the intrinsic probabilistic nature of quantum mechanics, it is reasonable to postulate that quantum generative learning models (QGLMs) may surpass their classical counterparts. As such, QGLMs are receiving growing attention from the quantum physics and computer science communities, where various QGLMs that can be efficiently implemented on near-term quantum machines with potential computational advantages are proposed. In this paper, we review the current progress of QGLMs from the perspective of machine learning. Particularly, we interpret these QGLMs, covering quantum circuit born machines, quantum generative adversarial networks, quantum Boltzmann machines, and quantum autoencoders, as the quantum extension of classical generative learning models. In this context, we explore their intrinsic relation and their fundamental differences. We further summarize the potential applications of QGLMs in both conventional machine learning tasks and quantum physics. Last, we discuss the challenges and further research directions for QGLMs.
Gaussian initializations help deep variational quantum circuits escape from the barren plateau
Mar 17, 2022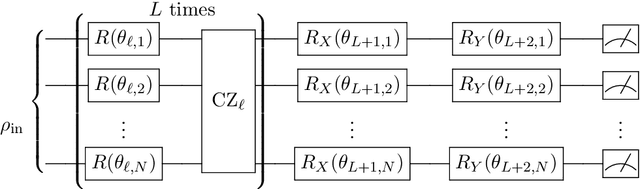
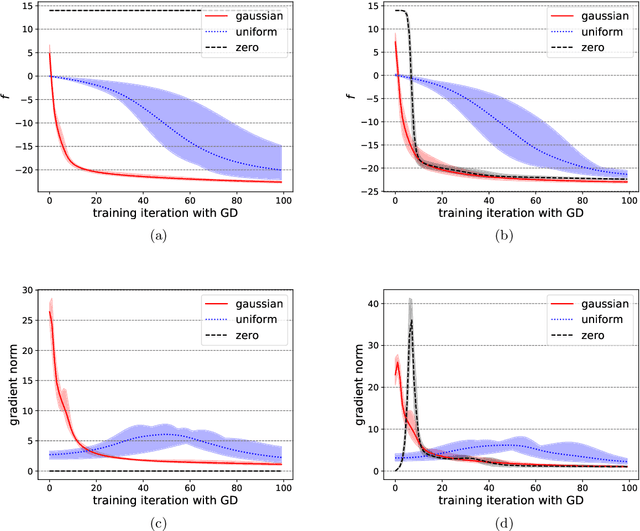
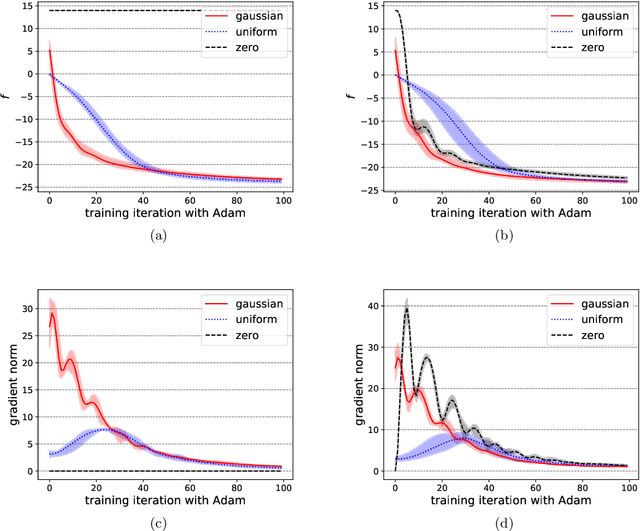
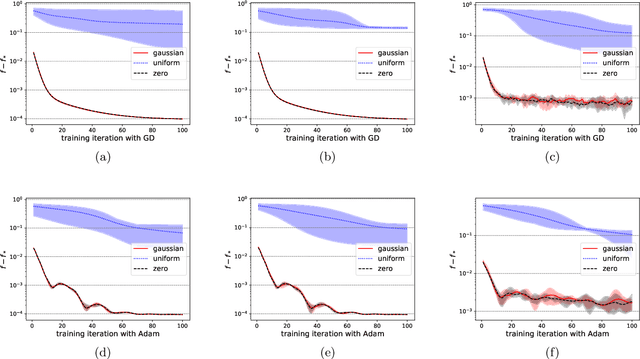
Abstract:Variational quantum circuits have been widely employed in quantum simulation and quantum machine learning in recent years. However, quantum circuits with random structures have poor trainability due to the exponentially vanishing gradient with respect to the circuit depth and the qubit number. This result leads to a general belief that deep quantum circuits will not be feasible for practical tasks. In this work, we propose an initialization strategy with theoretical guarantees for the vanishing gradient problem in general deep circuits. Specifically, we prove that under proper Gaussian initialized parameters, the norm of the gradient decays at most polynomially when the qubit number and the circuit depth increase. Our theoretical results hold for both the local and the global observable cases, where the latter was believed to have vanishing gradients even for shallow circuits. Experimental results verify our theoretical findings in the quantum simulation and quantum chemistry.
Quantum algorithm for finding the negative curvature direction in non-convex optimization
Sep 17, 2019

Abstract:We present an efficient quantum algorithm aiming to find the negative curvature direction for escaping the saddle point, which is the critical subroutine for many second-order non-convex optimization algorithms. We prove that our algorithm could produce the target state corresponding to the negative curvature direction with query complexity O(polylog(d) /{\epsilon}), where d is the dimension of the optimization function. The quantum negative curvature finding algorithm is exponentially faster than any known classical method which takes time at least O(d /\sqrt{\epsilon}). Moreover, we propose an efficient quantum algorithm to achieve the classical read-out of the target state. Our classical read-out algorithm runs exponentially faster on the degree of d than existing counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge