Gaussian initializations help deep variational quantum circuits escape from the barren plateau

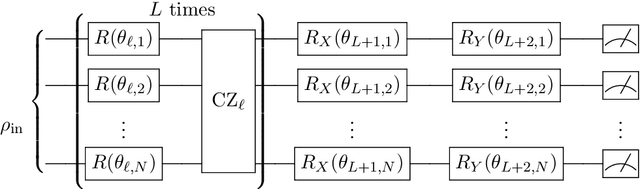
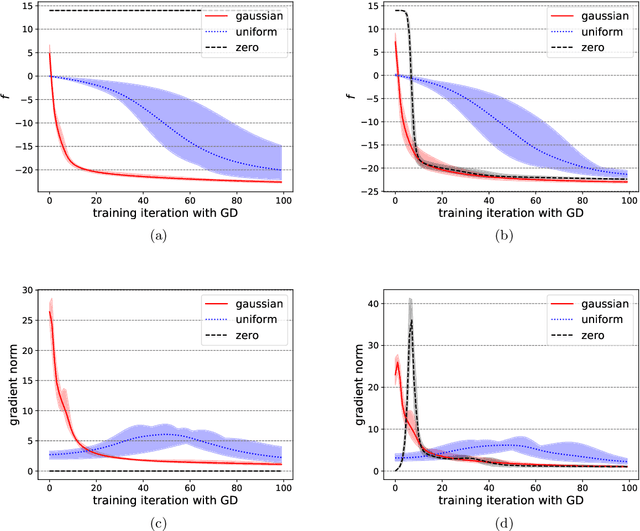
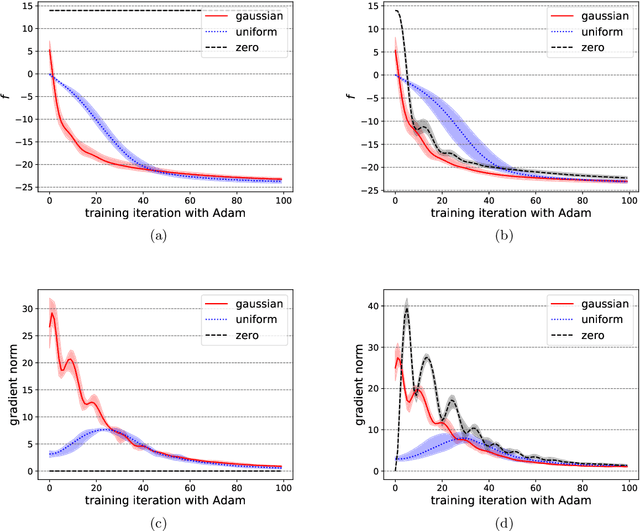
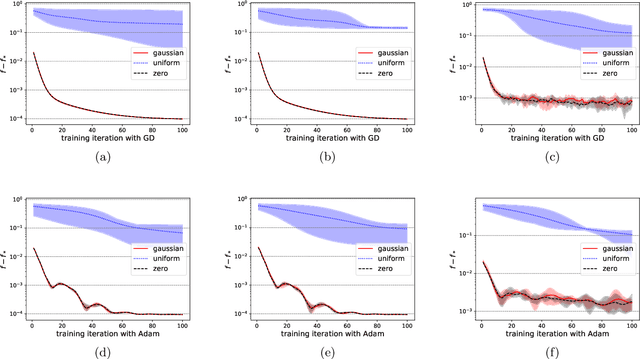
Variational quantum circuits have been widely employed in quantum simulation and quantum machine learning in recent years. However, quantum circuits with random structures have poor trainability due to the exponentially vanishing gradient with respect to the circuit depth and the qubit number. This result leads to a general belief that deep quantum circuits will not be feasible for practical tasks. In this work, we propose an initialization strategy with theoretical guarantees for the vanishing gradient problem in general deep circuits. Specifically, we prove that under proper Gaussian initialized parameters, the norm of the gradient decays at most polynomially when the qubit number and the circuit depth increase. Our theoretical results hold for both the local and the global observable cases, where the latter was believed to have vanishing gradients even for shallow circuits. Experimental results verify our theoretical findings in the quantum simulation and quantum chemistry.