Subspace-Based Detection in OFDM ISAC Systems under Different Constellations

This paper investigates subspace-based target detection in OFDM integrated sensing and communications (ISAC) systems, considering the impact of various constellations. To meet diverse communication demands, different constellation schemes with varying modulation orders (e.g., PSK, QAM) can be employed, which in turn leads to variations in peak sidelobe levels (PSLs) within the radar functionality. These PSL fluctuations pose a significant challenge in the context of multi-target detection, particularly in scenarios where strong sidelobe masking effects manifest. To tackle this challenge, we have devised a subspace-based approach for a step-by-step target detection process, systematically eliminating interference stemming from detected targets. Simulation results corroborate the effectiveness of the proposed method in achieving consistently high target detection performance under a wide range of constellation options in OFDM ISAC systems.

Team AcieLee: Technical Report for EPIC-SOUNDS Audio-Based Interaction Recognition Challenge 2023

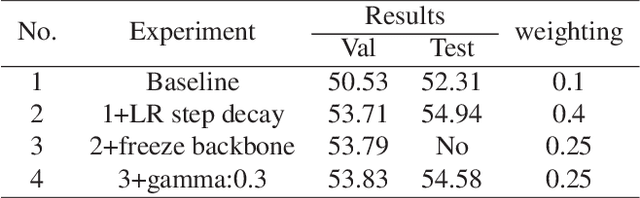
In this report, we describe the technical details of our submission to the EPIC-SOUNDS Audio-Based Interaction Recognition Challenge 2023, by Team "AcieLee" (username: Yuqi\_Li). The task is to classify the audio caused by interactions between objects, or from events of the camera wearer. We conducted exhaustive experiments and found learning rate step decay, backbone frozen, label smoothing and focal loss contribute most to the performance improvement. After training, we combined multiple models from different stages and integrated them into a single model by assigning fusion weights. This proposed method allowed us to achieve 3rd place in the CVPR 2023 workshop of EPIC-SOUNDS Audio-Based Interaction Recognition Challenge.

Poisson Conjugate Prior for PHD Filtering based Track-Before-Detect Strategies in Radar Systems

A variety of filters with track-before-detect (TBD) strategies have been developed and applied to low signal-to-noise ratio (SNR) scenarios, including the probability hypothesis density (PHD) filter. Assumptions of the standard point measurement model based on detect-before-track (DBT) strategies are not suitable for the amplitude echo model based on TBD strategies. However, based on different models and unmatched assumptions, the measurement update formulas for DBT-PHD filter are just mechanically applied to existing TBD-PHD filters. In this paper, based on the Kullback-Leibler divergence minimization criterion, finite set statistics theory and rigorous Bayes rule, a principled closed-form solution of TBD-PHD filter is derived. Furthermore, we emphasize that PHD filter is conjugated to the Poisson prior based on TBD strategies. Next, a capping operation is devised to handle the divergence of target number estimation as SNR increases. Moreover, the sequential Monte Carlo implementations of dynamic and amplitude echo models are proposed for the radar system. Finally, Monte Carlo experiments exhibit good performance in Rayleigh noise and low SNR scenarios.

The Trajectory PHD Filter for Coexisting Point and Extended Target Tracking

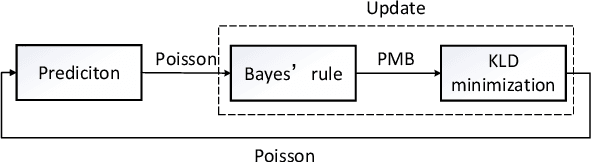
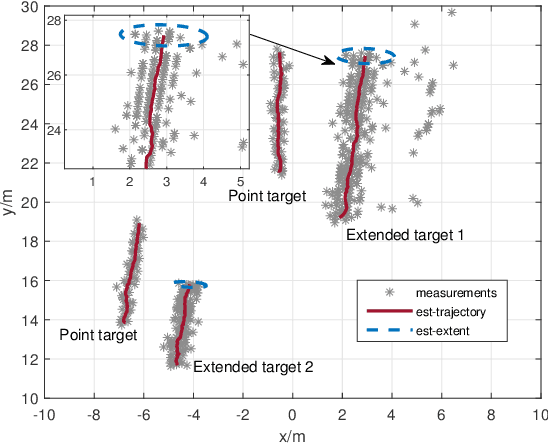
This paper develops a general trajectory probability hypothesis density (TPHD) filter, which uses a general density for target-generated measurements and is able to estimate trajectories of coexisting point and extended targets. First, we provide a derivation of this general TPHD filter based on finding the best Poisson posterior approximation by minimizing the Kullback-Leibler divergence, without using probability generating functionals. Second, we adopt an efficient implementation of this filter, where Gaussian densities correspond to point targets and Gamma Gaussian Inverse Wishart densities for extended targets. The L-scan approximation is also proposed as a simplified version to mitigate the huge computational cost. Simulation and experimental results show that the proposed filter is able to classify targets correctly and obtain accurate trajectory estimation.

Recent Advances for Quantum Neural Networks in Generative Learning

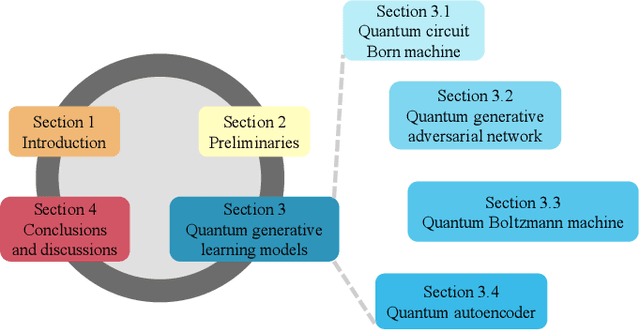
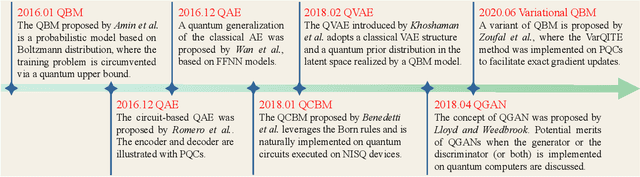
Quantum computers are next-generation devices that hold promise to perform calculations beyond the reach of classical computers. A leading method towards achieving this goal is through quantum machine learning, especially quantum generative learning. Due to the intrinsic probabilistic nature of quantum mechanics, it is reasonable to postulate that quantum generative learning models (QGLMs) may surpass their classical counterparts. As such, QGLMs are receiving growing attention from the quantum physics and computer science communities, where various QGLMs that can be efficiently implemented on near-term quantum machines with potential computational advantages are proposed. In this paper, we review the current progress of QGLMs from the perspective of machine learning. Particularly, we interpret these QGLMs, covering quantum circuit born machines, quantum generative adversarial networks, quantum Boltzmann machines, and quantum autoencoders, as the quantum extension of classical generative learning models. In this context, we explore their intrinsic relation and their fundamental differences. We further summarize the potential applications of QGLMs in both conventional machine learning tasks and quantum physics. Last, we discuss the challenges and further research directions for QGLMs.

Subspace-Based Detection and Localization in Distributed MIMO Radars

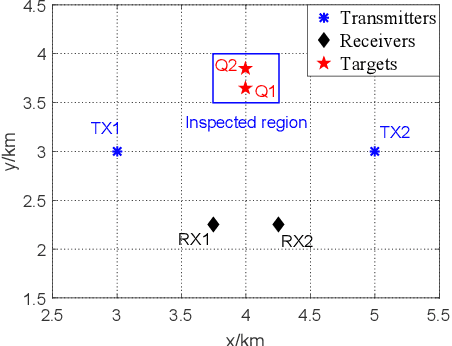
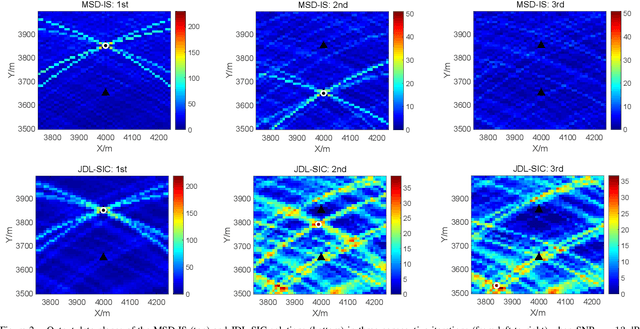
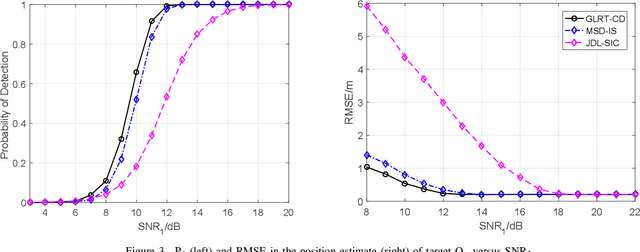
In this paper, we consider a distributed multiple-input multiple-output (MIMO) radar which radiates waveforms with non-ideal cross- and auto-correlation functions and derive a novel subspace-based procedure to detect and localize multiple prospective targets. The proposed solution solves a sequence of composite binary hypothesis testing problems by resorting to the generalized information criterion (GIC); in particular, at each step, it aims to detect and localize one additional target, upon removing the interference caused by the previously-detected targets. An illustrative example is provided.

Trajectory PHD Filter with Unknown Detection Profile and Clutter Rate

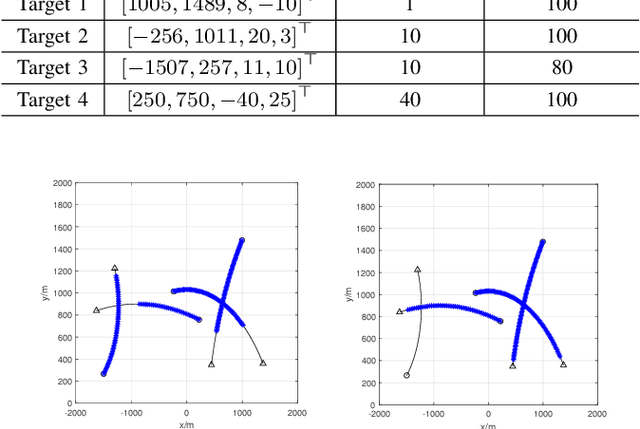
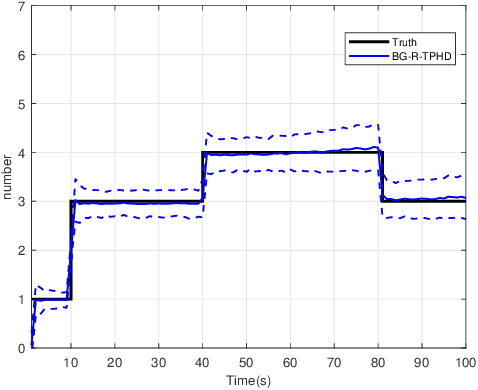
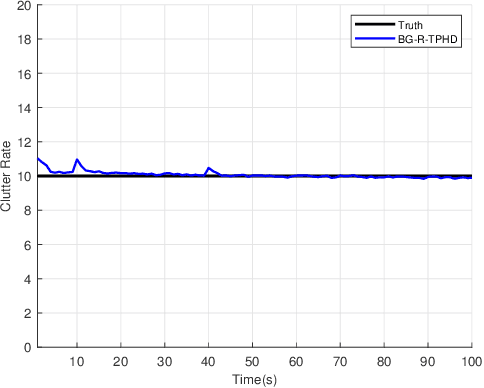
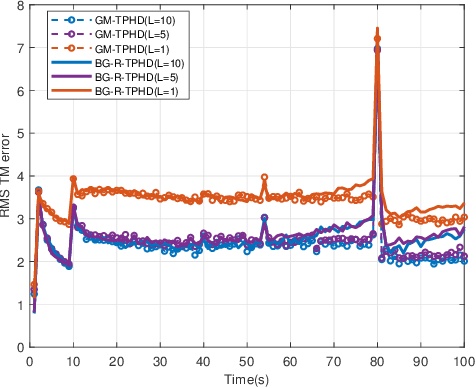
In this paper, we derive the robust TPHD (R-TPHD) filter, which can adaptively learn the unknown detection profile history and clutter rate. The R-TPHD filter is derived by obtaining the best Poisson posterior density approximation over trajectories on hybrid and augmented state space by minimizing the Kullback-Leibler divergence (KLD). Because of the huge computational burden and the short-term stability of the detection profile, we also propose the R-TPHD filter with unknown detection profile only at current time as an approximation. The Beta-Gaussian mixture model is proposed for the implementation, which is referred to as the BG-R-TPHD filter and we also propose a L-scan approximation for the BG-R-TPHD filter, which possesses lower computational burden.

Multi-target Joint Tracking and Classification Using the Trajectory PHD Filter

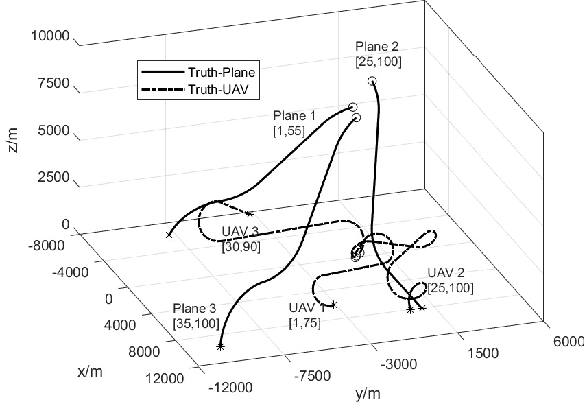
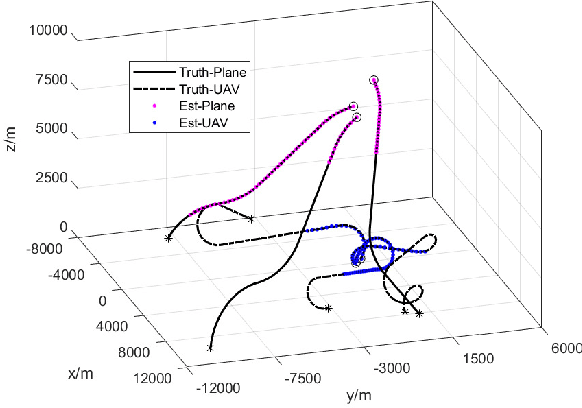
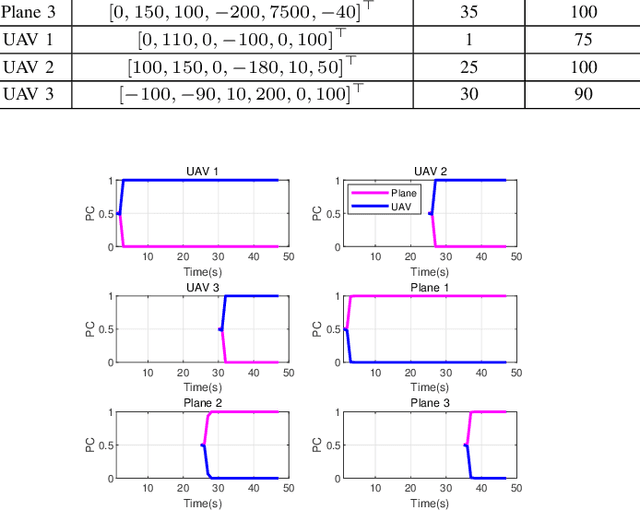
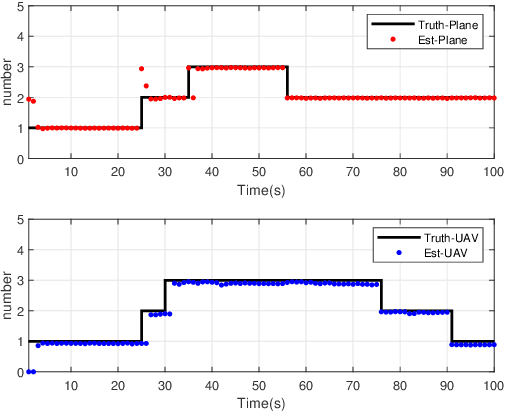
To account for joint tracking and classification (JTC) of multiple targets from observation sets in presence of detection uncertainty, noise and clutter, this paper develops a new trajectory probability hypothesis density (TPHD) filter, which is referred to as the JTC-TPHD filter. The JTC-TPHD filter classifies different targets based on their motion models and each target is assigned with multiple class hypotheses. By using this strategy, we can not only obtain the category information of the targets, but also a more accurate trajectory estimation than the traditional TPHD filter. The JTC-TPHD filter is derived by finding the best Poisson posterior approximation over trajectories on an augmented state space using the Kullback-Leibler divergence (KLD) minimization. The Gaussian mixture is adopted for the implementation, which is referred to as the GM-JTC-TPHD filter. The L-scan approximation is also presented for the GM-JTC-TPHD filter, which possesses lower computational burden. Simulation results show that the GM-JTC-TPHD filter can classify targets correctly and obtain accurate trajectory estimation.

Trajectory PHD and CPHD Filters with Unknown Detection Profile

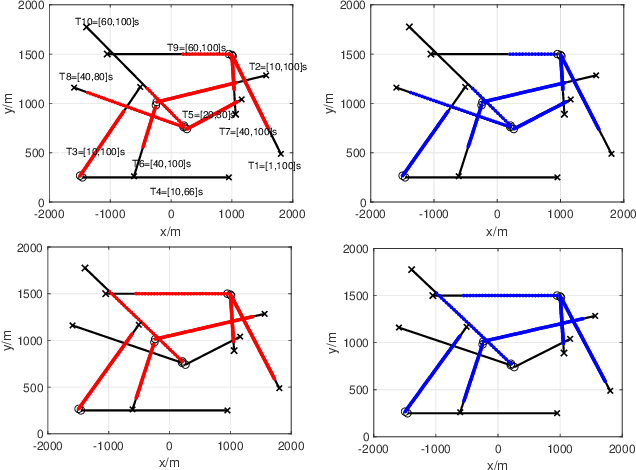
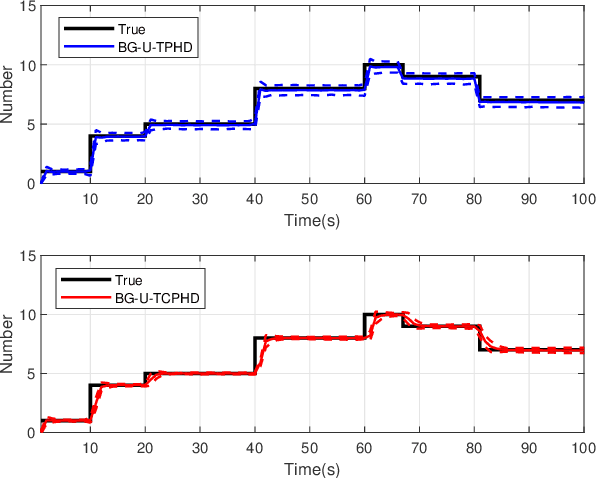
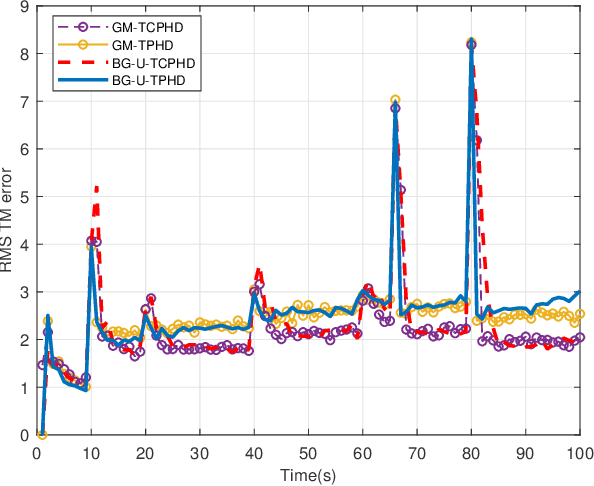
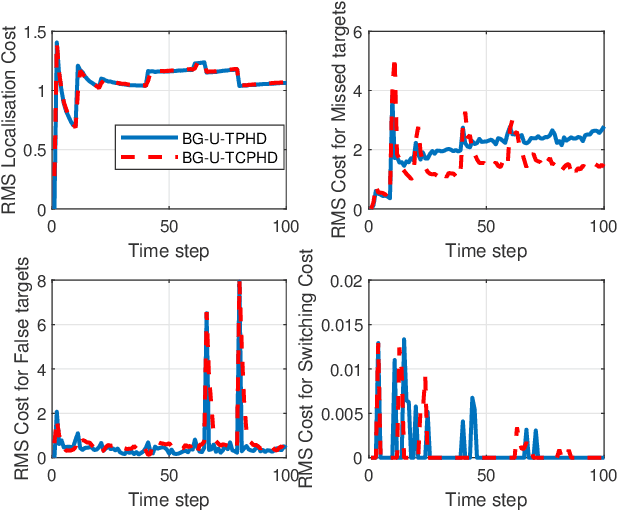
Compared to the probability hypothesis density (PHD) and cardinalized PHD (CPHD) filters, the trajectory PHD (TPHD) and trajectory CPHD (TCPHD) filters are for sets of trajectories, and thus are able to produce trajectory estimates with better estimation performance. In this paper, we develop the TPHD and TCPHD filters which can adaptively learn the history of the unknown target detection probability, and therefore they can perform more robustly in scenarios where targets are with unknown and time-varying detection probabilities. These filters are referred to as the unknown TPHD (U-TPHD) and unknown TCPHD (U-TCPHD) filters.By minimizing the Kullback-Leibler divergence (KLD), the U-TPHD and U-TCPHD filters can obtain, respectively, the best Poisson and independent identically distributed (IID) density approximations over the augmented sets of trajectories. For computational efficiency, we also propose the U-TPHD and U-TCPHD filters that only consider the unknown detection profile at the current time. Specifically, the Beta-Gaussian mixture method is adopted for the implementation of proposed filters, which are referred to as the BG-U-TPHD and BG-U-TCPHD filters. The L-scan approximations of these filters with much lower computational burden are also presented. Finally, various simulation results demonstrate that the BG-U-TPHD and BG-U-TCPHD filters can achieve robust tracking performance to adapt to unknown detection profile. Besides, it also shows that usually a small value of the L-scan approximation can achieve almost full efficiency of both filters but with a much lower computational costs.

Continuous-discrete multiple target tracking with out-of-sequence measurements

This paper derives the optimal Bayesian processing of an out-of-sequence (OOS) set of measurements in continuous-time for multiple target tracking. We consider a multi-target system modelled in continuous time that is discretised at the time steps when we receive the measurements, which are distributed according to the standard point target model. All information about this system at the sampled time steps is provided by the posterior density on the set of all trajectories. This density can be computed via the continuous-discrete trajectory Poisson multi-Bernoulli mixture (TPMBM) filter. When we receive an OOS measurement, the optimal Bayesian processing performs a retrodiction step that adds trajectory information at the OOS measurement time stamp followed by an update step. After the OOS measurement update, the posterior remains in TPMBM form. We also provide a computationally lighter alternative based on a trajectory Poisson multi-Bernoulli filter. The effectiveness of the two approaches to handle OOS measurements is evaluated via simulations.