Trajectory PHD and CPHD Filters with Unknown Detection Profile
Paper and Code
Nov 06, 2021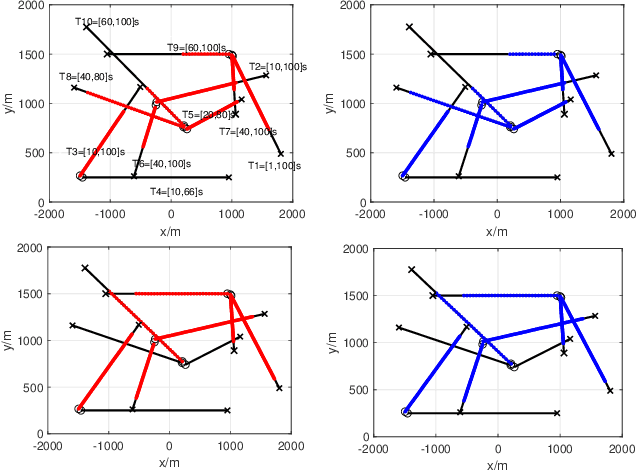
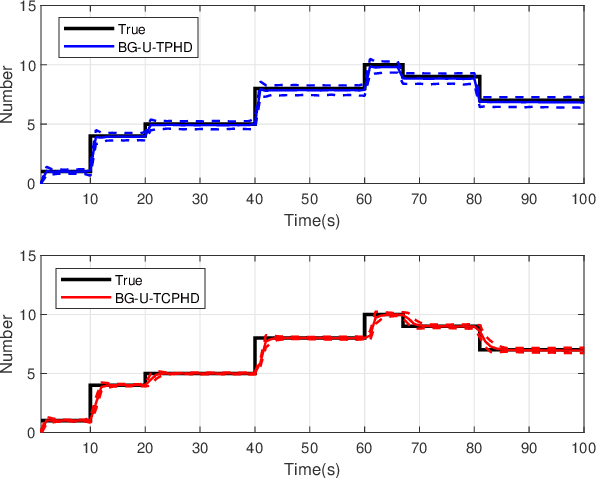
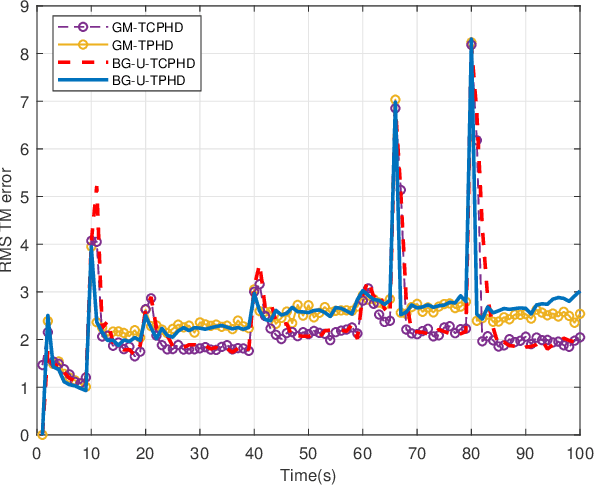
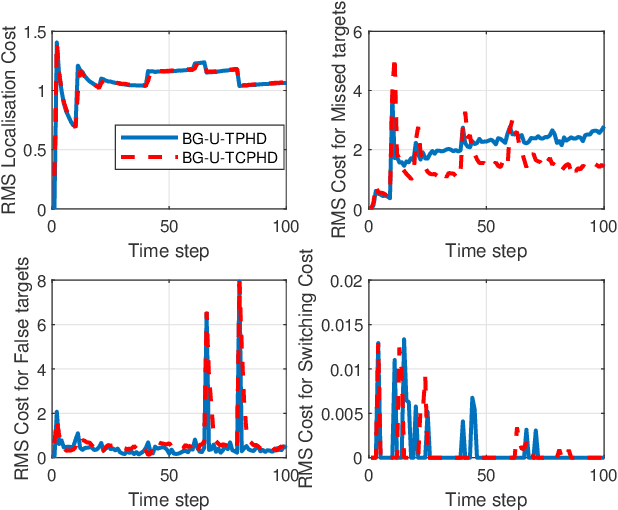
Compared to the probability hypothesis density (PHD) and cardinalized PHD (CPHD) filters, the trajectory PHD (TPHD) and trajectory CPHD (TCPHD) filters are for sets of trajectories, and thus are able to produce trajectory estimates with better estimation performance. In this paper, we develop the TPHD and TCPHD filters which can adaptively learn the history of the unknown target detection probability, and therefore they can perform more robustly in scenarios where targets are with unknown and time-varying detection probabilities. These filters are referred to as the unknown TPHD (U-TPHD) and unknown TCPHD (U-TCPHD) filters.By minimizing the Kullback-Leibler divergence (KLD), the U-TPHD and U-TCPHD filters can obtain, respectively, the best Poisson and independent identically distributed (IID) density approximations over the augmented sets of trajectories. For computational efficiency, we also propose the U-TPHD and U-TCPHD filters that only consider the unknown detection profile at the current time. Specifically, the Beta-Gaussian mixture method is adopted for the implementation of proposed filters, which are referred to as the BG-U-TPHD and BG-U-TCPHD filters. The L-scan approximations of these filters with much lower computational burden are also presented. Finally, various simulation results demonstrate that the BG-U-TPHD and BG-U-TCPHD filters can achieve robust tracking performance to adapt to unknown detection profile. Besides, it also shows that usually a small value of the L-scan approximation can achieve almost full efficiency of both filters but with a much lower computational costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge