A New Architecture for Neural Enhanced Multiobject Tracking

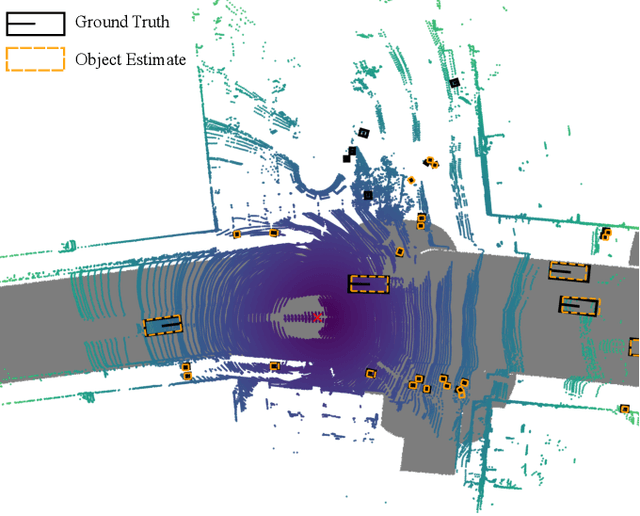
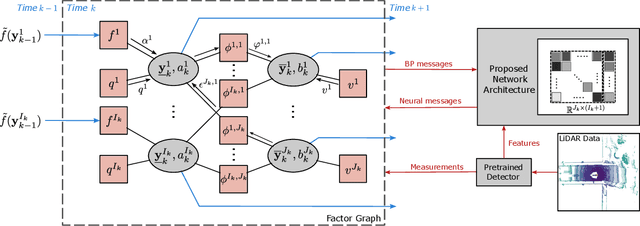
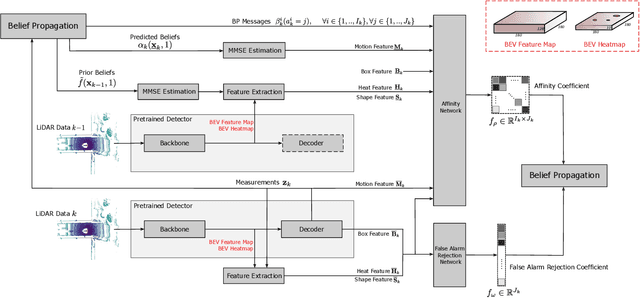
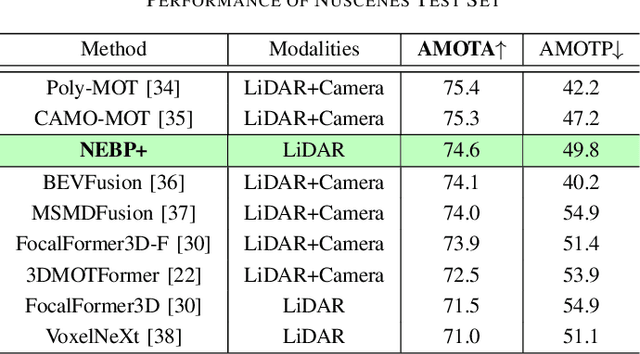
Multiobject tracking (MOT) is an important task in robotics, autonomous driving, and maritime surveillance. Traditional work on MOT is model-based and aims to establish algorithms in the framework of sequential Bayesian estimation. More recent methods are fully data-driven and rely on the training of neural networks. The two approaches have demonstrated advantages in certain scenarios. In particular, in problems where plenty of labeled data for the training of neural networks is available, data-driven MOT tends to have advantages compared to traditional methods. A natural thought is whether a general and efficient framework can integrate the two approaches. This paper advances a recently introduced hybrid model-based and data-driven method called neural-enhanced belief propagation (NEBP). Compared to existing work on NEBP for MOT, it introduces a novel neural architecture that can improve data association and new object initialization, two critical aspects of MOT. The proposed tracking method is leading the nuScenes LiDAR-only tracking challenge at the time of submission of this paper.

The Trajectory PHD Filter for Coexisting Point and Extended Target Tracking

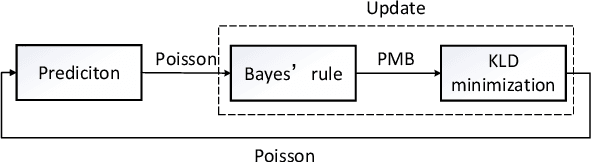
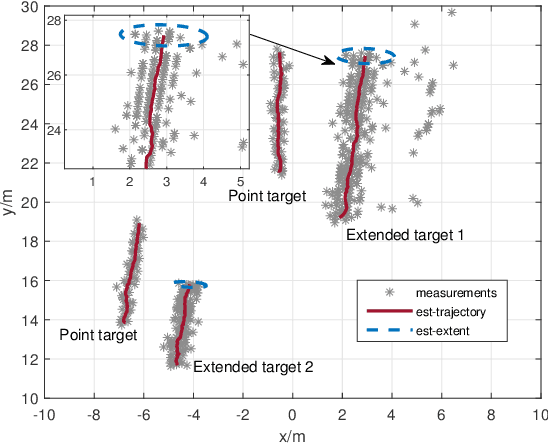
This paper develops a general trajectory probability hypothesis density (TPHD) filter, which uses a general density for target-generated measurements and is able to estimate trajectories of coexisting point and extended targets. First, we provide a derivation of this general TPHD filter based on finding the best Poisson posterior approximation by minimizing the Kullback-Leibler divergence, without using probability generating functionals. Second, we adopt an efficient implementation of this filter, where Gaussian densities correspond to point targets and Gamma Gaussian Inverse Wishart densities for extended targets. The L-scan approximation is also proposed as a simplified version to mitigate the huge computational cost. Simulation and experimental results show that the proposed filter is able to classify targets correctly and obtain accurate trajectory estimation.

Trajectory PHD Filter with Unknown Detection Profile and Clutter Rate

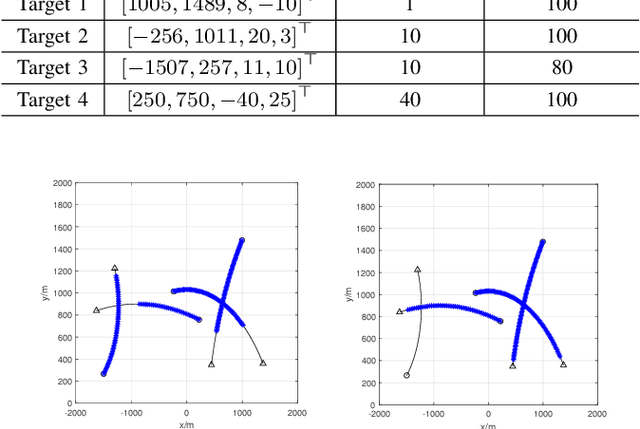
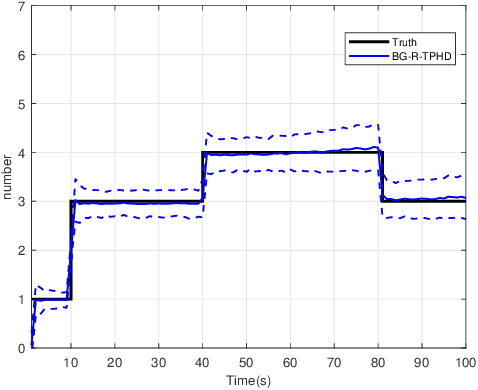
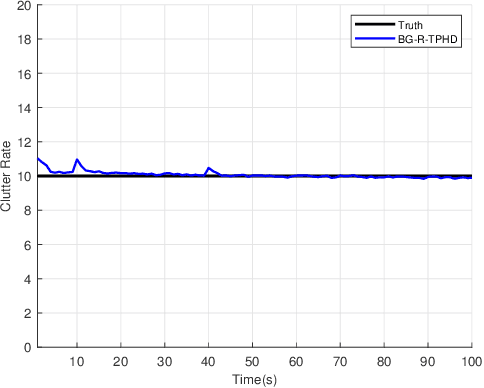
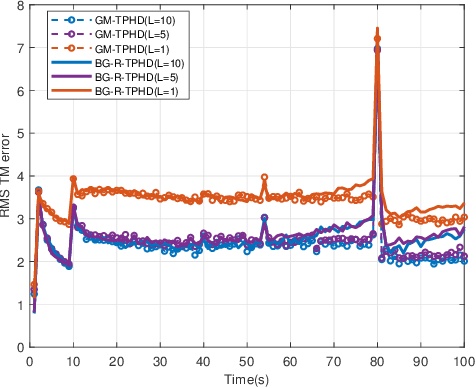
In this paper, we derive the robust TPHD (R-TPHD) filter, which can adaptively learn the unknown detection profile history and clutter rate. The R-TPHD filter is derived by obtaining the best Poisson posterior density approximation over trajectories on hybrid and augmented state space by minimizing the Kullback-Leibler divergence (KLD). Because of the huge computational burden and the short-term stability of the detection profile, we also propose the R-TPHD filter with unknown detection profile only at current time as an approximation. The Beta-Gaussian mixture model is proposed for the implementation, which is referred to as the BG-R-TPHD filter and we also propose a L-scan approximation for the BG-R-TPHD filter, which possesses lower computational burden.

Multi-target Joint Tracking and Classification Using the Trajectory PHD Filter

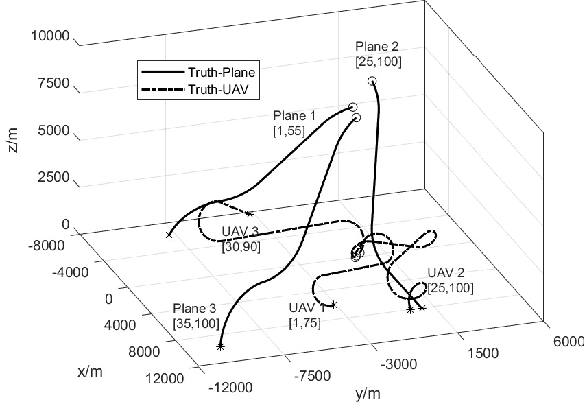
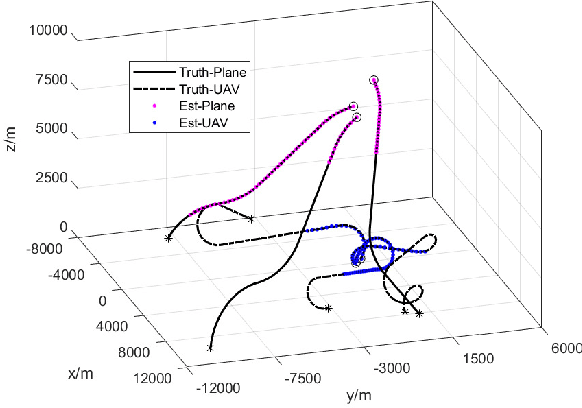
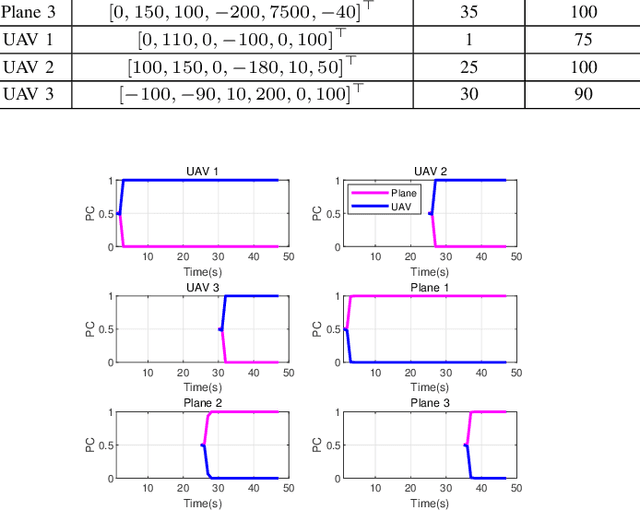
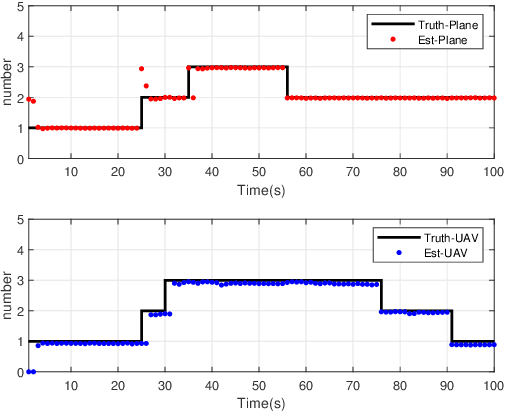
To account for joint tracking and classification (JTC) of multiple targets from observation sets in presence of detection uncertainty, noise and clutter, this paper develops a new trajectory probability hypothesis density (TPHD) filter, which is referred to as the JTC-TPHD filter. The JTC-TPHD filter classifies different targets based on their motion models and each target is assigned with multiple class hypotheses. By using this strategy, we can not only obtain the category information of the targets, but also a more accurate trajectory estimation than the traditional TPHD filter. The JTC-TPHD filter is derived by finding the best Poisson posterior approximation over trajectories on an augmented state space using the Kullback-Leibler divergence (KLD) minimization. The Gaussian mixture is adopted for the implementation, which is referred to as the GM-JTC-TPHD filter. The L-scan approximation is also presented for the GM-JTC-TPHD filter, which possesses lower computational burden. Simulation results show that the GM-JTC-TPHD filter can classify targets correctly and obtain accurate trajectory estimation.

Trajectory PHD and CPHD Filters with Unknown Detection Profile

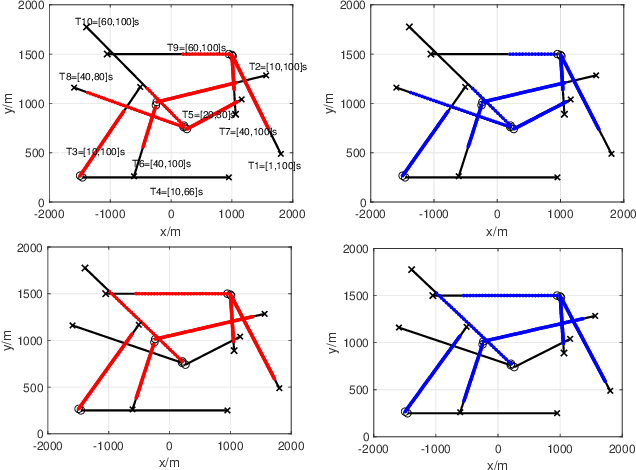
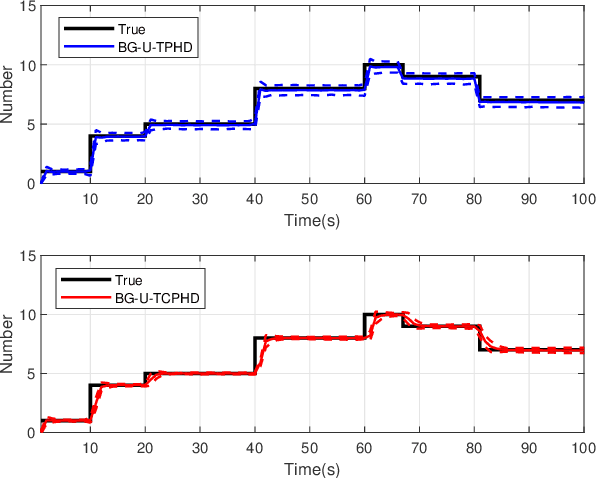
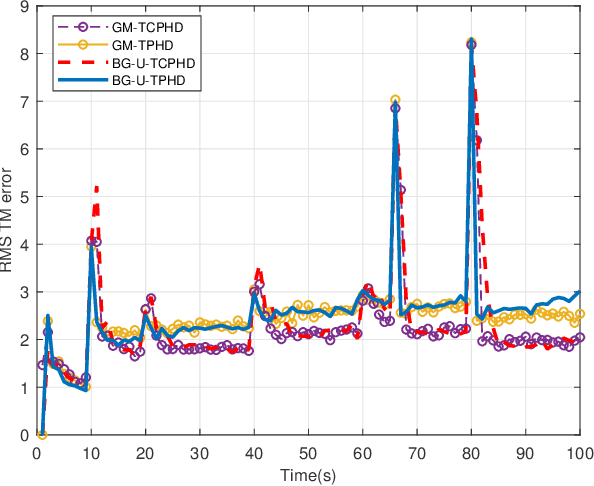
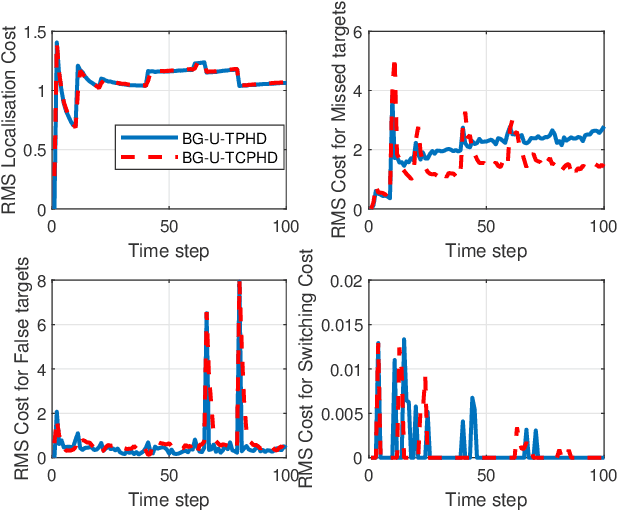
Compared to the probability hypothesis density (PHD) and cardinalized PHD (CPHD) filters, the trajectory PHD (TPHD) and trajectory CPHD (TCPHD) filters are for sets of trajectories, and thus are able to produce trajectory estimates with better estimation performance. In this paper, we develop the TPHD and TCPHD filters which can adaptively learn the history of the unknown target detection probability, and therefore they can perform more robustly in scenarios where targets are with unknown and time-varying detection probabilities. These filters are referred to as the unknown TPHD (U-TPHD) and unknown TCPHD (U-TCPHD) filters.By minimizing the Kullback-Leibler divergence (KLD), the U-TPHD and U-TCPHD filters can obtain, respectively, the best Poisson and independent identically distributed (IID) density approximations over the augmented sets of trajectories. For computational efficiency, we also propose the U-TPHD and U-TCPHD filters that only consider the unknown detection profile at the current time. Specifically, the Beta-Gaussian mixture method is adopted for the implementation of proposed filters, which are referred to as the BG-U-TPHD and BG-U-TCPHD filters. The L-scan approximations of these filters with much lower computational burden are also presented. Finally, various simulation results demonstrate that the BG-U-TPHD and BG-U-TCPHD filters can achieve robust tracking performance to adapt to unknown detection profile. Besides, it also shows that usually a small value of the L-scan approximation can achieve almost full efficiency of both filters but with a much lower computational costs.