Mx2M: Masked Cross-Modality Modeling in Domain Adaptation for 3D Semantic Segmentation

Existing methods of cross-modal domain adaptation for 3D semantic segmentation predict results only via 2D-3D complementarity that is obtained by cross-modal feature matching. However, as lacking supervision in the target domain, the complementarity is not always reliable. The results are not ideal when the domain gap is large. To solve the problem of lacking supervision, we introduce masked modeling into this task and propose a method Mx2M, which utilizes masked cross-modality modeling to reduce the large domain gap. Our Mx2M contains two components. One is the core solution, cross-modal removal and prediction (xMRP), which makes the Mx2M adapt to various scenarios and provides cross-modal self-supervision. The other is a new way of cross-modal feature matching, the dynamic cross-modal filter (DxMF) that ensures the whole method dynamically uses more suitable 2D-3D complementarity. Evaluation of the Mx2M on three DA scenarios, including Day/Night, USA/Singapore, and A2D2/SemanticKITTI, brings large improvements over previous methods on many metrics.

Trajectory PHD Filter with Unknown Detection Profile and Clutter Rate

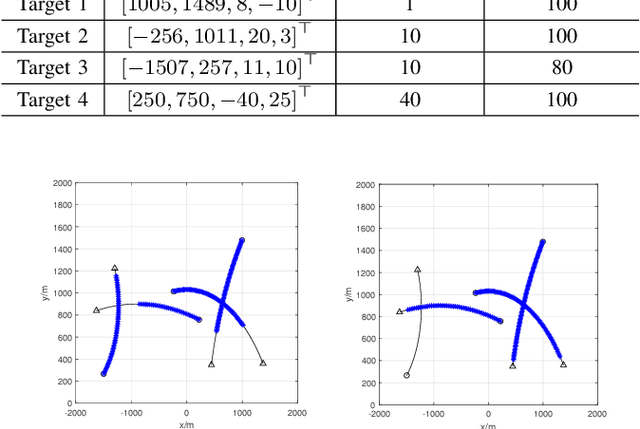
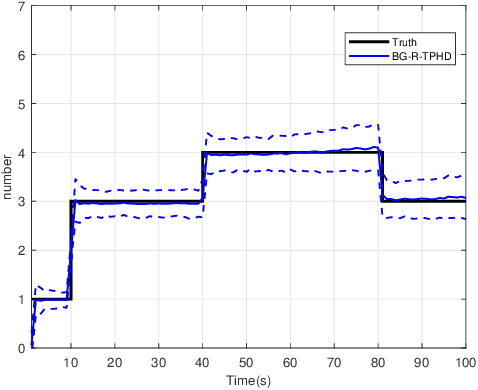
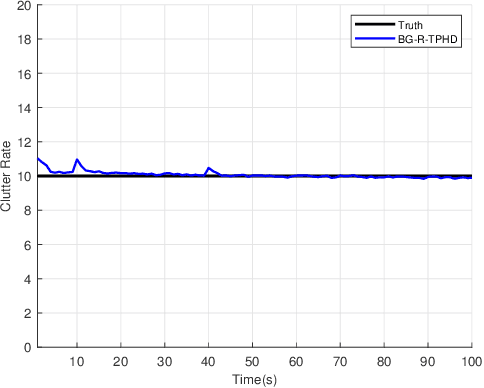
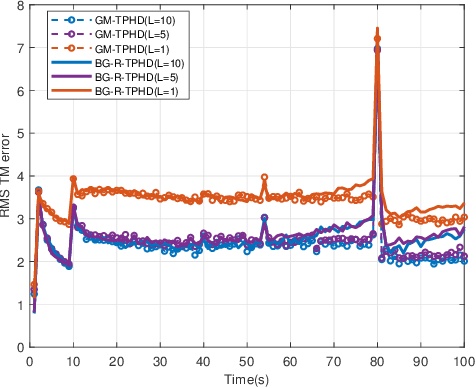
In this paper, we derive the robust TPHD (R-TPHD) filter, which can adaptively learn the unknown detection profile history and clutter rate. The R-TPHD filter is derived by obtaining the best Poisson posterior density approximation over trajectories on hybrid and augmented state space by minimizing the Kullback-Leibler divergence (KLD). Because of the huge computational burden and the short-term stability of the detection profile, we also propose the R-TPHD filter with unknown detection profile only at current time as an approximation. The Beta-Gaussian mixture model is proposed for the implementation, which is referred to as the BG-R-TPHD filter and we also propose a L-scan approximation for the BG-R-TPHD filter, which possesses lower computational burden.

Multi-target Joint Tracking and Classification Using the Trajectory PHD Filter

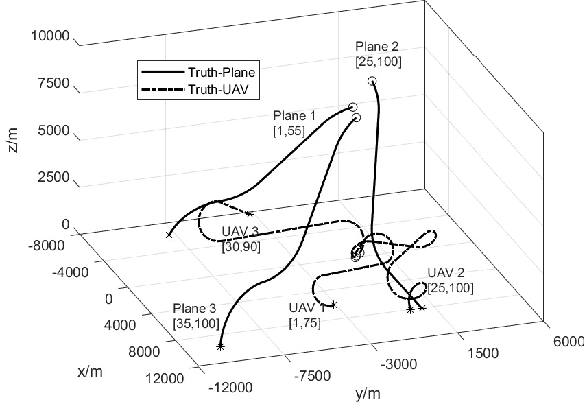
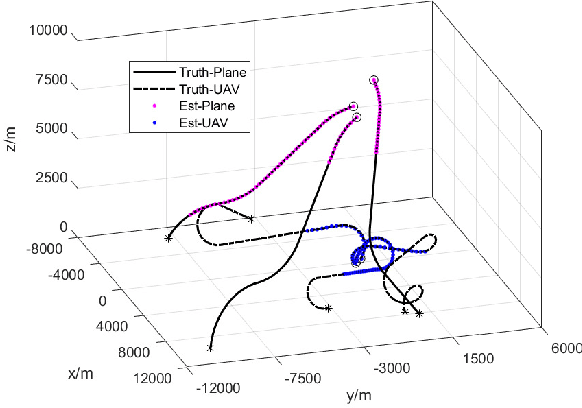
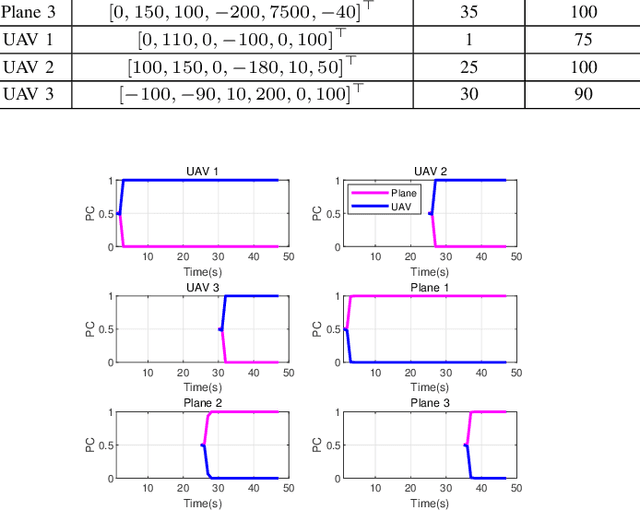
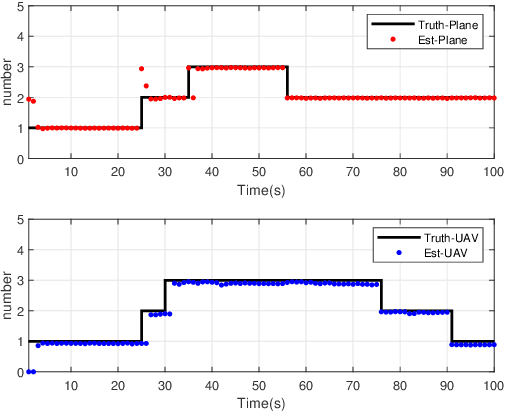
To account for joint tracking and classification (JTC) of multiple targets from observation sets in presence of detection uncertainty, noise and clutter, this paper develops a new trajectory probability hypothesis density (TPHD) filter, which is referred to as the JTC-TPHD filter. The JTC-TPHD filter classifies different targets based on their motion models and each target is assigned with multiple class hypotheses. By using this strategy, we can not only obtain the category information of the targets, but also a more accurate trajectory estimation than the traditional TPHD filter. The JTC-TPHD filter is derived by finding the best Poisson posterior approximation over trajectories on an augmented state space using the Kullback-Leibler divergence (KLD) minimization. The Gaussian mixture is adopted for the implementation, which is referred to as the GM-JTC-TPHD filter. The L-scan approximation is also presented for the GM-JTC-TPHD filter, which possesses lower computational burden. Simulation results show that the GM-JTC-TPHD filter can classify targets correctly and obtain accurate trajectory estimation.

Trajectory PHD and CPHD Filters with Unknown Detection Profile

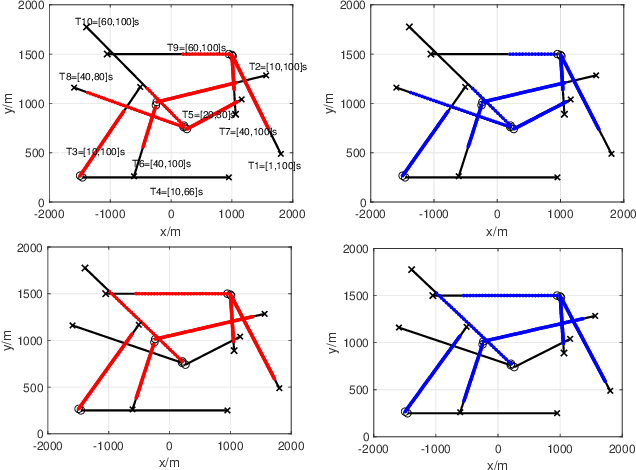
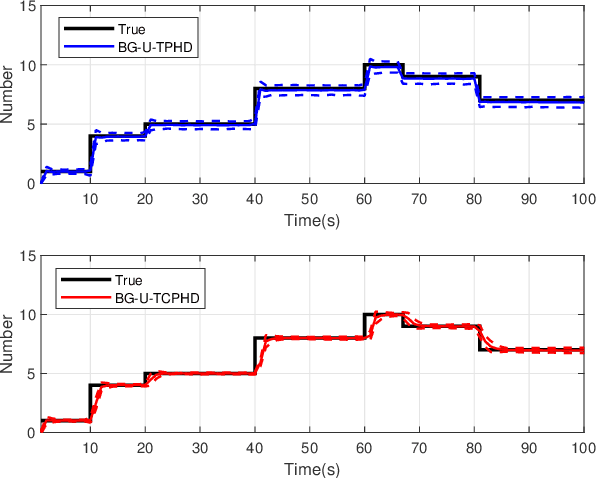
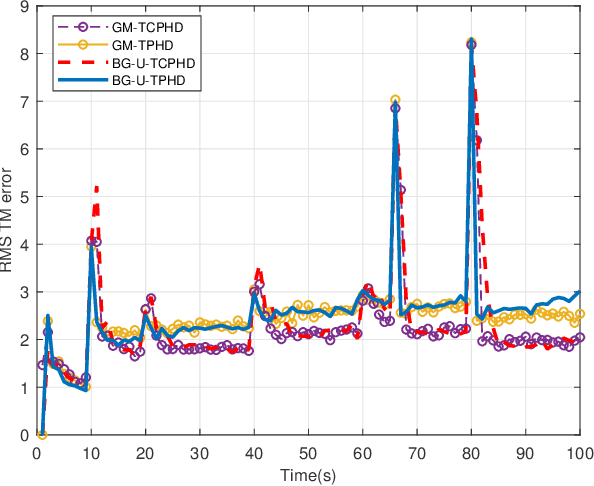
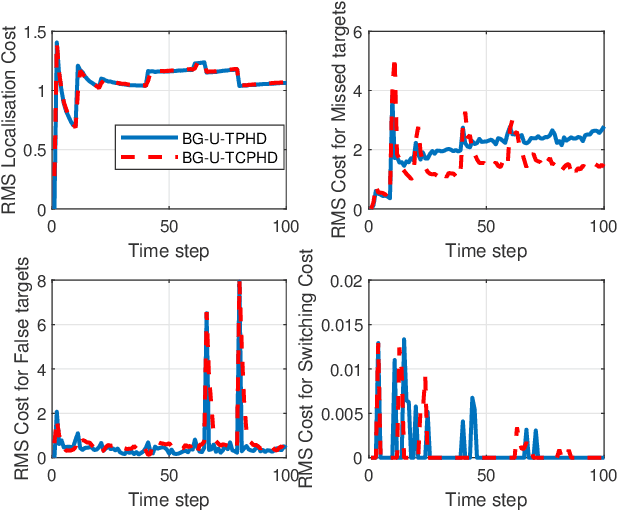
Compared to the probability hypothesis density (PHD) and cardinalized PHD (CPHD) filters, the trajectory PHD (TPHD) and trajectory CPHD (TCPHD) filters are for sets of trajectories, and thus are able to produce trajectory estimates with better estimation performance. In this paper, we develop the TPHD and TCPHD filters which can adaptively learn the history of the unknown target detection probability, and therefore they can perform more robustly in scenarios where targets are with unknown and time-varying detection probabilities. These filters are referred to as the unknown TPHD (U-TPHD) and unknown TCPHD (U-TCPHD) filters.By minimizing the Kullback-Leibler divergence (KLD), the U-TPHD and U-TCPHD filters can obtain, respectively, the best Poisson and independent identically distributed (IID) density approximations over the augmented sets of trajectories. For computational efficiency, we also propose the U-TPHD and U-TCPHD filters that only consider the unknown detection profile at the current time. Specifically, the Beta-Gaussian mixture method is adopted for the implementation of proposed filters, which are referred to as the BG-U-TPHD and BG-U-TCPHD filters. The L-scan approximations of these filters with much lower computational burden are also presented. Finally, various simulation results demonstrate that the BG-U-TPHD and BG-U-TCPHD filters can achieve robust tracking performance to adapt to unknown detection profile. Besides, it also shows that usually a small value of the L-scan approximation can achieve almost full efficiency of both filters but with a much lower computational costs.