Trajectory PHD Filter with Unknown Detection Profile and Clutter Rate
Paper and Code
Nov 06, 2021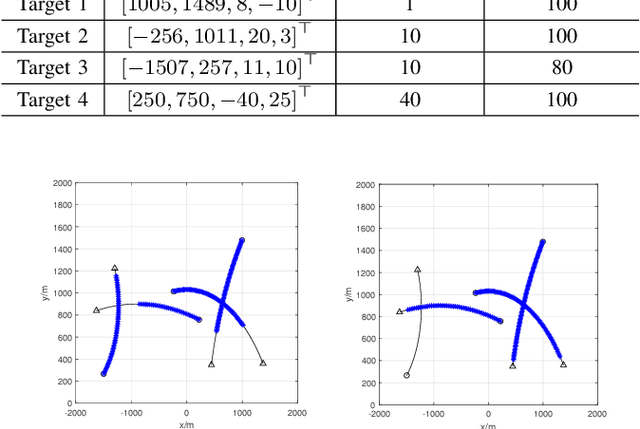
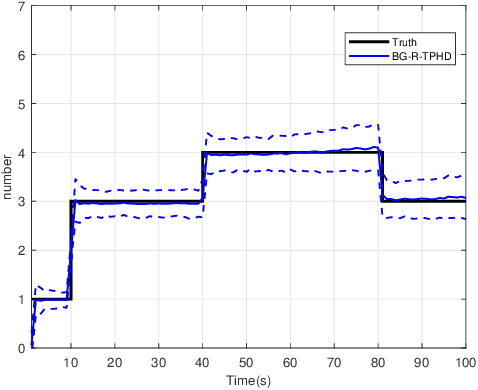
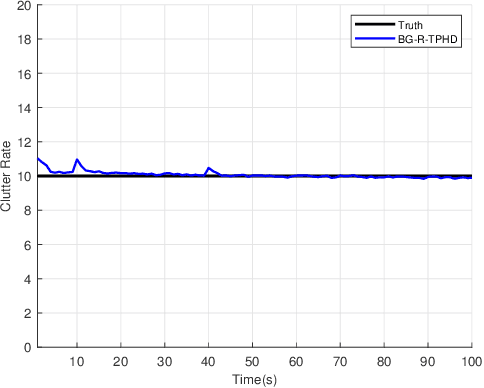
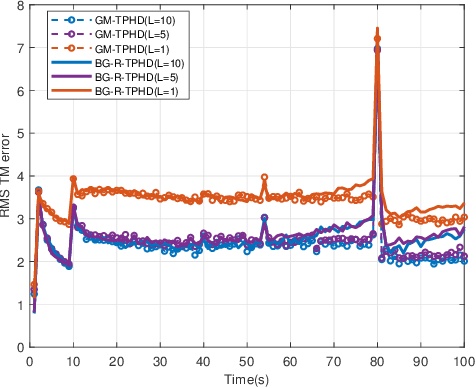
In this paper, we derive the robust TPHD (R-TPHD) filter, which can adaptively learn the unknown detection profile history and clutter rate. The R-TPHD filter is derived by obtaining the best Poisson posterior density approximation over trajectories on hybrid and augmented state space by minimizing the Kullback-Leibler divergence (KLD). Because of the huge computational burden and the short-term stability of the detection profile, we also propose the R-TPHD filter with unknown detection profile only at current time as an approximation. The Beta-Gaussian mixture model is proposed for the implementation, which is referred to as the BG-R-TPHD filter and we also propose a L-scan approximation for the BG-R-TPHD filter, which possesses lower computational burden.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge