The Trajectory PHD Filter for Coexisting Point and Extended Target Tracking
Paper and Code
Oct 07, 2022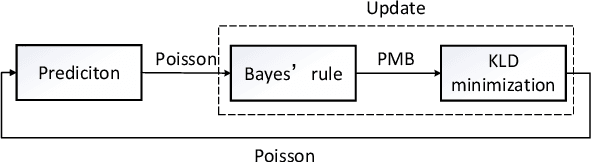
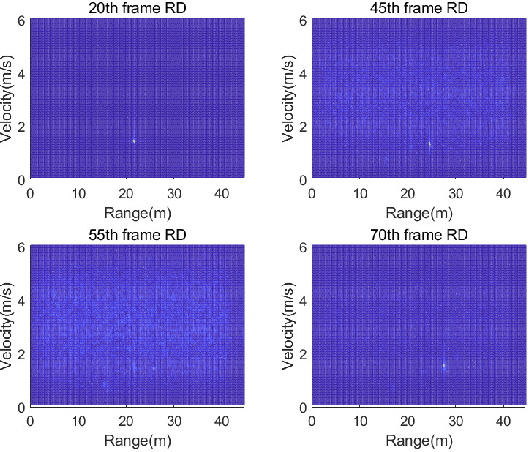
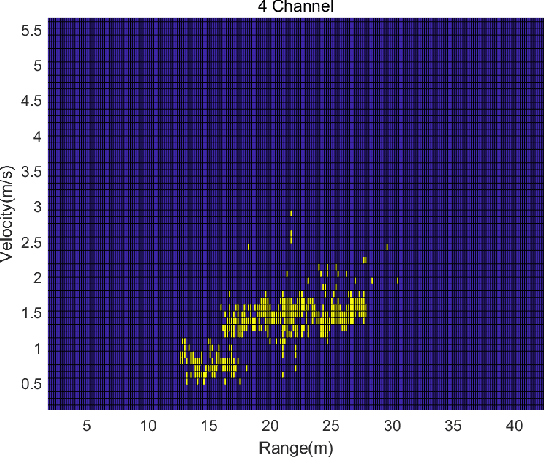
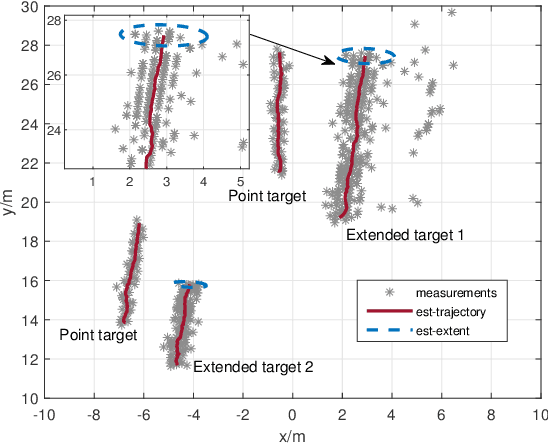
This paper develops a general trajectory probability hypothesis density (TPHD) filter, which uses a general density for target-generated measurements and is able to estimate trajectories of coexisting point and extended targets. First, we provide a derivation of this general TPHD filter based on finding the best Poisson posterior approximation by minimizing the Kullback-Leibler divergence, without using probability generating functionals. Second, we adopt an efficient implementation of this filter, where Gaussian densities correspond to point targets and Gamma Gaussian Inverse Wishart densities for extended targets. The L-scan approximation is also proposed as a simplified version to mitigate the huge computational cost. Simulation and experimental results show that the proposed filter is able to classify targets correctly and obtain accurate trajectory estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge