Learning Identifiable Factorized Causal Representations of Cellular Responses

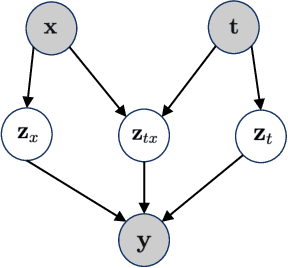
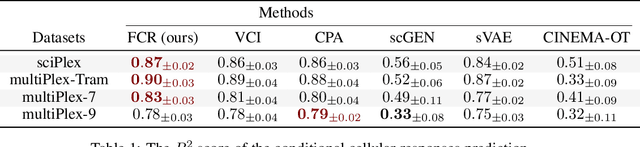
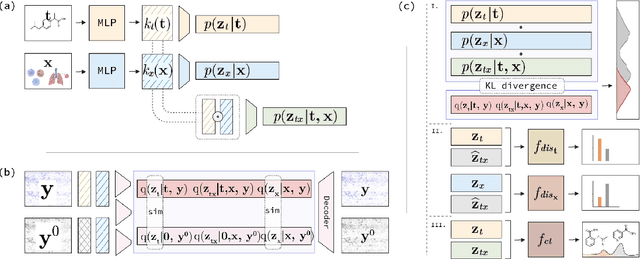
The study of cells and their responses to genetic or chemical perturbations promises to accelerate the discovery of therapeutic targets. However, designing adequate and insightful models for such data is difficult because the response of a cell to perturbations essentially depends on its biological context (e.g., genetic background or cell type). For example, while discovering therapeutic targets, one may want to enrich for drugs that specifically target a certain cell type. This challenge emphasizes the need for methods that explicitly take into account potential interactions between drugs and contexts. Towards this goal, we propose a novel Factorized Causal Representation (FCR) learning method that reveals causal structure in single-cell perturbation data from several cell lines. Based on the framework of identifiable deep generative models, FCR learns multiple cellular representations that are disentangled, comprised of covariate-specific ($\mathbf{z}_x$), treatment-specific ($\mathbf{z}_{t}$), and interaction-specific ($\mathbf{z}_{tx}$) blocks. Based on recent advances in non-linear ICA theory, we prove the component-wise identifiability of $\mathbf{z}_{tx}$ and block-wise identifiability of $\mathbf{z}_t$ and $\mathbf{z}_x$. Then, we present our implementation of FCR, and empirically demonstrate that it outperforms state-of-the-art baselines in various tasks across four single-cell datasets.

Poisson Conjugate Prior for PHD Filtering based Track-Before-Detect Strategies in Radar Systems

A variety of filters with track-before-detect (TBD) strategies have been developed and applied to low signal-to-noise ratio (SNR) scenarios, including the probability hypothesis density (PHD) filter. Assumptions of the standard point measurement model based on detect-before-track (DBT) strategies are not suitable for the amplitude echo model based on TBD strategies. However, based on different models and unmatched assumptions, the measurement update formulas for DBT-PHD filter are just mechanically applied to existing TBD-PHD filters. In this paper, based on the Kullback-Leibler divergence minimization criterion, finite set statistics theory and rigorous Bayes rule, a principled closed-form solution of TBD-PHD filter is derived. Furthermore, we emphasize that PHD filter is conjugated to the Poisson prior based on TBD strategies. Next, a capping operation is devised to handle the divergence of target number estimation as SNR increases. Moreover, the sequential Monte Carlo implementations of dynamic and amplitude echo models are proposed for the radar system. Finally, Monte Carlo experiments exhibit good performance in Rayleigh noise and low SNR scenarios.

Decomposable Sparse Tensor on Tensor Regression

Most regularized tensor regression research focuses on tensors predictors with scalars responses or vectors predictors to tensors responses. We consider the sparse low rank tensor on tensor regression where predictors $\mathcal{X}$ and responses $\mathcal{Y}$ are both high-dimensional tensors. By demonstrating that the general inner product or the contracted product on a unit rank tensor can be decomposed into standard inner products and outer products, the problem can be simply transformed into a tensor to scalar regression followed by a tensor decomposition. So we propose a fast solution based on stagewise search composed by contraction part and generation part which are optimized alternatively. We successfully demonstrate our method can out perform current methods in terms of accuracy and predictors selection by effectively incorporating the structural information.

COEM: Cross-Modal Embedding for MetaCell Identification

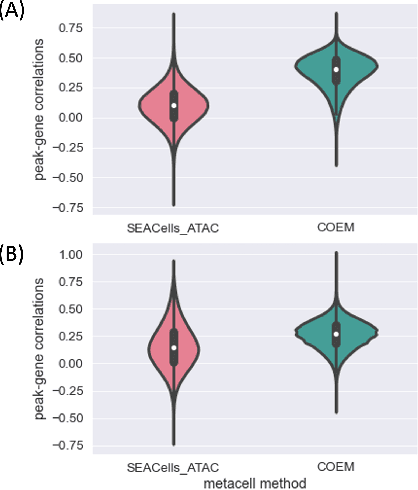
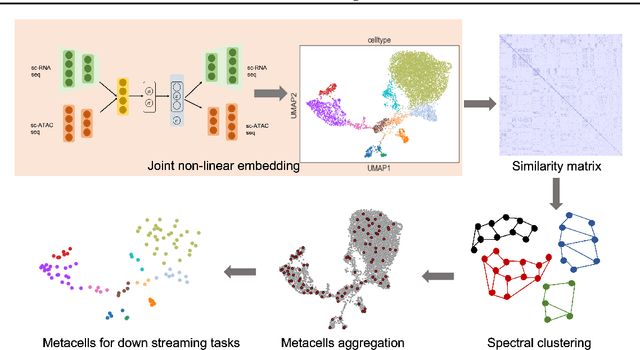
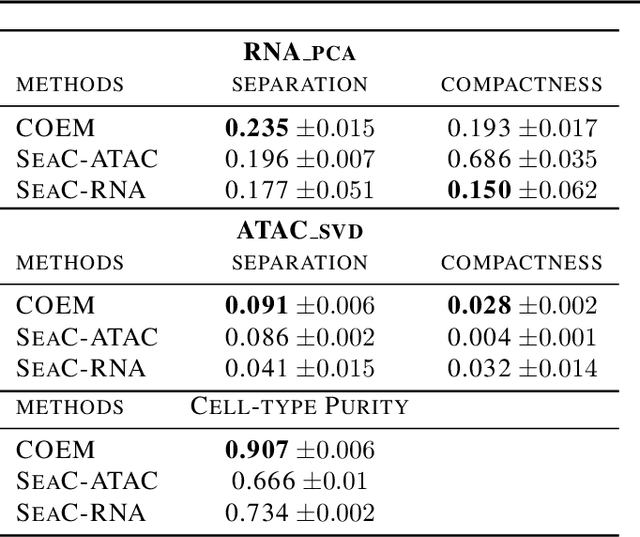
Metacells are disjoint and homogeneous groups of single-cell profiles, representing discrete and highly granular cell states. Existing metacell algorithms tend to use only one modality to infer metacells, even though single-cell multi-omics datasets profile multiple molecular modalities within the same cell. Here, we present \textbf{C}ross-M\textbf{O}dal \textbf{E}mbedding for \textbf{M}etaCell Identification (COEM), which utilizes an embedded space leveraging the information of both scATAC-seq and scRNA-seq to perform aggregation, balancing the trade-off between fine resolution and sufficient sequencing coverage. COEM outperforms the state-of-the-art method SEACells by efficiently identifying accurate and well-separated metacells across datasets with continuous and discrete cell types. Furthermore, COEM significantly improves peak-to-gene association analyses, and facilitates complex gene regulatory inference tasks.