Decomposable Sparse Tensor on Tensor Regression

Most regularized tensor regression research focuses on tensors predictors with scalars responses or vectors predictors to tensors responses. We consider the sparse low rank tensor on tensor regression where predictors $\mathcal{X}$ and responses $\mathcal{Y}$ are both high-dimensional tensors. By demonstrating that the general inner product or the contracted product on a unit rank tensor can be decomposed into standard inner products and outer products, the problem can be simply transformed into a tensor to scalar regression followed by a tensor decomposition. So we propose a fast solution based on stagewise search composed by contraction part and generation part which are optimized alternatively. We successfully demonstrate our method can out perform current methods in terms of accuracy and predictors selection by effectively incorporating the structural information.

Sampling Through the Lens of Sequential Decision Making

Sampling is ubiquitous in machine learning methodologies. Due to the growth of large datasets and model complexity, we want to learn and adapt the sampling process while training a representation. Towards achieving this grand goal, a variety of sampling techniques have been proposed. However, most of them either use a fixed sampling scheme or adjust the sampling scheme based on simple heuristics. They cannot choose the best sample for model training in different stages. Inspired by "Think, Fast and Slow" (System 1 and System 2) in cognitive science, we propose a reward-guided sampling strategy called Adaptive Sample with Reward (ASR) to tackle this challenge. To the best of our knowledge, this is the first work utilizing reinforcement learning (RL) to address the sampling problem in representation learning. Our approach optimally adjusts the sampling process to achieve optimal performance. We explore geographical relationships among samples by distance-based sampling to maximize overall cumulative reward. We apply ASR to the long-standing sampling problems in similarity-based loss functions. Empirical results in information retrieval and clustering demonstrate ASR's superb performance across different datasets. We also discuss an engrossing phenomenon which we name as "ASR gravity well" in experiments.

COEM: Cross-Modal Embedding for MetaCell Identification

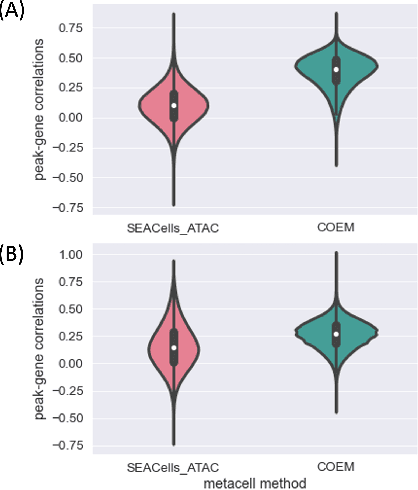
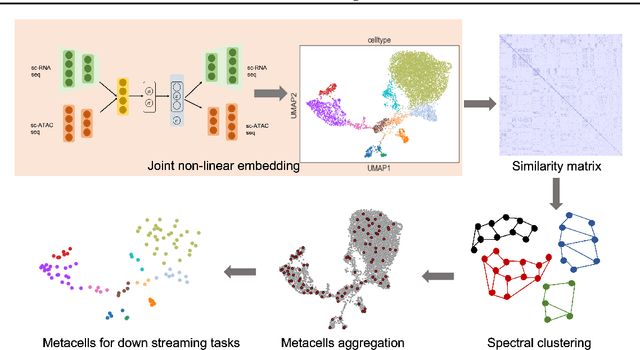
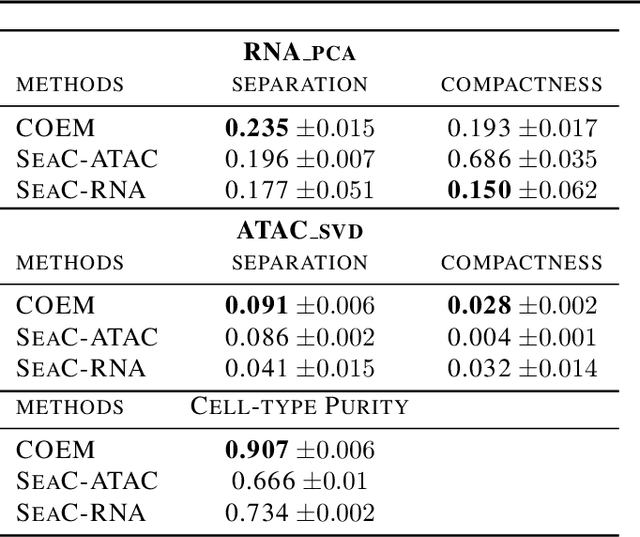
Metacells are disjoint and homogeneous groups of single-cell profiles, representing discrete and highly granular cell states. Existing metacell algorithms tend to use only one modality to infer metacells, even though single-cell multi-omics datasets profile multiple molecular modalities within the same cell. Here, we present \textbf{C}ross-M\textbf{O}dal \textbf{E}mbedding for \textbf{M}etaCell Identification (COEM), which utilizes an embedded space leveraging the information of both scATAC-seq and scRNA-seq to perform aggregation, balancing the trade-off between fine resolution and sufficient sequencing coverage. COEM outperforms the state-of-the-art method SEACells by efficiently identifying accurate and well-separated metacells across datasets with continuous and discrete cell types. Furthermore, COEM significantly improves peak-to-gene association analyses, and facilitates complex gene regulatory inference tasks.