Unleashing High-Quality Image Generation in Diffusion Sampling Using Second-Order Levenberg-Marquardt-Langevin

The diffusion models (DMs) have demonstrated the remarkable capability of generating images via learning the noised score function of data distribution. Current DM sampling techniques typically rely on first-order Langevin dynamics at each noise level, with efforts concentrated on refining inter-level denoising strategies. While leveraging additional second-order Hessian geometry to enhance the sampling quality of Langevin is a common practice in Markov chain Monte Carlo (MCMC), the naive attempts to utilize Hessian geometry in high-dimensional DMs lead to quadratic-complexity computational costs, rendering them non-scalable. In this work, we introduce a novel Levenberg-Marquardt-Langevin (LML) method that approximates the diffusion Hessian geometry in a training-free manner, drawing inspiration from the celebrated Levenberg-Marquardt optimization algorithm. Our approach introduces two key innovations: (1) A low-rank approximation of the diffusion Hessian, leveraging the DMs' inherent structure and circumventing explicit quadratic-complexity computations; (2) A damping mechanism to stabilize the approximated Hessian. This LML approximated Hessian geometry enables the diffusion sampling to execute more accurate steps and improve the image generation quality. We further conduct a theoretical analysis to substantiate the approximation error bound of low-rank approximation and the convergence property of the damping mechanism. Extensive experiments across multiple pretrained DMs validate that the LML method significantly improves image generation quality, with negligible computational overhead.

Efficiently Access Diffusion Fisher: Within the Outer Product Span Space

Recent Diffusion models (DMs) advancements have explored incorporating the second-order diffusion Fisher information (DF), defined as the negative Hessian of log density, into various downstream tasks and theoretical analysis. However, current practices typically approximate the diffusion Fisher by applying auto-differentiation to the learned score network. This black-box method, though straightforward, lacks any accuracy guarantee and is time-consuming. In this paper, we show that the diffusion Fisher actually resides within a space spanned by the outer products of score and initial data. Based on the outer-product structure, we develop two efficient approximation algorithms to access the trace and matrix-vector multiplication of DF, respectively. These algorithms bypass the auto-differentiation operations with time-efficient vector-product calculations. Furthermore, we establish the approximation error bounds for the proposed algorithms. Experiments in likelihood evaluation and adjoint optimization demonstrate the superior accuracy and reduced computational cost of our proposed algorithms. Additionally, based on the novel outer-product formulation of DF, we design the first numerical verification experiment for the optimal transport property of the general PF-ODE deduced map.

Quantum Compiling with Reinforcement Learning on a Superconducting Processor

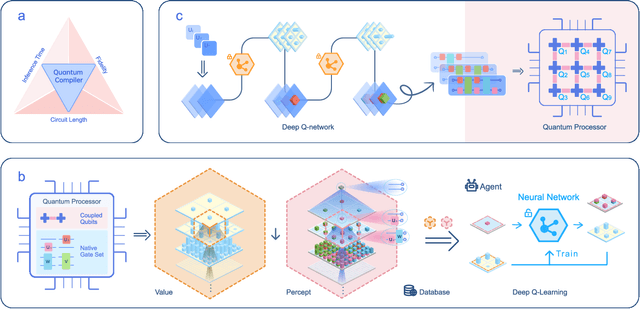
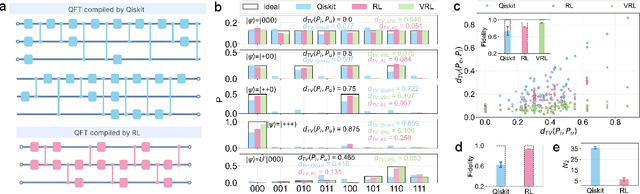
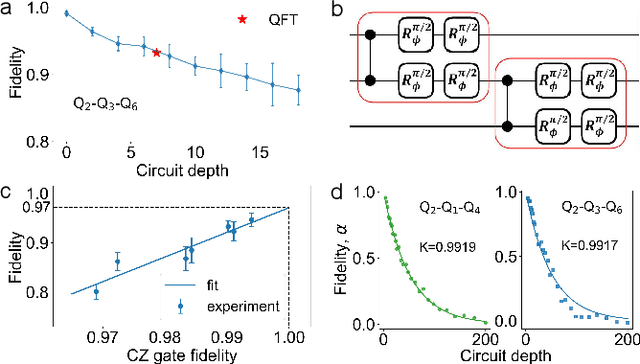
To effectively implement quantum algorithms on noisy intermediate-scale quantum (NISQ) processors is a central task in modern quantum technology. NISQ processors feature tens to a few hundreds of noisy qubits with limited coherence times and gate operations with errors, so NISQ algorithms naturally require employing circuits of short lengths via quantum compilation. Here, we develop a reinforcement learning (RL)-based quantum compiler for a superconducting processor and demonstrate its capability of discovering novel and hardware-amenable circuits with short lengths. We show that for the three-qubit quantum Fourier transformation, a compiled circuit using only seven CZ gates with unity circuit fidelity can be achieved. The compiler is also able to find optimal circuits under device topological constraints, with lengths considerably shorter than those by the conventional method. Our study exemplifies the codesign of the software with hardware for efficient quantum compilation, offering valuable insights for the advancement of RL-based compilers.

HGE: Embedding Temporal Knowledge Graphs in a Product Space of Heterogeneous Geometric Subspaces

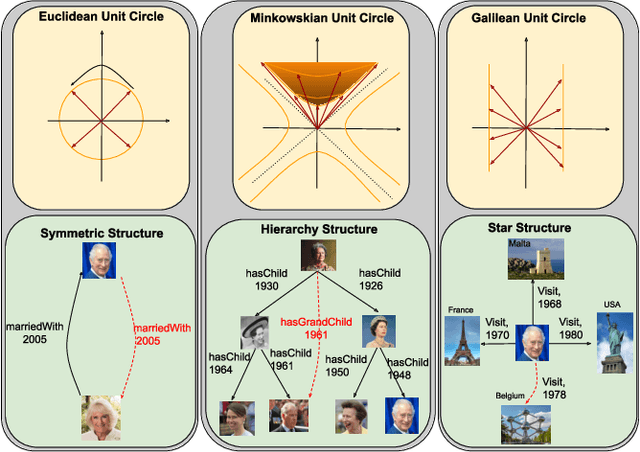
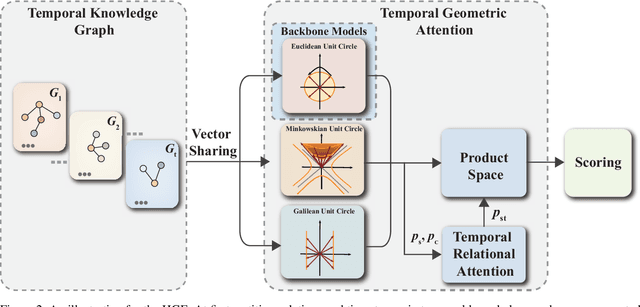
Temporal knowledge graphs represent temporal facts $(s,p,o,\tau)$ relating a subject $s$ and an object $o$ via a relation label $p$ at time $\tau$, where $\tau$ could be a time point or time interval. Temporal knowledge graphs may exhibit static temporal patterns at distinct points in time and dynamic temporal patterns between different timestamps. In order to learn a rich set of static and dynamic temporal patterns and apply them for inference, several embedding approaches have been suggested in the literature. However, as most of them resort to single underlying embedding spaces, their capability to model all kinds of temporal patterns was severely limited by having to adhere to the geometric property of their one embedding space. We lift this limitation by an embedding approach that maps temporal facts into a product space of several heterogeneous geometric subspaces with distinct geometric properties, i.e.\ Complex, Dual, and Split-complex spaces. In addition, we propose a temporal-geometric attention mechanism to integrate information from different geometric subspaces conveniently according to the captured relational and temporal information. Experimental results on standard temporal benchmark datasets favorably evaluate our approach against state-of-the-art models.

Semi-Supervised Panoptic Narrative Grounding

Despite considerable progress, the advancement of Panoptic Narrative Grounding (PNG) remains hindered by costly annotations. In this paper, we introduce a novel Semi-Supervised Panoptic Narrative Grounding (SS-PNG) learning scheme, capitalizing on a smaller set of labeled image-text pairs and a larger set of unlabeled pairs to achieve competitive performance. Unlike visual segmentation tasks, PNG involves one pixel belonging to multiple open-ended nouns. As a result, existing multi-class based semi-supervised segmentation frameworks cannot be directly applied to this task. To address this challenge, we first develop a novel SS-PNG Network (SS-PNG-NW) tailored to the SS-PNG setting. We thoroughly investigate strategies such as Burn-In and data augmentation to determine the optimal generic configuration for the SS-PNG-NW. Additionally, to tackle the issue of imbalanced pseudo-label quality, we propose a Quality-Based Loss Adjustment (QLA) approach to adjust the semi-supervised objective, resulting in an enhanced SS-PNG-NW+. Employing our proposed QLA, we improve BCE Loss and Dice loss at pixel and mask levels, respectively. We conduct extensive experiments on PNG datasets, with our SS-PNG-NW+ demonstrating promising results comparable to fully-supervised models across all data ratios. Remarkably, our SS-PNG-NW+ outperforms fully-supervised models with only 30% and 50% supervision data, exceeding their performance by 0.8% and 1.1% respectively. This highlights the effectiveness of our proposed SS-PNG-NW+ in overcoming the challenges posed by limited annotations and enhancing the applicability of PNG tasks. The source code is available at https://github.com/nini0919/SSPNG.

Efficient Active Learning Halfspaces with Tsybakov Noise: A Non-convex Optimization Approach

We study the problem of computationally and label efficient PAC active learning $d$-dimensional halfspaces with Tsybakov Noise~\citep{tsybakov2004optimal} under structured unlabeled data distributions. Inspired by~\cite{diakonikolas2020learning}, we prove that any approximate first-order stationary point of a smooth nonconvex loss function yields a halfspace with a low excess error guarantee. In light of the above structural result, we design a nonconvex optimization-based algorithm with a label complexity of $\tilde{O}(d (\frac{1}{\epsilon})^{\frac{8-6\alpha}{3\alpha-1}})$\footnote{In the main body of this work, we use $\tilde{O}(\cdot), \tilde{\Theta}(\cdot)$ to hide factors of the form $\polylog(d, \frac{1}{\epsilon}, \frac{1}{\delta})$}, under the assumption that the Tsybakov noise parameter $\alpha \in (\frac13, 1]$, which narrows down the gap between the label complexities of the previously known efficient passive or active algorithms~\citep{diakonikolas2020polynomial,zhang2021improved} and the information-theoretic lower bound in this setting.

Provable Advantage of Parameterized Quantum Circuit in Function Approximation

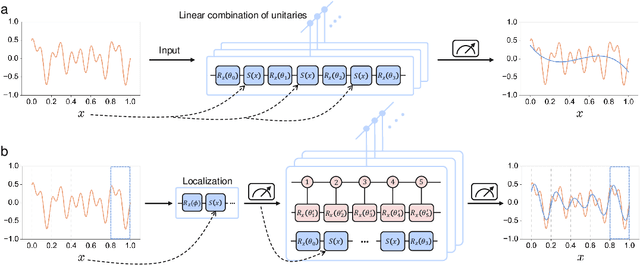
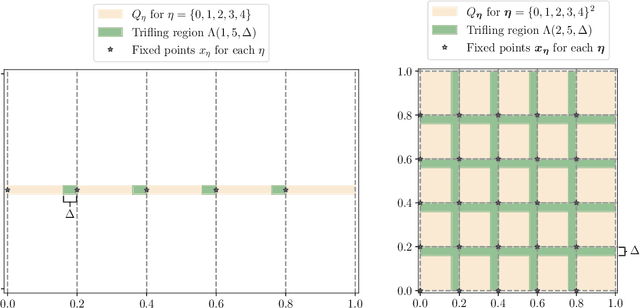
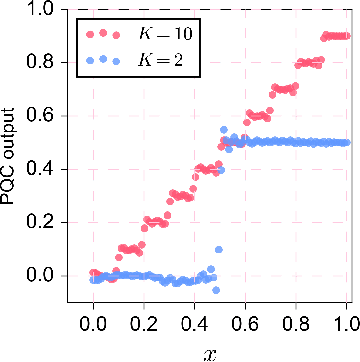
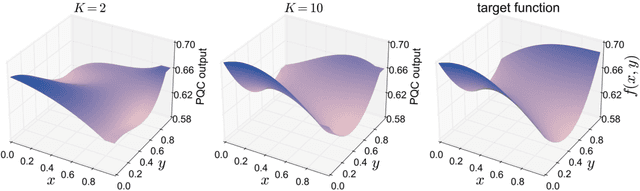
Understanding the power of parameterized quantum circuits (PQCs) in accomplishing machine learning tasks is one of the most important questions in quantum machine learning. In this paper, we analyze the expressivity of PQCs through the lens of function approximation. Previously established universal approximation theorems for PQCs are mainly nonconstructive, leading us to the following question: How large do the PQCs need to be to approximate the target function up to a given error? We exhibit explicit constructions of data re-uploading PQCs for approximating continuous and smooth functions and establish quantitative approximation error bounds in terms of the width, the depth and the number of trainable parameters of the PQCs. To achieve this, we utilize techniques from quantum signal processing and linear combinations of unitaries to construct PQCs that implement multivariate polynomials. We implement global and local approximation techniques using Bernstein polynomials and local Taylor expansion and analyze their performances in the quantum setting. We also compare our proposed PQCs to nearly optimal deep neural networks in approximating high-dimensional smooth functions, showing that the ratio between model sizes of PQC and deep neural networks is exponentially small with respect to the input dimension. This suggests a potentially novel avenue for showcasing quantum advantages in quantum machine learning.

Noise-Augmented $\ell_0$ Regularization of Tensor Regression with Tucker Decomposition

Tensor data are multi-dimension arrays. Low-rank decomposition-based regression methods with tensor predictors exploit the structural information in tensor predictors while significantly reducing the number of parameters in tensor regression. We propose a method named NA$_0$CT$^2$ (Noise Augmentation for $\ell_0$ regularization on Core Tensor in Tucker decomposition) to regularize the parameters in tensor regression (TR), coupled with Tucker decomposition. We establish theoretically that NA$_0$CT$^2$ achieves exact $\ell_0$ regularization in linear TR and generalized linear TR on the core tensor from the Tucker decomposition. To our knowledge, NA$_0$CT$^2$ is the first Tucker decomposition-based regularization method in TR to achieve $\ell_0$ in core tensor. NA$_0$CT$^2$ is implemented through an iterative procedure and involves two simple steps in each iteration -- generating noisy data based on the core tensor from the Tucker decomposition of the updated parameter estimate and running a regular GLM on noise-augmented data on vectorized predictors. We demonstrate the implementation of NA$_0$CT$^2$ and its $\ell_0$ regularization effect in both simulation studies and real data applications. The results suggest that NA$_0$CT$^2$ improves predictions compared to other decomposition-based TR approaches, with or without regularization and it also helps to identify important predictors though not designed for that purpose.

Clover: Towards A Unified Video-Language Alignment and Fusion Model

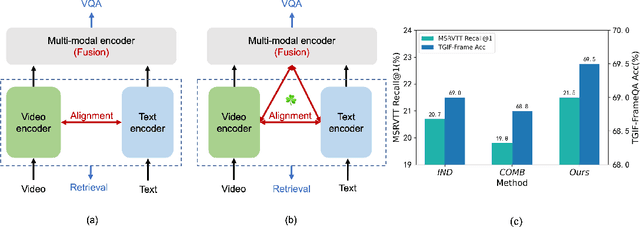
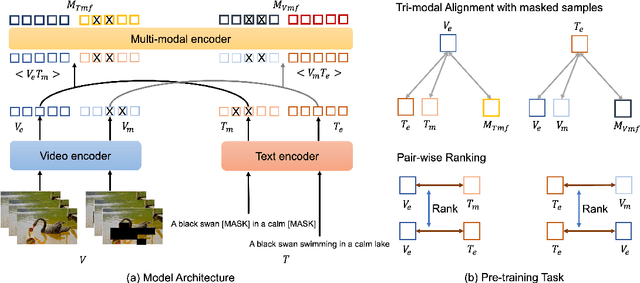
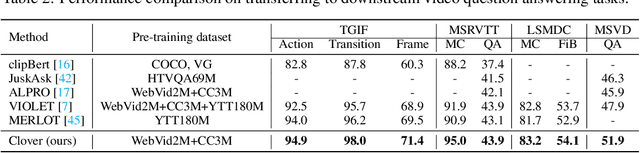
Building a universal video-language model for solving various video understanding tasks (e.g., text-video retrieval, video question answering) is an open challenge to the machine learning field. Towards this goal, most recent attempts train the models, usually consisting of uni-modal and cross-modal feature encoders, with supervised or pair-wise contrastive pre-text tasks. Though offering attractive generality, the resulted models have to compromise between efficiency and performance. We argue the flaws are caused by their pre-training strategies\textemdash they cannot well align and fuse features from different modalities simultaneously. We then introduce Clover -- a Correlated Video-Language pre-training method -- towards a universal video-language model for solving multiple video understanding tasks with neither performance nor efficiency compromise. It improves cross-modal feature alignment and fusion via a novel tri-modal alignment pre-training task. Additionally, we propose to enhance the tri-modal alignment via incorporating learning from masked samples and a novel pair-wise ranking loss. Clover demonstrates outstanding generality. It establishes new state-of-the-arts on multiple downstream tasks, including three retrieval tasks for both zero-shot and fine-tuning settings, and eight video question answering tasks. Codes and pre-trained models will be released at https://github.com/LeeYN-43/Clover.

Adaptive Noisy Data Augmentation for Regularized Estimation and Inference in Generalized Linear Models

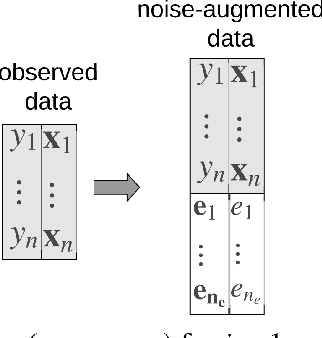
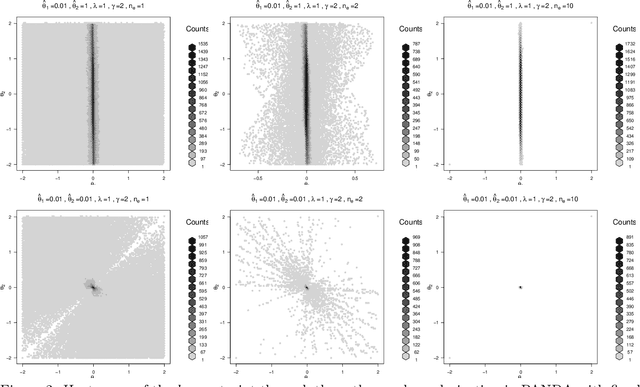
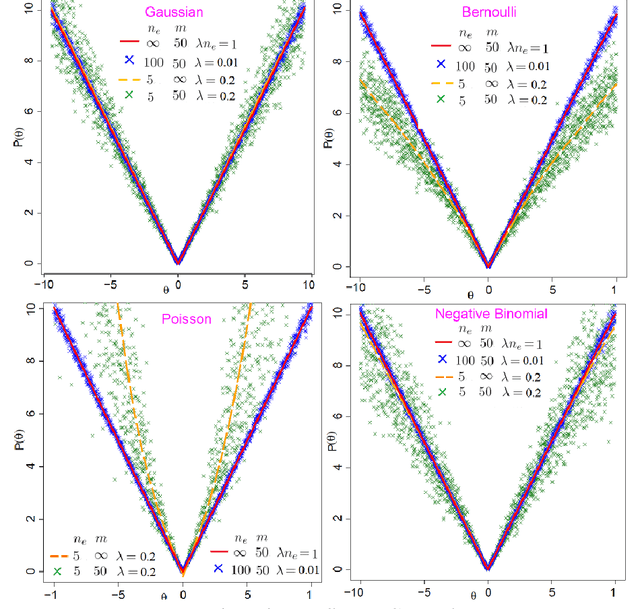
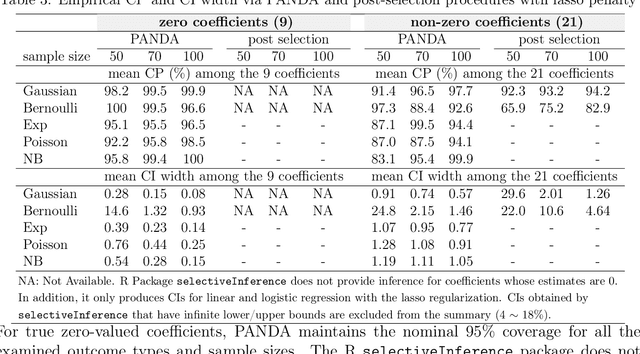
We propose the AdaPtive Noise Augmentation (PANDA) procedure to regularize the estimation and inference of generalized linear models (GLMs). PANDA iteratively optimizes the objective function given noise augmented data until convergence to obtain the regularized model estimates. The augmented noises are designed to achieve various regularization effects, including $l_0$, bridge (lasso and ridge included), elastic net, adaptive lasso, and SCAD, as well as group lasso and fused ridge. We examine the tail bound of the noise-augmented loss function and establish the almost sure convergence of the noise-augmented loss function and its minimizer to the expected penalized loss function and its minimizer, respectively. We derive the asymptotic distributions for the regularized parameters, based on which, inferences can be obtained simultaneously with variable selection. PANDA exhibits ensemble learning behaviors that help further decrease the generalization error. Computationally, PANDA is easy to code, leveraging existing software for implementing GLMs, without resorting to complicated optimization techniques. We demonstrate the superior or similar performance of PANDA against the existing approaches of the same type of regularizers in simulated and real-life data. We show that the inferences through PANDA achieve nominal or near-nominal coverage and are far more efficient compared to a popular existing post-selection procedure.