Unleashing High-Quality Image Generation in Diffusion Sampling Using Second-Order Levenberg-Marquardt-Langevin

The diffusion models (DMs) have demonstrated the remarkable capability of generating images via learning the noised score function of data distribution. Current DM sampling techniques typically rely on first-order Langevin dynamics at each noise level, with efforts concentrated on refining inter-level denoising strategies. While leveraging additional second-order Hessian geometry to enhance the sampling quality of Langevin is a common practice in Markov chain Monte Carlo (MCMC), the naive attempts to utilize Hessian geometry in high-dimensional DMs lead to quadratic-complexity computational costs, rendering them non-scalable. In this work, we introduce a novel Levenberg-Marquardt-Langevin (LML) method that approximates the diffusion Hessian geometry in a training-free manner, drawing inspiration from the celebrated Levenberg-Marquardt optimization algorithm. Our approach introduces two key innovations: (1) A low-rank approximation of the diffusion Hessian, leveraging the DMs' inherent structure and circumventing explicit quadratic-complexity computations; (2) A damping mechanism to stabilize the approximated Hessian. This LML approximated Hessian geometry enables the diffusion sampling to execute more accurate steps and improve the image generation quality. We further conduct a theoretical analysis to substantiate the approximation error bound of low-rank approximation and the convergence property of the damping mechanism. Extensive experiments across multiple pretrained DMs validate that the LML method significantly improves image generation quality, with negligible computational overhead.

Efficiently Access Diffusion Fisher: Within the Outer Product Span Space

Recent Diffusion models (DMs) advancements have explored incorporating the second-order diffusion Fisher information (DF), defined as the negative Hessian of log density, into various downstream tasks and theoretical analysis. However, current practices typically approximate the diffusion Fisher by applying auto-differentiation to the learned score network. This black-box method, though straightforward, lacks any accuracy guarantee and is time-consuming. In this paper, we show that the diffusion Fisher actually resides within a space spanned by the outer products of score and initial data. Based on the outer-product structure, we develop two efficient approximation algorithms to access the trace and matrix-vector multiplication of DF, respectively. These algorithms bypass the auto-differentiation operations with time-efficient vector-product calculations. Furthermore, we establish the approximation error bounds for the proposed algorithms. Experiments in likelihood evaluation and adjoint optimization demonstrate the superior accuracy and reduced computational cost of our proposed algorithms. Additionally, based on the novel outer-product formulation of DF, we design the first numerical verification experiment for the optimal transport property of the general PF-ODE deduced map.

Analyzing and Improving Model Collapse in Rectified Flow Models

Generative models aim to produce synthetic data indistinguishable from real distributions, but iterative training on self-generated data can lead to \emph{model collapse (MC)}, where performance degrades over time. In this work, we provide the first theoretical analysis of MC in Rectified Flow by framing it within the context of Denoising Autoencoders (DAEs). We show that when DAE models are trained on recursively generated synthetic data with small noise variance, they suffer from MC with progressive diminishing generation quality. To address this MC issue, we propose methods that strategically incorporate real data into the training process, even when direct noise-image pairs are unavailable. Our proposed techniques, including Reverse Collapse-Avoiding (RCA) Reflow and Online Collapse-Avoiding Reflow (OCAR), effectively prevent MC while maintaining the efficiency benefits of Rectified Flow. Extensive experiments on standard image datasets demonstrate that our methods not only mitigate MC but also improve sampling efficiency, leading to higher-quality image generation with fewer sampling steps.

BELM: Bidirectional Explicit Linear Multi-step Sampler for Exact Inversion in Diffusion Models

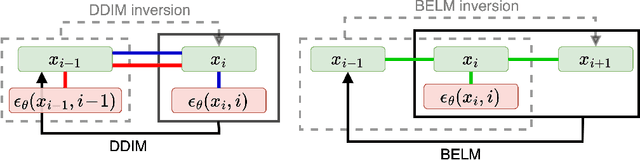
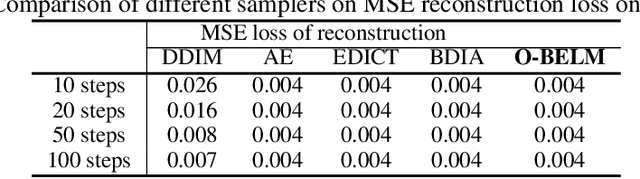
The inversion of diffusion model sampling, which aims to find the corresponding initial noise of a sample, plays a critical role in various tasks. Recently, several heuristic exact inversion samplers have been proposed to address the inexact inversion issue in a training-free manner. However, the theoretical properties of these heuristic samplers remain unknown and they often exhibit mediocre sampling quality. In this paper, we introduce a generic formulation, \emph{Bidirectional Explicit Linear Multi-step} (BELM) samplers, of the exact inversion samplers, which includes all previously proposed heuristic exact inversion samplers as special cases. The BELM formulation is derived from the variable-stepsize-variable-formula linear multi-step method via integrating a bidirectional explicit constraint. We highlight this bidirectional explicit constraint is the key of mathematically exact inversion. We systematically investigate the Local Truncation Error (LTE) within the BELM framework and show that the existing heuristic designs of exact inversion samplers yield sub-optimal LTE. Consequently, we propose the Optimal BELM (O-BELM) sampler through the LTE minimization approach. We conduct additional analysis to substantiate the theoretical stability and global convergence property of the proposed optimal sampler. Comprehensive experiments demonstrate our O-BELM sampler establishes the exact inversion property while achieving high-quality sampling. Additional experiments in image editing and image interpolation highlight the extensive potential of applying O-BELM in varying applications.

Neural Sinkhorn Gradient Flow

Wasserstein Gradient Flows (WGF) with respect to specific functionals have been widely used in the machine learning literature. Recently, neural networks have been adopted to approximate certain intractable parts of the underlying Wasserstein gradient flow and result in efficient inference procedures. In this paper, we introduce the Neural Sinkhorn Gradient Flow (NSGF) model, which parametrizes the time-varying velocity field of the Wasserstein gradient flow w.r.t. the Sinkhorn divergence to the target distribution starting a given source distribution. We utilize the velocity field matching training scheme in NSGF, which only requires samples from the source and target distribution to compute an empirical velocity field approximation. Our theoretical analyses show that as the sample size increases to infinity, the mean-field limit of the empirical approximation converges to the true underlying velocity field. To further enhance model efficiency on high-dimensional tasks, a two-phase NSGF++ model is devised, which first follows the Sinkhorn flow to approach the image manifold quickly ($\le 5$ NFEs) and then refines the samples along a simple straight flow. Numerical experiments with synthetic and real-world benchmark datasets support our theoretical results and demonstrate the effectiveness of the proposed methods.

GAD-PVI: A General Accelerated Dynamic-Weight Particle-Based Variational Inference Framework

Particle-based Variational Inference (ParVI) methods approximate the target distribution by iteratively evolving finite weighted particle systems. Recent advances of ParVI methods reveal the benefits of accelerated position update strategies and dynamic weight adjustment approaches. In this paper, we propose the first ParVI framework that possesses both accelerated position update and dynamical weight adjustment simultaneously, named the General Accelerated Dynamic-Weight Particle-based Variational Inference (GAD-PVI) framework. Generally, GAD-PVI simulates the semi-Hamiltonian gradient flow on a novel Information-Fisher-Rao space, which yields an additional decrease on the local functional dissipation. GAD-PVI is compatible with different dissimilarity functionals and associated smoothing approaches under three information metrics. Experiments on both synthetic and real-world data demonstrate the faster convergence and reduced approximation error of GAD-PVI methods over the state-of-the-art.