Rethinking the Flow-Based Gradual Domain Adaption: A Semi-Dual Optimal Transport Perspective

Gradual domain adaptation (GDA) aims to mitigate domain shift by progressively adapting models from the source domain to the target domain via intermediate domains. However, real intermediate domains are often unavailable or ineffective, necessitating the synthesis of intermediate samples. Flow-based models have recently been used for this purpose by interpolating between source and target distributions; however, their training typically relies on sample-based log-likelihood estimation, which can discard useful information and thus degrade GDA performance. The key to addressing this limitation is constructing the intermediate domains via samples directly. To this end, we propose an Entropy-regularized Semi-dual Unbalanced Optimal Transport (E-SUOT) framework to construct intermediate domains. Specifically, we reformulate flow-based GDA as a Lagrangian dual problem and derive an equivalent semi-dual objective that circumvents the need for likelihood estimation. However, the dual problem leads to an unstable min-max training procedure. To alleviate this issue, we further introduce entropy regularization to convert it into a more stable alternative optimization procedure. Based on this, we propose a novel GDA training framework and provide theoretical analysis in terms of stability and generalization. Finally, extensive experiments are conducted to demonstrate the efficacy of the E-SUOT framework.

Analyzing and Improving Diffusion Models for Time-Series Data Imputation: A Proximal Recursion Perspective

Diffusion models (DMs) have shown promise for Time-Series Data Imputation (TSDI); however, their performance remains inconsistent in complex scenarios. We attribute this to two primary obstacles: (1) non-stationary temporal dynamics, which can bias the inference trajectory and lead to outlier-sensitive imputations; and (2) objective inconsistency, since imputation favors accurate pointwise recovery whereas DMs are inherently trained to generate diverse samples. To better understand these issues, we analyze DM-based TSDI process through a proximal-operator perspective and uncover that an implicit Wasserstein distance regularization inherent in the process hinders the model's ability to counteract non-stationarity and dissipative regularizer, thereby amplifying diversity at the expense of fidelity. Building on this insight, we propose a novel framework called SPIRIT (Semi-Proximal Transport Regularized time-series Imputation). Specifically, we introduce entropy-induced Bregman divergence to relax the mass preserving constraint in the Wasserstein distance, formulate the semi-proximal transport (SPT) discrepancy, and theoretically prove the robustness of SPT against non-stationarity. Subsequently, we remove the dissipative structure and derive the complete SPIRIT workflow, with SPT serving as the proximal operator. Extensive experiments demonstrate the effectiveness of the proposed SPIRIT approach.

Unleashing High-Quality Image Generation in Diffusion Sampling Using Second-Order Levenberg-Marquardt-Langevin

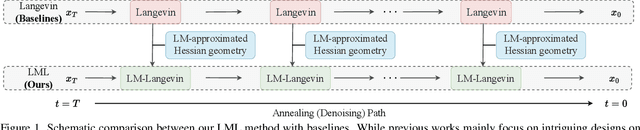
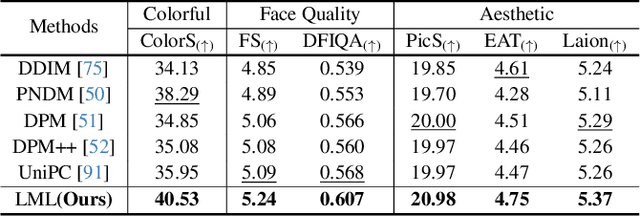
The diffusion models (DMs) have demonstrated the remarkable capability of generating images via learning the noised score function of data distribution. Current DM sampling techniques typically rely on first-order Langevin dynamics at each noise level, with efforts concentrated on refining inter-level denoising strategies. While leveraging additional second-order Hessian geometry to enhance the sampling quality of Langevin is a common practice in Markov chain Monte Carlo (MCMC), the naive attempts to utilize Hessian geometry in high-dimensional DMs lead to quadratic-complexity computational costs, rendering them non-scalable. In this work, we introduce a novel Levenberg-Marquardt-Langevin (LML) method that approximates the diffusion Hessian geometry in a training-free manner, drawing inspiration from the celebrated Levenberg-Marquardt optimization algorithm. Our approach introduces two key innovations: (1) A low-rank approximation of the diffusion Hessian, leveraging the DMs' inherent structure and circumventing explicit quadratic-complexity computations; (2) A damping mechanism to stabilize the approximated Hessian. This LML approximated Hessian geometry enables the diffusion sampling to execute more accurate steps and improve the image generation quality. We further conduct a theoretical analysis to substantiate the approximation error bound of low-rank approximation and the convergence property of the damping mechanism. Extensive experiments across multiple pretrained DMs validate that the LML method significantly improves image generation quality, with negligible computational overhead.

Efficiently Access Diffusion Fisher: Within the Outer Product Span Space

Recent Diffusion models (DMs) advancements have explored incorporating the second-order diffusion Fisher information (DF), defined as the negative Hessian of log density, into various downstream tasks and theoretical analysis. However, current practices typically approximate the diffusion Fisher by applying auto-differentiation to the learned score network. This black-box method, though straightforward, lacks any accuracy guarantee and is time-consuming. In this paper, we show that the diffusion Fisher actually resides within a space spanned by the outer products of score and initial data. Based on the outer-product structure, we develop two efficient approximation algorithms to access the trace and matrix-vector multiplication of DF, respectively. These algorithms bypass the auto-differentiation operations with time-efficient vector-product calculations. Furthermore, we establish the approximation error bounds for the proposed algorithms. Experiments in likelihood evaluation and adjoint optimization demonstrate the superior accuracy and reduced computational cost of our proposed algorithms. Additionally, based on the novel outer-product formulation of DF, we design the first numerical verification experiment for the optimal transport property of the general PF-ODE deduced map.

Video-GPT via Next Clip Diffusion

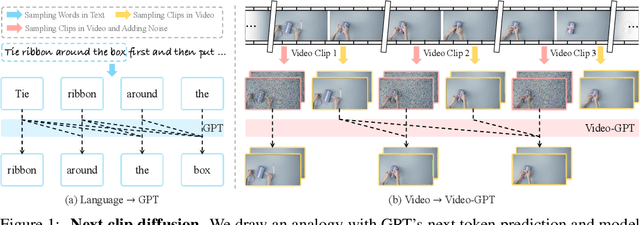
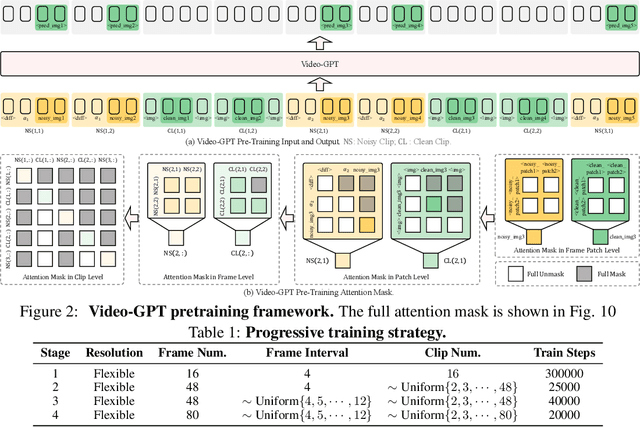
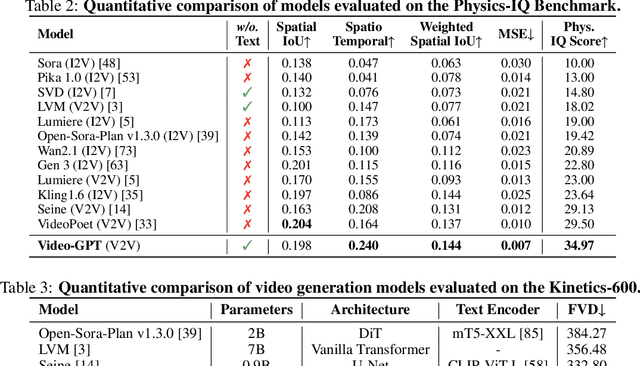
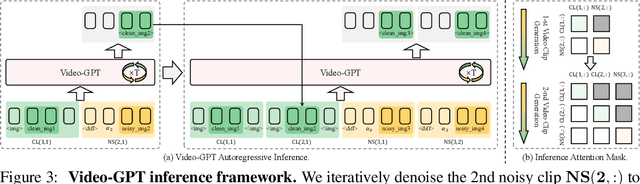
GPT has shown its remarkable success in natural language processing. However, the language sequence is not sufficient to describe spatial-temporal details in the visual world. Alternatively, the video sequence is good at capturing such details. Motivated by this fact, we propose a concise Video-GPT in this paper by treating video as new language for visual world modeling. By analogy to next token prediction in GPT, we introduce a novel next clip diffusion paradigm for pretraining Video-GPT. Different from the previous works, this distinct paradigm allows Video-GPT to tackle both short-term generation and long-term prediction, by autoregressively denoising the noisy clip according to the clean clips in the history. Extensive experiments show our Video-GPT achieves the state-of-the-art performance on video prediction, which is the key factor towards world modeling (Physics-IQ Benchmark: Video-GPT 34.97 vs. Kling 23.64 vs. Wan 20.89). Moreover, it can be well adapted on 6 mainstream video tasks in both video generation and understanding, showing its great generalization capacity in downstream. The project page is at https://Video-GPT.github.io.

TimeStep Master: Asymmetrical Mixture of Timestep LoRA Experts for Versatile and Efficient Diffusion Models in Vision

Diffusion models have driven the advancement of vision generation over the past years. However, it is often difficult to apply these large models in downstream tasks, due to massive fine-tuning cost. Recently, Low-Rank Adaptation (LoRA) has been applied for efficient tuning of diffusion models. Unfortunately, the capabilities of LoRA-tuned diffusion models are limited, since the same LoRA is used for different timesteps of the diffusion process. To tackle this problem, we introduce a general and concise TimeStep Master (TSM) paradigm with two key fine-tuning stages. In the fostering stage (1-stage), we apply different LoRAs to fine-tune the diffusion model at different timestep intervals. This results in different TimeStep LoRA experts that can effectively capture different noise levels. In the assembling stage (2-stage), we design a novel asymmetrical mixture of TimeStep LoRA experts, via core-context collaboration of experts at multi-scale intervals. For each timestep, we leverage TimeStep LoRA expert within the smallest interval as the core expert without gating, and use experts within the bigger intervals as the context experts with time-dependent gating. Consequently, our TSM can effectively model the noise level via the expert in the finest interval, and adaptively integrate contexts from the experts of other scales, boosting the versatility of diffusion models. To show the effectiveness of our TSM paradigm, we conduct extensive experiments on three typical and popular LoRA-related tasks of diffusion models, including domain adaptation, post-pretraining, and model distillation. Our TSM achieves the state-of-the-art results on all these tasks, throughout various model structures (UNet, DiT and MM-DiT) and visual data modalities (Image, Video), showing its remarkable generalization capacity.

Get In Video: Add Anything You Want to the Video

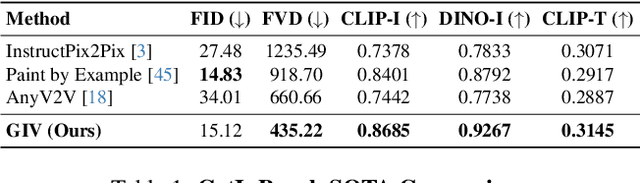
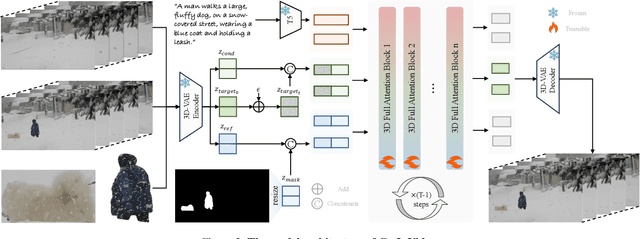
Video editing increasingly demands the ability to incorporate specific real-world instances into existing footage, yet current approaches fundamentally fail to capture the unique visual characteristics of particular subjects and ensure natural instance/scene interactions. We formalize this overlooked yet critical editing paradigm as "Get-In-Video Editing", where users provide reference images to precisely specify visual elements they wish to incorporate into videos. Addressing this task's dual challenges, severe training data scarcity and technical challenges in maintaining spatiotemporal coherence, we introduce three key contributions. First, we develop GetIn-1M dataset created through our automated Recognize-Track-Erase pipeline, which sequentially performs video captioning, salient instance identification, object detection, temporal tracking, and instance removal to generate high-quality video editing pairs with comprehensive annotations (reference image, tracking mask, instance prompt). Second, we present GetInVideo, a novel end-to-end framework that leverages a diffusion transformer architecture with 3D full attention to process reference images, condition videos, and masks simultaneously, maintaining temporal coherence, preserving visual identity, and ensuring natural scene interactions when integrating reference objects into videos. Finally, we establish GetInBench, the first comprehensive benchmark for Get-In-Video Editing scenario, demonstrating our approach's superior performance through extensive evaluations. Our work enables accessible, high-quality incorporation of specific real-world subjects into videos, significantly advancing personalized video editing capabilities.

Analyzing and Improving Model Collapse in Rectified Flow Models

Generative models aim to produce synthetic data indistinguishable from real distributions, but iterative training on self-generated data can lead to \emph{model collapse (MC)}, where performance degrades over time. In this work, we provide the first theoretical analysis of MC in Rectified Flow by framing it within the context of Denoising Autoencoders (DAEs). We show that when DAE models are trained on recursively generated synthetic data with small noise variance, they suffer from MC with progressive diminishing generation quality. To address this MC issue, we propose methods that strategically incorporate real data into the training process, even when direct noise-image pairs are unavailable. Our proposed techniques, including Reverse Collapse-Avoiding (RCA) Reflow and Online Collapse-Avoiding Reflow (OCAR), effectively prevent MC while maintaining the efficiency benefits of Rectified Flow. Extensive experiments on standard image datasets demonstrate that our methods not only mitigate MC but also improve sampling efficiency, leading to higher-quality image generation with fewer sampling steps.

BELM: Bidirectional Explicit Linear Multi-step Sampler for Exact Inversion in Diffusion Models

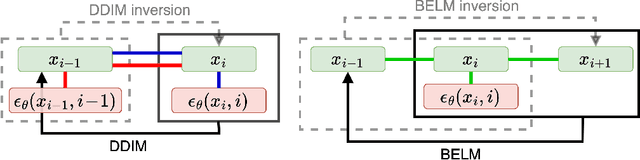
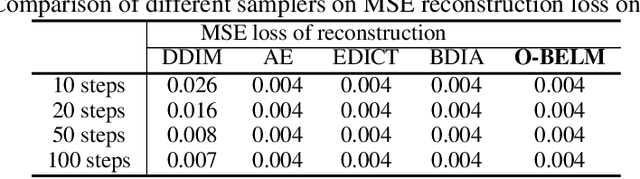
The inversion of diffusion model sampling, which aims to find the corresponding initial noise of a sample, plays a critical role in various tasks. Recently, several heuristic exact inversion samplers have been proposed to address the inexact inversion issue in a training-free manner. However, the theoretical properties of these heuristic samplers remain unknown and they often exhibit mediocre sampling quality. In this paper, we introduce a generic formulation, \emph{Bidirectional Explicit Linear Multi-step} (BELM) samplers, of the exact inversion samplers, which includes all previously proposed heuristic exact inversion samplers as special cases. The BELM formulation is derived from the variable-stepsize-variable-formula linear multi-step method via integrating a bidirectional explicit constraint. We highlight this bidirectional explicit constraint is the key of mathematically exact inversion. We systematically investigate the Local Truncation Error (LTE) within the BELM framework and show that the existing heuristic designs of exact inversion samplers yield sub-optimal LTE. Consequently, we propose the Optimal BELM (O-BELM) sampler through the LTE minimization approach. We conduct additional analysis to substantiate the theoretical stability and global convergence property of the proposed optimal sampler. Comprehensive experiments demonstrate our O-BELM sampler establishes the exact inversion property while achieving high-quality sampling. Additional experiments in image editing and image interpolation highlight the extensive potential of applying O-BELM in varying applications.

Rethinking the Diffusion Models for Numerical Tabular Data Imputation from the Perspective of Wasserstein Gradient Flow

Diffusion models (DMs) have gained attention in Missing Data Imputation (MDI), but there remain two long-neglected issues to be addressed: (1). Inaccurate Imputation, which arises from inherently sample-diversification-pursuing generative process of DMs. (2). Difficult Training, which stems from intricate design required for the mask matrix in model training stage. To address these concerns within the realm of numerical tabular datasets, we introduce a novel principled approach termed Kernelized Negative Entropy-regularized Wasserstein gradient flow Imputation (KnewImp). Specifically, based on Wasserstein gradient flow (WGF) framework, we first prove that issue (1) stems from the cost functionals implicitly maximized in DM-based MDI are equivalent to the MDI's objective plus diversification-promoting non-negative terms. Based on this, we then design a novel cost functional with diversification-discouraging negative entropy and derive our KnewImp approach within WGF framework and reproducing kernel Hilbert space. After that, we prove that the imputation procedure of KnewImp can be derived from another cost functional related to the joint distribution, eliminating the need for the mask matrix and hence naturally addressing issue (2). Extensive experiments demonstrate that our proposed KnewImp approach significantly outperforms existing state-of-the-art methods.