Mathematical Reasoning for Unmanned Aerial Vehicles: A RAG-Based Approach for Complex Arithmetic Reasoning

Autonomous UAV operation necessitates reliable mathematical reasoning for tasks such as trajectory planning and power management. While traditional flight control relies on hardcoded equations, recent Large Language Models (LLMs) offer potential for more flexible problem-solving but struggle with reliably selecting and applying correct mathematical formulations and executing precise multi-step arithmetic. We propose RAG-UAV, a retrieval-augmented generation framework designed to improve the mathematical reasoning of several LLMs (including GPT o1/Turbo, Llama-3.2/3.3, Mistral, and DeepSeek R1) in UAV-specific contexts by providing access to relevant domain literature. To conduct an initial assessment, we introduce the UAV-Math-Bench, a small problem set comprising 20 UAV-centric mathematical problems across four difficulty levels. Our experiments demonstrate that incorporating retrieval substantially increases exact answer accuracy (achieving up to 75% with o1), reduces instances of incorrect formulation selection (from 25% without RAG to 5% with RAG), decreases numerical errors, reducing Mean Squared Error (MSE) by orders of magnitude for the best-performing models. This pilot study indicates that RAG can enable general-purpose LLMs to function as more reliable tools for engineering analysis, although direct real-time flight control requires further investigation and validation on a larger scale. All benchmark data, question and answer are publicly available.

Towards Foundation Model on Temporal Knowledge Graph Reasoning

Temporal Knowledge Graphs (TKGs) store temporal facts with quadruple formats (s, p, o, t). Existing Temporal Knowledge Graph Embedding (TKGE) models perform link prediction tasks in transductive or semi-inductive settings, which means the entities, relations, and temporal information in the test graph are fully or partially observed during training. Such reliance on seen elements during inference limits the models' ability to transfer to new domains and generalize to real-world scenarios. A central limitation is the difficulty in learning representations for entities, relations, and timestamps that are transferable and not tied to dataset-specific vocabularies. To overcome these limitations, we introduce the first fully-inductive approach to temporal knowledge graph link prediction. Our model employs sinusoidal positional encodings to capture fine-grained temporal patterns and generates adaptive entity and relation representations using message passing conditioned on both local and global temporal contexts. Our model design is agnostic to temporal granularity and time span, effectively addressing temporal discrepancies across TKGs and facilitating time-aware structural information transfer. As a pretrained, scalable, and transferable model, POSTRA demonstrates strong zero-shot performance on unseen temporal knowledge graphs, effectively generalizing to novel entities, relations, and timestamps. Extensive theoretical analysis and empirical results show that a single pretrained model can improve zero-shot performance on various inductive temporal reasoning scenarios, marking a significant step toward a foundation model for temporal KGs.

SEMMA: A Semantic Aware Knowledge Graph Foundation Model

Knowledge Graph Foundation Models (KGFMs) have shown promise in enabling zero-shot reasoning over unseen graphs by learning transferable patterns. However, most existing KGFMs rely solely on graph structure, overlooking the rich semantic signals encoded in textual attributes. We introduce SEMMA, a dual-module KGFM that systematically integrates transferable textual semantics alongside structure. SEMMA leverages Large Language Models (LLMs) to enrich relation identifiers, generating semantic embeddings that subsequently form a textual relation graph, which is fused with the structural component. Across 54 diverse KGs, SEMMA outperforms purely structural baselines like ULTRA in fully inductive link prediction. Crucially, we show that in more challenging generalization settings, where the test-time relation vocabulary is entirely unseen, structural methods collapse while SEMMA is 2x more effective. Our findings demonstrate that textual semantics are critical for generalization in settings where structure alone fails, highlighting the need for foundation models that unify structural and linguistic signals in knowledge reasoning.

Predictive Multiplicity of Knowledge Graph Embeddings in Link Prediction

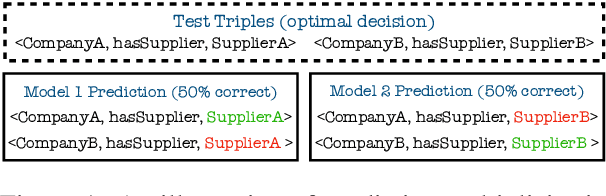
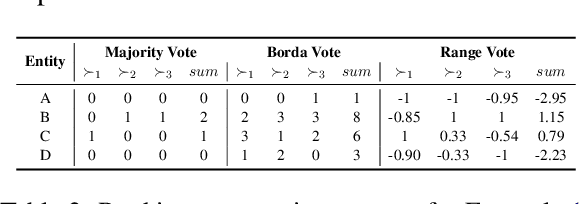
Knowledge graph embedding (KGE) models are often used to predict missing links for knowledge graphs (KGs). However, multiple KG embeddings can perform almost equally well for link prediction yet suggest conflicting predictions for certain queries, termed \textit{predictive multiplicity} in literature. This behavior poses substantial risks for KGE-based applications in high-stake domains but has been overlooked in KGE research. In this paper, we define predictive multiplicity in link prediction. We introduce evaluation metrics and measure predictive multiplicity for representative KGE methods on commonly used benchmark datasets. Our empirical study reveals significant predictive multiplicity in link prediction, with $8\%$ to $39\%$ testing queries exhibiting conflicting predictions. To address this issue, we propose leveraging voting methods from social choice theory, significantly mitigating conflicts by $66\%$ to $78\%$ according to our experiments.

Approximating Probabilistic Inference in Statistical EL with Knowledge Graph Embeddings

Statistical information is ubiquitous but drawing valid conclusions from it is prohibitively hard. We explain how knowledge graph embeddings can be used to approximate probabilistic inference efficiently using the example of Statistical EL (SEL), a statistical extension of the lightweight Description Logic EL. We provide proofs for runtime and soundness guarantees, and empirically evaluate the runtime and approximation quality of our approach.

Generating SROI^{-} Ontologies via Knowledge Graph Query Embedding Learning

Query embedding approaches answer complex logical queries over incomplete knowledge graphs (KGs) by computing and operating on low-dimensional vector representations of entities, relations, and queries. However, current query embedding models heavily rely on excessively parameterized neural networks and cannot explain the knowledge learned from the graph. We propose a novel query embedding method, AConE, which explains the knowledge learned from the graph in the form of SROI^{-} description logic axioms while being more parameter-efficient than most existing approaches. AConE associates queries to a SROI^{-} description logic concept. Every SROI^{-} concept is embedded as a cone in complex vector space, and each SROI^{-} relation is embedded as a transformation that rotates and scales cones. We show theoretically that AConE can learn SROI^{-} axioms, and defines an algebra whose operations correspond one to one to SROI^{-} description logic concept constructs. Our empirical study on multiple query datasets shows that AConE achieves superior results over previous baselines with fewer parameters. Notably on the WN18RR dataset, AConE achieves significant improvement over baseline models. We provide comprehensive analyses showing that the capability to represent axioms positively impacts the results of query answering.

Hybrid Reasoning Based on Large Language Models for Autonomous Car Driving

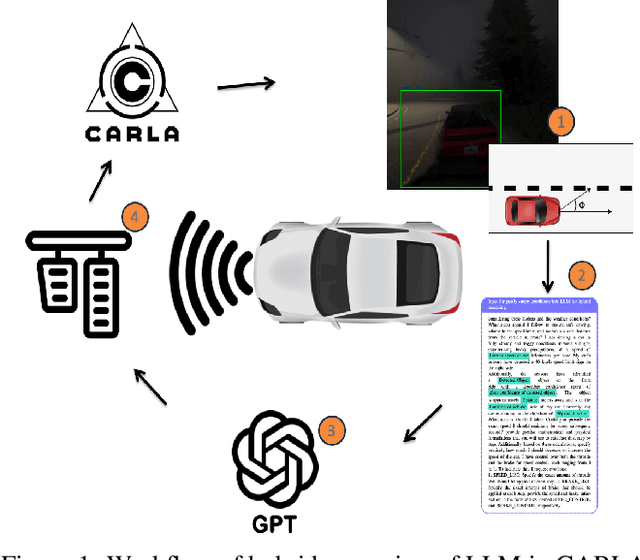
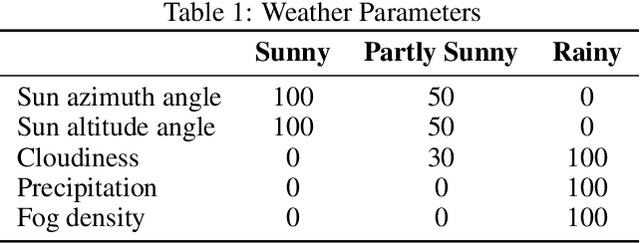
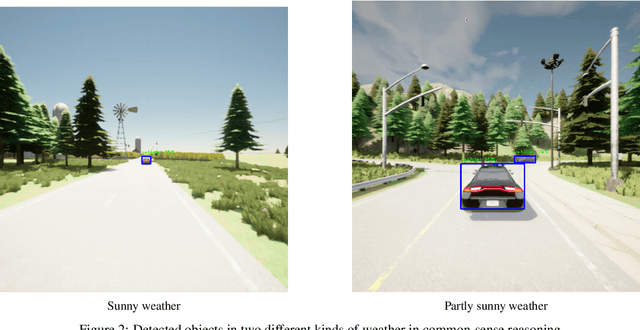
Large Language Models (LLMs) have garnered significant attention for their ability to understand text and images, generate human-like text, and perform complex reasoning tasks. However, their ability to generalize this advanced reasoning with a combination of natural language text for decision-making in dynamic situations requires further exploration. In this study, we investigate how well LLMs can adapt and apply a combination of arithmetic and common-sense reasoning, particularly in autonomous driving scenarios. We hypothesize that LLMs hybrid reasoning abilities can improve autonomous driving by enabling them to analyze detected object and sensor data, understand driving regulations and physical laws, and offer additional context. This addresses complex scenarios, like decisions in low visibility (due to weather conditions), where traditional methods might fall short. We evaluated Large Language Models (LLMs) based on accuracy by comparing their answers with human-generated ground truth inside CARLA. The results showed that when a combination of images (detected objects) and sensor data is fed into the LLM, it can offer precise information for brake and throttle control in autonomous vehicles across various weather conditions. This formulation and answers can assist in decision-making for auto-pilot systems.

HGE: Embedding Temporal Knowledge Graphs in a Product Space of Heterogeneous Geometric Subspaces

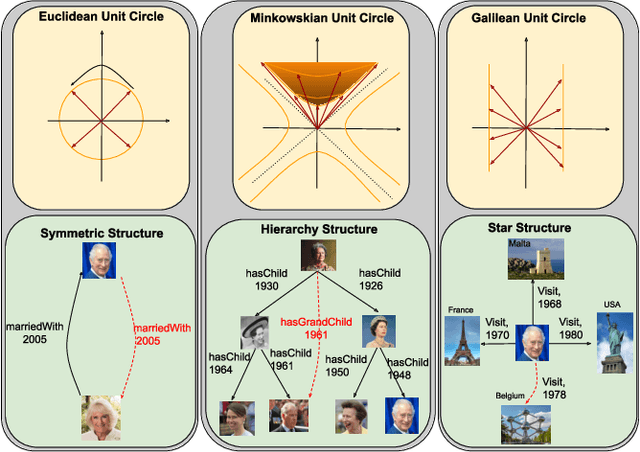
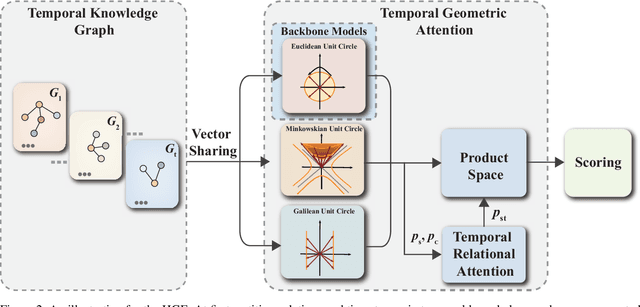
Temporal knowledge graphs represent temporal facts $(s,p,o,\tau)$ relating a subject $s$ and an object $o$ via a relation label $p$ at time $\tau$, where $\tau$ could be a time point or time interval. Temporal knowledge graphs may exhibit static temporal patterns at distinct points in time and dynamic temporal patterns between different timestamps. In order to learn a rich set of static and dynamic temporal patterns and apply them for inference, several embedding approaches have been suggested in the literature. However, as most of them resort to single underlying embedding spaces, their capability to model all kinds of temporal patterns was severely limited by having to adhere to the geometric property of their one embedding space. We lift this limitation by an embedding approach that maps temporal facts into a product space of several heterogeneous geometric subspaces with distinct geometric properties, i.e.\ Complex, Dual, and Split-complex spaces. In addition, we propose a temporal-geometric attention mechanism to integrate information from different geometric subspaces conveniently according to the captured relational and temporal information. Experimental results on standard temporal benchmark datasets favorably evaluate our approach against state-of-the-art models.

NestE: Modeling Nested Relational Structures for Knowledge Graph Reasoning

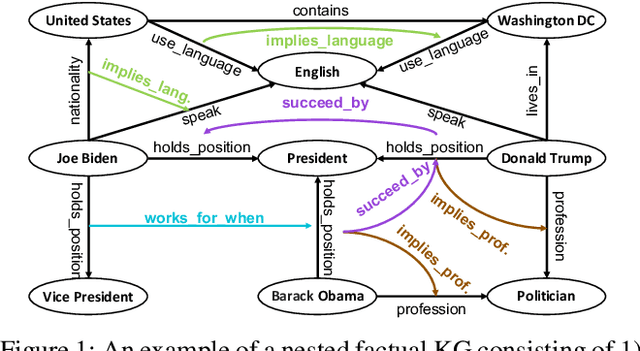
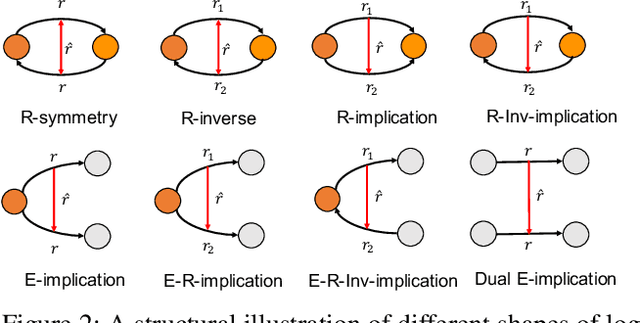
Reasoning with knowledge graphs (KGs) has primarily focused on triple-shaped facts. Recent advancements have been explored to enhance the semantics of these facts by incorporating more potent representations, such as hyper-relational facts. However, these approaches are limited to \emph{atomic facts}, which describe a single piece of information. This paper extends beyond \emph{atomic facts} and delves into \emph{nested facts}, represented by quoted triples where subjects and objects are triples themselves (e.g., ((\emph{BarackObama}, \emph{holds\_position}, \emph{President}), \emph{succeed\_by}, (\emph{DonaldTrump}, \emph{holds\_position}, \emph{President}))). These nested facts enable the expression of complex semantics like \emph{situations} over time and \emph{logical patterns} over entities and relations. In response, we introduce NestE, a novel KG embedding approach that captures the semantics of both atomic and nested factual knowledge. NestE represents each atomic fact as a $1\times3$ matrix, and each nested relation is modeled as a $3\times3$ matrix that rotates the $1\times3$ atomic fact matrix through matrix multiplication. Each element of the matrix is represented as a complex number in the generalized 4D hypercomplex space, including (spherical) quaternions, hyperbolic quaternions, and split-quaternions. Through thorough analysis, we demonstrate the embedding's efficacy in capturing diverse logical patterns over nested facts, surpassing the confines of first-order logic-like expressions. Our experimental results showcase NestE's significant performance gains over current baselines in triple prediction and conditional link prediction. The code and pre-trained models are open available at https://github.com/xiongbo010/NestE.

Geometric Relational Embeddings: A Survey

Geometric relational embeddings map relational data as geometric objects that combine vector information suitable for machine learning and structured/relational information for structured/relational reasoning, typically in low dimensions. Their preservation of relational structures and their appealing properties and interpretability have led to their uptake for tasks such as knowledge graph completion, ontology and hierarchy reasoning, logical query answering, and hierarchical multi-label classification. We survey methods that underly geometric relational embeddings and categorize them based on (i) the embedding geometries that are used to represent the data; and (ii) the relational reasoning tasks that they aim to improve. We identify the desired properties (i.e., inductive biases) of each kind of embedding and discuss some potential future work.