Yunjie He
DAGE: DAG Query Answering via Relational Combinator with Logical Constraints
Oct 29, 2024Abstract:Predicting answers to queries over knowledge graphs is called a complex reasoning task because answering a query requires subdividing it into subqueries. Existing query embedding methods use this decomposition to compute the embedding of a query as the combination of the embedding of the subqueries. This requirement limits the answerable queries to queries having a single free variable and being decomposable, which are called tree-form queries and correspond to the $\mathcal{SROI}^-$ description logic. In this paper, we define a more general set of queries, called DAG queries and formulated in the $\mathcal{ALCOIR}$ description logic, propose a query embedding method for them, called DAGE, and a new benchmark to evaluate query embeddings on them. Given the computational graph of a DAG query, DAGE combines the possibly multiple paths between two nodes into a single path with a trainable operator that represents the intersection of relations and learns DAG-DL from tautologies. We show that it is possible to implement DAGE on top of existing query embedding methods, and we empirically measure the improvement of our method over the results of vanilla methods evaluated in tree-form queries that approximate the DAG queries of our proposed benchmark.
Conformalized Answer Set Prediction for Knowledge Graph Embedding
Aug 15, 2024Abstract:Knowledge graph embeddings (KGE) apply machine learning methods on knowledge graphs (KGs) to provide non-classical reasoning capabilities based on similarities and analogies. The learned KG embeddings are typically used to answer queries by ranking all potential answers, but rankings often lack a meaningful probabilistic interpretation - lower-ranked answers do not necessarily have a lower probability of being true. This limitation makes it difficult to distinguish plausible from implausible answers, posing challenges for the application of KGE methods in high-stakes domains like medicine. We address this issue by applying the theory of conformal prediction that allows generating answer sets, which contain the correct answer with probabilistic guarantees. We explain how conformal prediction can be used to generate such answer sets for link prediction tasks. Our empirical evaluation on four benchmark datasets using six representative KGE methods validates that the generated answer sets satisfy the probabilistic guarantees given by the theory of conformal prediction. We also demonstrate that the generated answer sets often have a sensible size and that the size adapts well with respect to the difficulty of the query.
Predictive Multiplicity of Knowledge Graph Embeddings in Link Prediction
Aug 15, 2024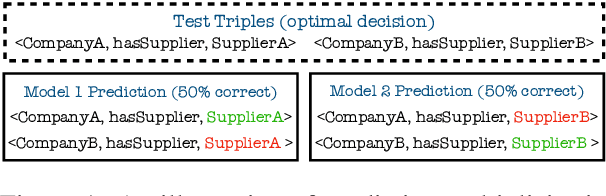

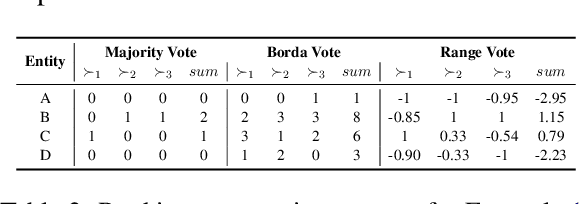

Abstract:Knowledge graph embedding (KGE) models are often used to predict missing links for knowledge graphs (KGs). However, multiple KG embeddings can perform almost equally well for link prediction yet suggest conflicting predictions for certain queries, termed \textit{predictive multiplicity} in literature. This behavior poses substantial risks for KGE-based applications in high-stake domains but has been overlooked in KGE research. In this paper, we define predictive multiplicity in link prediction. We introduce evaluation metrics and measure predictive multiplicity for representative KGE methods on commonly used benchmark datasets. Our empirical study reveals significant predictive multiplicity in link prediction, with $8\%$ to $39\%$ testing queries exhibiting conflicting predictions. To address this issue, we propose leveraging voting methods from social choice theory, significantly mitigating conflicts by $66\%$ to $78\%$ according to our experiments.
Generating SROI^{-} Ontologies via Knowledge Graph Query Embedding Learning
Jul 12, 2024Abstract:Query embedding approaches answer complex logical queries over incomplete knowledge graphs (KGs) by computing and operating on low-dimensional vector representations of entities, relations, and queries. However, current query embedding models heavily rely on excessively parameterized neural networks and cannot explain the knowledge learned from the graph. We propose a novel query embedding method, AConE, which explains the knowledge learned from the graph in the form of SROI^{-} description logic axioms while being more parameter-efficient than most existing approaches. AConE associates queries to a SROI^{-} description logic concept. Every SROI^{-} concept is embedded as a cone in complex vector space, and each SROI^{-} relation is embedded as a transformation that rotates and scales cones. We show theoretically that AConE can learn SROI^{-} axioms, and defines an algebra whose operations correspond one to one to SROI^{-} description logic concept constructs. Our empirical study on multiple query datasets shows that AConE achieves superior results over previous baselines with fewer parameters. Notably on the WN18RR dataset, AConE achieves significant improvement over baseline models. We provide comprehensive analyses showing that the capability to represent axioms positively impacts the results of query answering.
Robust Knowledge Extraction from Large Language Models using Social Choice Theory
Dec 22, 2023Abstract:Large-language models (LLMs) have the potential to support a wide range of applications like conversational agents, creative writing, text improvement, and general query answering. However, they are ill-suited for query answering in high-stake domains like medicine because they generate answers at random and their answers are typically not robust - even the same query can result in different answers when prompted multiple times. In order to improve the robustness of LLM queries, we propose using ranking queries repeatedly and to aggregate the queries using methods from social choice theory. We study ranking queries in diagnostic settings like medical and fault diagnosis and discuss how the Partial Borda Choice function from the literature can be applied to merge multiple query results. We discuss some additional interesting properties in our setting and evaluate the robustness of our approach empirically.
Geometric Relational Embeddings: A Survey
Apr 24, 2023Abstract:Geometric relational embeddings map relational data as geometric objects that combine vector information suitable for machine learning and structured/relational information for structured/relational reasoning, typically in low dimensions. Their preservation of relational structures and their appealing properties and interpretability have led to their uptake for tasks such as knowledge graph completion, ontology and hierarchy reasoning, logical query answering, and hierarchical multi-label classification. We survey methods that underly geometric relational embeddings and categorize them based on (i) the embedding geometries that are used to represent the data; and (ii) the relational reasoning tasks that they aim to improve. We identify the desired properties (i.e., inductive biases) of each kind of embedding and discuss some potential future work.
Modeling Relational Patterns for Logical Query Answering over Knowledge Graphs
Mar 21, 2023Abstract:Answering first-order logical (FOL) queries over knowledge graphs (KG) remains a challenging task mainly due to KG incompleteness. Query embedding approaches this problem by computing the low-dimensional vector representations of entities, relations, and logical queries. KGs exhibit relational patterns such as symmetry and composition and modeling the patterns can further enhance the performance of query embedding models. However, the role of such patterns in answering FOL queries by query embedding models has not been yet studied in the literature. In this paper, we fill in this research gap and empower FOL queries reasoning with pattern inference by introducing an inductive bias that allows for learning relation patterns. To this end, we develop a novel query embedding method, RoConE, that defines query regions as geometric cones and algebraic query operators by rotations in complex space. RoConE combines the advantages of Cone as a well-specified geometric representation for query embedding, and also the rotation operator as a powerful algebraic operation for pattern inference. Our experimental results on several benchmark datasets confirm the advantage of relational patterns for enhancing logical query answering task.
Graph Attention with Hierarchies for Multi-hop Question Answering
Jan 27, 2023Abstract:Multi-hop QA (Question Answering) is the task of finding the answer to a question across multiple documents. In recent years, a number of Deep Learning-based approaches have been proposed to tackle this complex task, as well as a few standard benchmarks to assess models Multi-hop QA capabilities. In this paper, we focus on the well-established HotpotQA benchmark dataset, which requires models to perform answer span extraction as well as support sentence prediction. We present two extensions to the SOTA Graph Neural Network (GNN) based model for HotpotQA, Hierarchical Graph Network (HGN): (i) we complete the original hierarchical structure by introducing new edges between the query and context sentence nodes; (ii) in the graph propagation step, we propose a novel extension to Hierarchical Graph Attention Network GATH (Graph ATtention with Hierarchies) that makes use of the graph hierarchy to update the node representations in a sequential fashion. Experiments on HotpotQA demonstrate the efficiency of the proposed modifications and support our assumptions about the effects of model related variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge