Transition role of entangled data in quantum machine learning

Entanglement serves as the resource to empower quantum computing. Recent progress has highlighted its positive impact on learning quantum dynamics, wherein the integration of entanglement into quantum operations or measurements of quantum machine learning (QML) models leads to substantial reductions in training data size, surpassing a specified prediction error threshold. However, an analytical understanding of how the entanglement degree in data affects model performance remains elusive. In this study, we address this knowledge gap by establishing a quantum no-free-lunch (NFL) theorem for learning quantum dynamics using entangled data. Contrary to previous findings, we prove that the impact of entangled data on prediction error exhibits a dual effect, depending on the number of permitted measurements. With a sufficient number of measurements, increasing the entanglement of training data consistently reduces the prediction error or decreases the required size of the training data to achieve the same prediction error. Conversely, when few measurements are allowed, employing highly entangled data could lead to an increased prediction error. The achieved results provide critical guidance for designing advanced QML protocols, especially for those tailored for execution on early-stage quantum computers with limited access to quantum resources.

Theory of Quantum Generative Learning Models with Maximum Mean Discrepancy

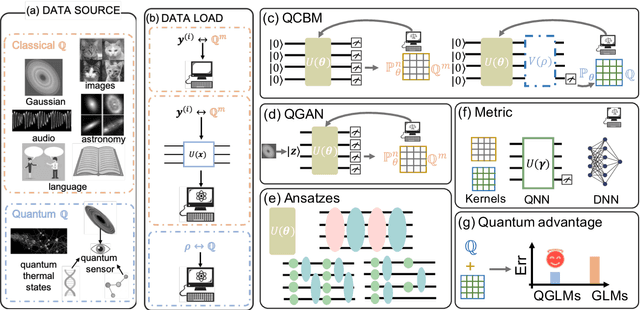
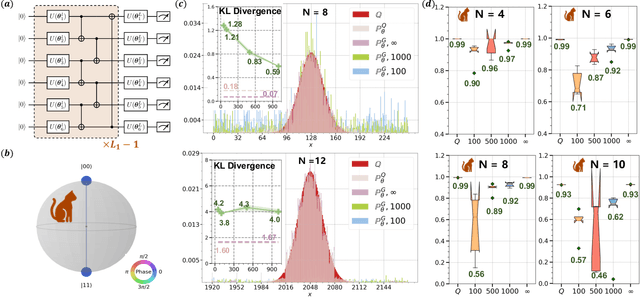
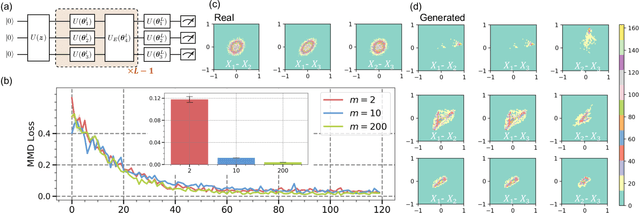
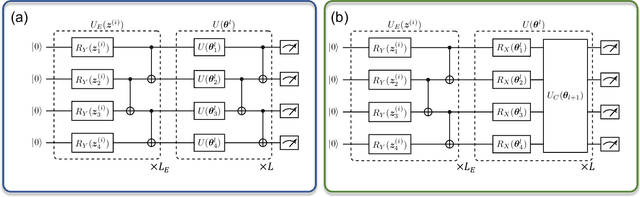
The intrinsic probabilistic nature of quantum mechanics invokes endeavors of designing quantum generative learning models (QGLMs) with computational advantages over classical ones. To date, two prototypical QGLMs are quantum circuit Born machines (QCBMs) and quantum generative adversarial networks (QGANs), which approximate the target distribution in explicit and implicit ways, respectively. Despite the empirical achievements, the fundamental theory of these models remains largely obscure. To narrow this knowledge gap, here we explore the learnability of QCBMs and QGANs from the perspective of generalization when their loss is specified to be the maximum mean discrepancy. Particularly, we first analyze the generalization ability of QCBMs and identify their superiorities when the quantum devices can directly access the target distribution and the quantum kernels are employed. Next, we prove how the generalization error bound of QGANs depends on the employed Ansatz, the number of qudits, and input states. This bound can be further employed to seek potential quantum advantages in Hamiltonian learning tasks. Numerical results of QGLMs in approximating quantum states, Gaussian distribution, and ground states of parameterized Hamiltonians accord with the theoretical analysis. Our work opens the avenue for quantitatively understanding the power of quantum generative learning models.

Few-shot Backdoor Defense Using Shapley Estimation

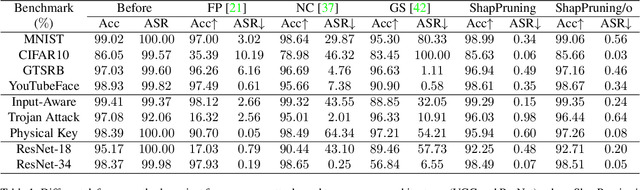
Deep neural networks have achieved impressive performance in a variety of tasks over the last decade, such as autonomous driving, face recognition, and medical diagnosis. However, prior works show that deep neural networks are easily manipulated into specific, attacker-decided behaviors in the inference stage by backdoor attacks which inject malicious small hidden triggers into model training, raising serious security threats. To determine the triggered neurons and protect against backdoor attacks, we exploit Shapley value and develop a new approach called Shapley Pruning (ShapPruning) that successfully mitigates backdoor attacks from models in a data-insufficient situation (1 image per class or even free of data). Considering the interaction between neurons, ShapPruning identifies the few infected neurons (under 1% of all neurons) and manages to protect the model's structure and accuracy after pruning as many infected neurons as possible. To accelerate ShapPruning, we further propose discarding threshold and $\epsilon$-greedy strategy to accelerate Shapley estimation, making it possible to repair poisoned models with only several minutes. Experiments demonstrate the effectiveness and robustness of our method against various attacks and tasks compared to existing methods.

Spatial-Temporal-Fusion BNN: Variational Bayesian Feature Layer

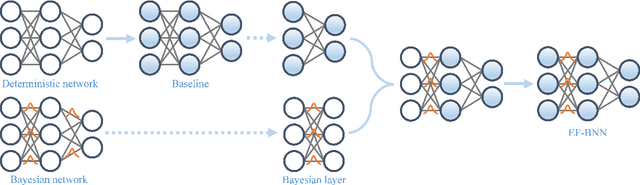
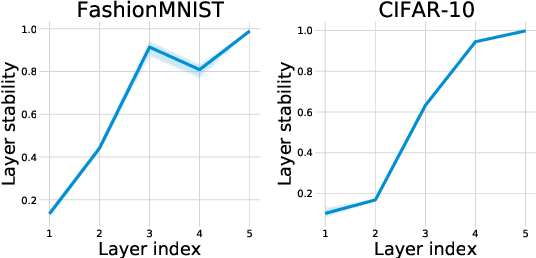
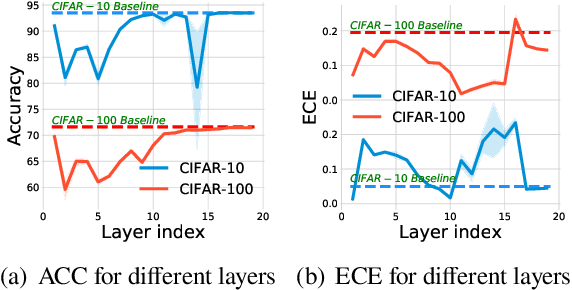
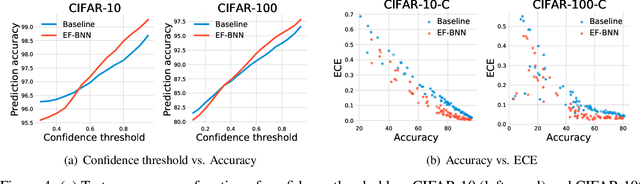
Bayesian neural networks (BNNs) have become a principal approach to alleviate overconfident predictions in deep learning, but they often suffer from scaling issues due to a large number of distribution parameters. In this paper, we discover that the first layer of a deep network possesses multiple disparate optima when solely retrained. This indicates a large posterior variance when the first layer is altered by a Bayesian layer, which motivates us to design a spatial-temporal-fusion BNN (STF-BNN) for efficiently scaling BNNs to large models: (1) first normally train a neural network from scratch to realize fast training; and (2) the first layer is converted to Bayesian and inferred by employing stochastic variational inference, while other layers are fixed. Compared to vanilla BNNs, our approach can greatly reduce the training time and the number of parameters, which contributes to scale BNNs efficiently. We further provide theoretical guarantees on the generalizability and the capability of mitigating overconfidence of STF-BNN. Comprehensive experiments demonstrate that STF-BNN (1) achieves the state-of-the-art performance on prediction and uncertainty quantification; (2) significantly improves adversarial robustness and privacy preservation; and (3) considerably reduces training time and memory costs.

Towards Defending Multiple Adversarial Perturbations via Gated Batch Normalization

There is now extensive evidence demonstrating that deep neural networks are vulnerable to adversarial examples, motivating the development of defenses against adversarial attacks. However, existing adversarial defenses typically improve model robustness against individual specific perturbation types. Some recent methods improve model robustness against adversarial attacks in multiple $\ell_p$ balls, but their performance against each perturbation type is still far from satisfactory. To better understand this phenomenon, we propose the \emph{multi-domain} hypothesis, stating that different types of adversarial perturbations are drawn from different domains. Guided by the multi-domain hypothesis, we propose \emph{Gated Batch Normalization (GBN)}, a novel building block for deep neural networks that improves robustness against multiple perturbation types. GBN consists of a gated sub-network and a multi-branch batch normalization (BN) layer, where the gated sub-network separates different perturbation types, and each BN branch is in charge of a single perturbation type and learns domain-specific statistics for input transformation. Then, features from different branches are aligned as domain-invariant representations for the subsequent layers. We perform extensive evaluations of our approach on MNIST, CIFAR-10, and Tiny-ImageNet, and demonstrate that GBN outperforms previous defense proposals against multiple perturbation types, i.e, $\ell_1$, $\ell_2$, and $\ell_{\infty}$ perturbations, by large margins of 10-20\%.

Explicitly Learning Topology for Differentiable Neural Architecture Search

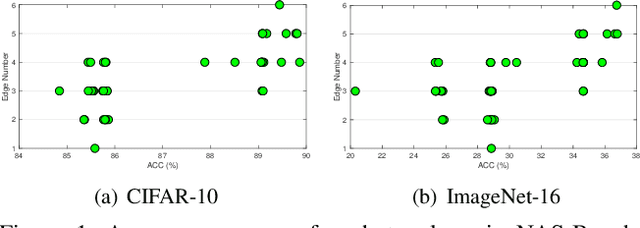
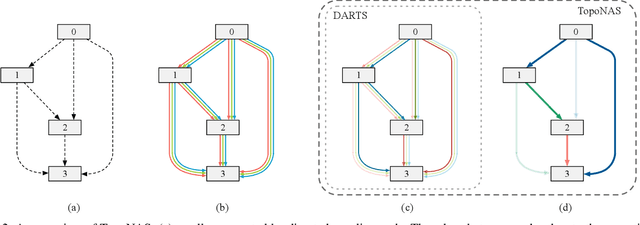
Differentiable neural architecture search (DARTS) has gained much success in discovering more flexible and diverse cell types. Current methods couple the operations and topology during search, and simply derive optimal topology by a hand-craft rule. However, topology also matters for neural architectures since it controls the interactions between features of operations. In this paper, we highlight the topology learning in differentiable NAS, and propose an explicit topology modeling method, named TopoNAS, to directly decouple the operation selection and topology during search. Concretely, we introduce a set of topological variables and a combinatorial probabilistic distribution to explicitly indicate the target topology. Besides, we also leverage a passive-aggressive regularization to suppress invalid topology within supernet. Our introduced topological variables can be jointly learned with operation variables and supernet weights, and apply to various DARTS variants. Extensive experiments on CIFAR-10 and ImageNet validate the effectiveness of our proposed TopoNAS. The results show that TopoNAS does enable to search cells with more diverse and complex topology, and boost the performance significantly. For example, TopoNAS can improve DARTS by 0.16\% accuracy on CIFAR-10 dataset with 40\% parameters reduced or 0.35\% with similar parameters.

Theoretical Analysis of Adversarial Learning: A Minimax Approach

We propose a general theoretical method for analyzing the risk bound in the presence of adversaries. In particular, we try to fit the adversarial learning problem into the minimax framework. We first show that the original adversarial learning problem could be reduced to a minimax statistical learning problem by introducing a transport map between distributions. Then we prove a risk bound for this minimax problem in terms of covering numbers. In contrast to previous minimax bounds in \cite{lee,far}, our bound is informative when the radius of the ambiguity set is small. Our method could be applied to multi-class classification problems and commonly-used loss functions such as hinge loss and ramp loss. As two illustrative examples, we derive the adversarial risk bounds for kernel-SVM and deep neural networks. Our results indicate that a stronger adversary might have a negative impact on the complexity of the hypothesis class and the existence of margin could serve as a defense mechanism to counter adversarial attacks.