Bujiao Wu
Theory of Quantum Generative Learning Models with Maximum Mean Discrepancy
May 10, 2022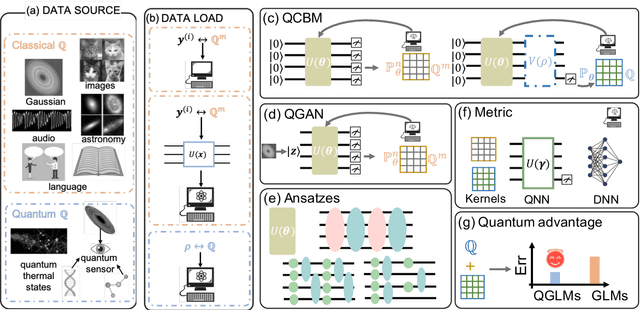
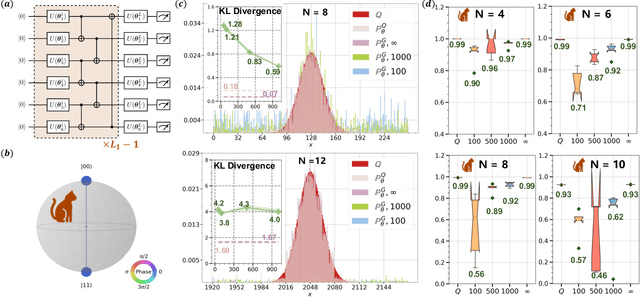
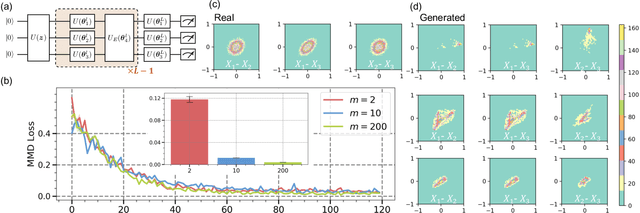
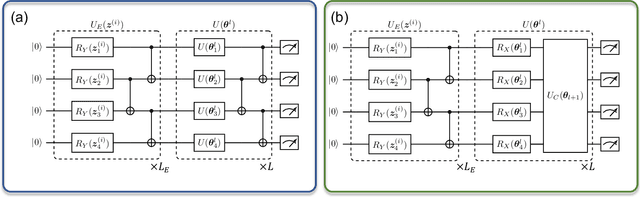
Abstract:The intrinsic probabilistic nature of quantum mechanics invokes endeavors of designing quantum generative learning models (QGLMs) with computational advantages over classical ones. To date, two prototypical QGLMs are quantum circuit Born machines (QCBMs) and quantum generative adversarial networks (QGANs), which approximate the target distribution in explicit and implicit ways, respectively. Despite the empirical achievements, the fundamental theory of these models remains largely obscure. To narrow this knowledge gap, here we explore the learnability of QCBMs and QGANs from the perspective of generalization when their loss is specified to be the maximum mean discrepancy. Particularly, we first analyze the generalization ability of QCBMs and identify their superiorities when the quantum devices can directly access the target distribution and the quantum kernels are employed. Next, we prove how the generalization error bound of QGANs depends on the employed Ansatz, the number of qudits, and input states. This bound can be further employed to seek potential quantum advantages in Hamiltonian learning tasks. Numerical results of QGLMs in approximating quantum states, Gaussian distribution, and ground states of parameterized Hamiltonians accord with the theoretical analysis. Our work opens the avenue for quantitatively understanding the power of quantum generative learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge