Xiao Yuan
Coreset selection can accelerate quantum machine learning models with provable generalization
Sep 19, 2023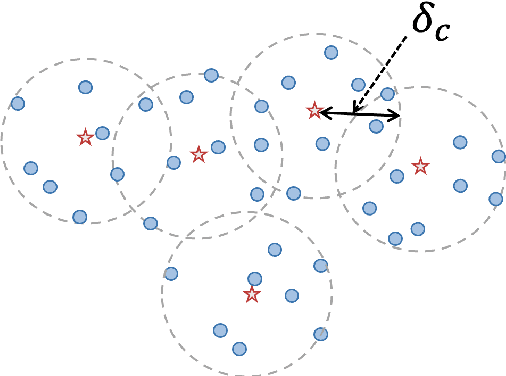
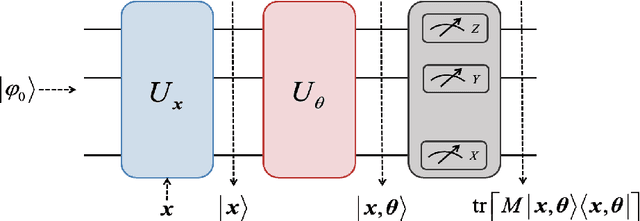
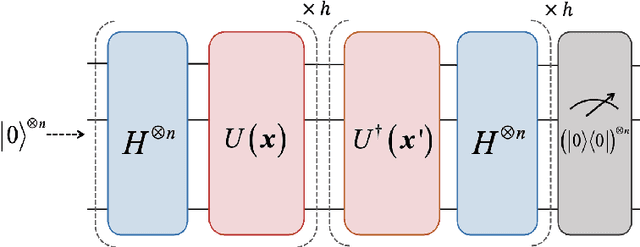
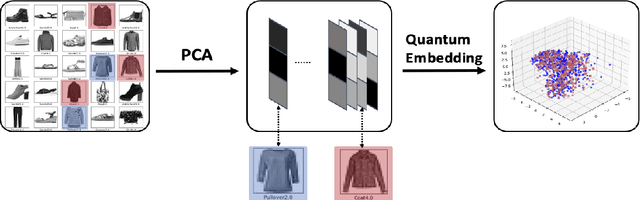
Abstract:Quantum neural networks (QNNs) and quantum kernels stand as prominent figures in the realm of quantum machine learning, poised to leverage the nascent capabilities of near-term quantum computers to surmount classical machine learning challenges. Nonetheless, the training efficiency challenge poses a limitation on both QNNs and quantum kernels, curbing their efficacy when applied to extensive datasets. To confront this concern, we present a unified approach: coreset selection, aimed at expediting the training of QNNs and quantum kernels by distilling a judicious subset from the original training dataset. Furthermore, we analyze the generalization error bounds of QNNs and quantum kernels when trained on such coresets, unveiling the comparable performance with those training on the complete original dataset. Through systematic numerical simulations, we illuminate the potential of coreset selection in expediting tasks encompassing synthetic data classification, identification of quantum correlations, and quantum compiling. Our work offers a useful way to improve diverse quantum machine learning models with a theoretical guarantee while reducing the training cost.
BeeTLe: A Framework for Linear B-Cell Epitope Prediction and Classification
Sep 05, 2023Abstract:The process of identifying and characterizing B-cell epitopes, which are the portions of antigens recognized by antibodies, is important for our understanding of the immune system, and for many applications including vaccine development, therapeutics, and diagnostics. Computational epitope prediction is challenging yet rewarding as it significantly reduces the time and cost of laboratory work. Most of the existing tools do not have satisfactory performance and only discriminate epitopes from non-epitopes. This paper presents a new deep learning-based multi-task framework for linear B-cell epitope prediction as well as antibody type-specific epitope classification. Specifically, a sequenced-based neural network model using recurrent layers and Transformer blocks is developed. We propose an amino acid encoding method based on eigen decomposition to help the model learn the representations of epitopes. We introduce modifications to standard cross-entropy loss functions by extending a logit adjustment technique to cope with the class imbalance. Experimental results on data curated from the largest public epitope database demonstrate the validity of the proposed methods and the superior performance compared to competing ones.
Transition role of entangled data in quantum machine learning
Jun 06, 2023Abstract:Entanglement serves as the resource to empower quantum computing. Recent progress has highlighted its positive impact on learning quantum dynamics, wherein the integration of entanglement into quantum operations or measurements of quantum machine learning (QML) models leads to substantial reductions in training data size, surpassing a specified prediction error threshold. However, an analytical understanding of how the entanglement degree in data affects model performance remains elusive. In this study, we address this knowledge gap by establishing a quantum no-free-lunch (NFL) theorem for learning quantum dynamics using entangled data. Contrary to previous findings, we prove that the impact of entangled data on prediction error exhibits a dual effect, depending on the number of permitted measurements. With a sufficient number of measurements, increasing the entanglement of training data consistently reduces the prediction error or decreases the required size of the training data to achieve the same prediction error. Conversely, when few measurements are allowed, employing highly entangled data could lead to an increased prediction error. The achieved results provide critical guidance for designing advanced QML protocols, especially for those tailored for execution on early-stage quantum computers with limited access to quantum resources.
Theory of Quantum Generative Learning Models with Maximum Mean Discrepancy
May 10, 2022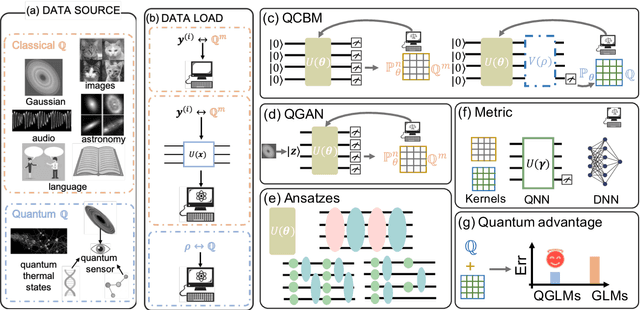
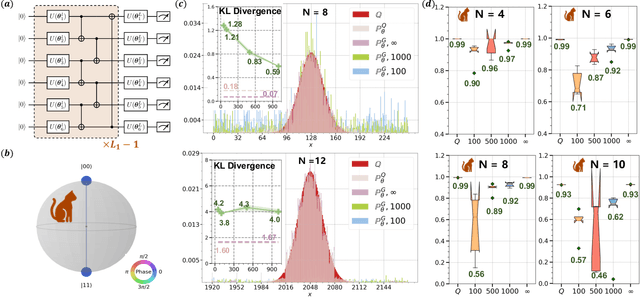
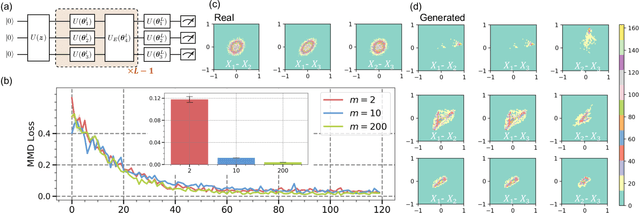
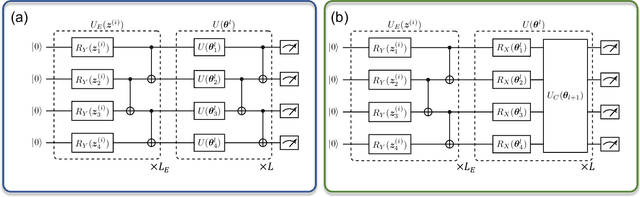
Abstract:The intrinsic probabilistic nature of quantum mechanics invokes endeavors of designing quantum generative learning models (QGLMs) with computational advantages over classical ones. To date, two prototypical QGLMs are quantum circuit Born machines (QCBMs) and quantum generative adversarial networks (QGANs), which approximate the target distribution in explicit and implicit ways, respectively. Despite the empirical achievements, the fundamental theory of these models remains largely obscure. To narrow this knowledge gap, here we explore the learnability of QCBMs and QGANs from the perspective of generalization when their loss is specified to be the maximum mean discrepancy. Particularly, we first analyze the generalization ability of QCBMs and identify their superiorities when the quantum devices can directly access the target distribution and the quantum kernels are employed. Next, we prove how the generalization error bound of QGANs depends on the employed Ansatz, the number of qudits, and input states. This bound can be further employed to seek potential quantum advantages in Hamiltonian learning tasks. Numerical results of QGLMs in approximating quantum states, Gaussian distribution, and ground states of parameterized Hamiltonians accord with the theoretical analysis. Our work opens the avenue for quantitatively understanding the power of quantum generative learning models.
Towards a variational Jordan-Lee-Preskill quantum algorithm
Sep 28, 2021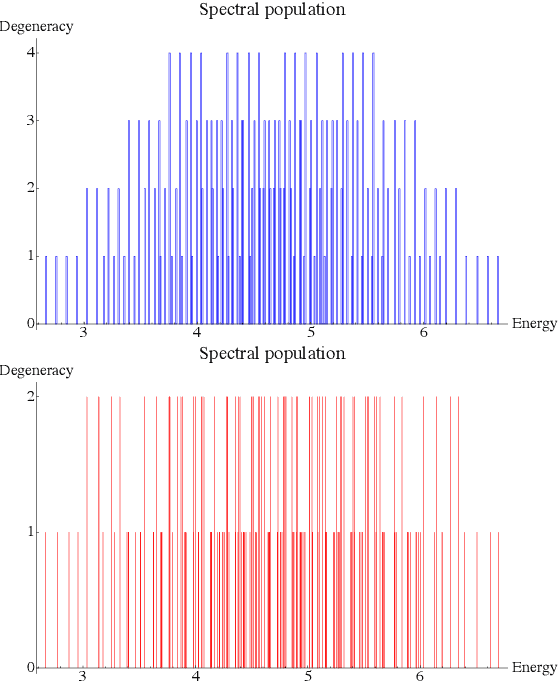
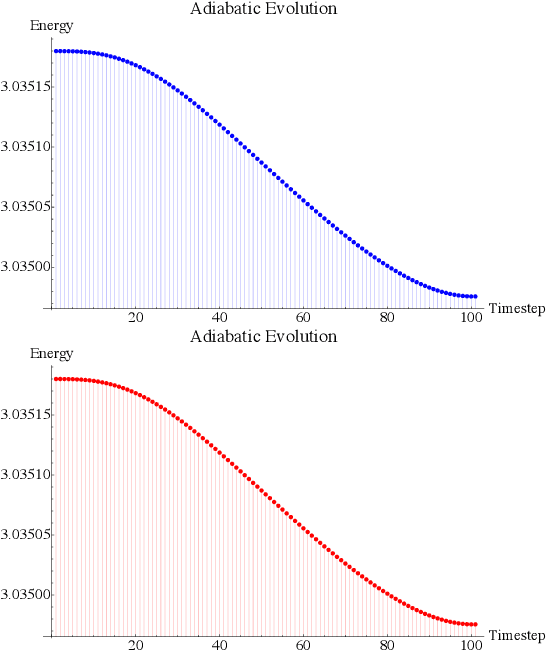
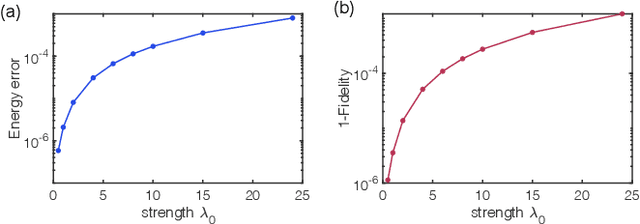
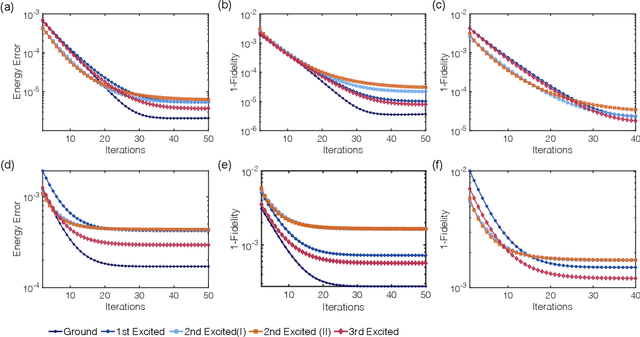
Abstract:Rapid developments of quantum information technology show promising opportunities for simulating quantum field theory in near-term quantum devices. In this work, we formulate the theory of (time-dependent) variational quantum simulation, explicitly designed for quantum simulation of quantum field theory. We develop hybrid quantum-classical algorithms for crucial ingredients in particle scattering experiments, including encoding, state preparation, and time evolution, with several numerical simulations to demonstrate our algorithms in the 1+1 dimensional $\lambda \phi^4$ quantum field theory. These algorithms could be understood as near-term analogs of the Jordan-Lee-Preskill algorithm, the basic algorithm for simulating quantum field theory using universal quantum devices. Our contribution also includes a bosonic version of the Unitary Coupled Cluster ansatz with physical interpretation in quantum field theory, a discussion about the subspace fidelity, a comparison among different bases in the 1+1 dimensional $\lambda \phi^4$ theory, and the "spectral crowding" in the quantum field theory simulation.
Variational Quantum Algorithms
Dec 16, 2020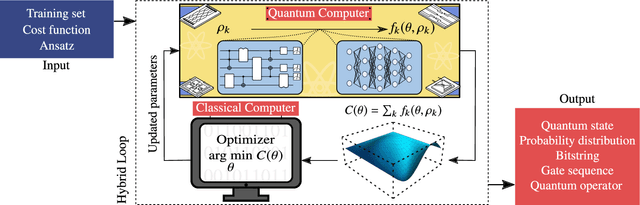
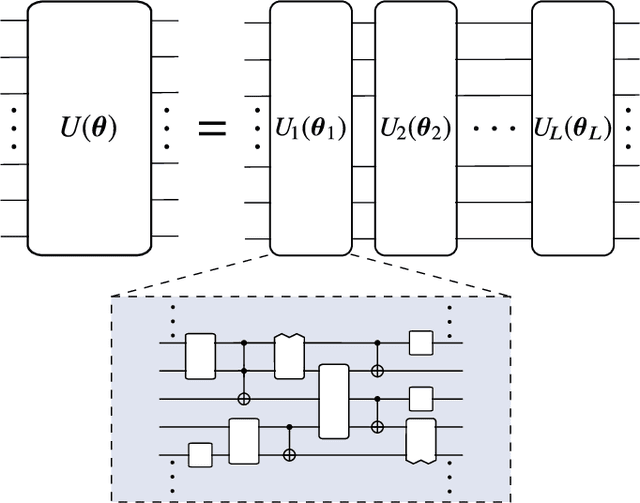
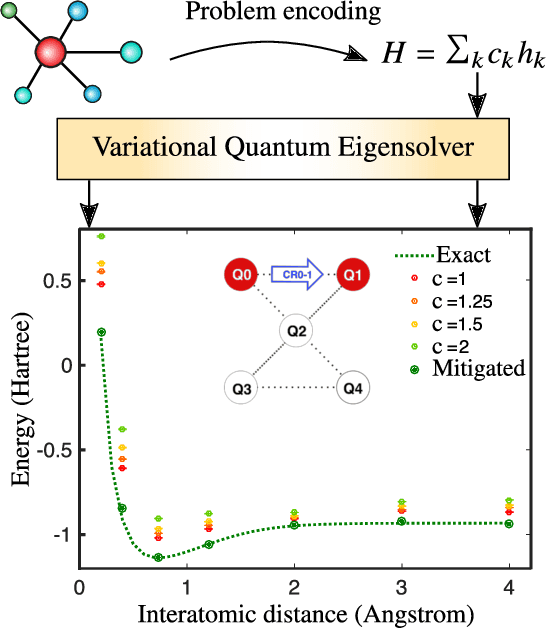
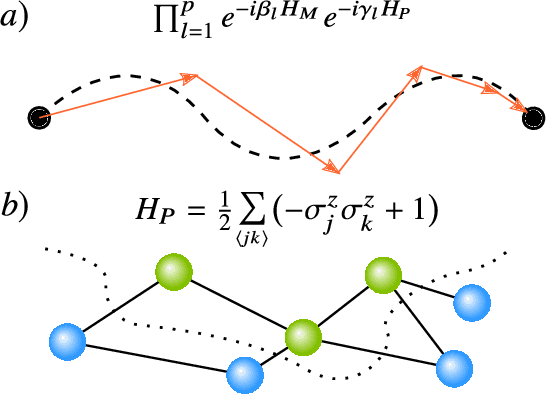
Abstract:Applications such as simulating large quantum systems or solving large-scale linear algebra problems are immensely challenging for classical computers due their extremely high computational cost. Quantum computers promise to unlock these applications, although fault-tolerant quantum computers will likely not be available for several years. Currently available quantum devices have serious constraints, including limited qubit numbers and noise processes that limit circuit depth. Variational Quantum Algorithms (VQAs), which employ a classical optimizer to train a parametrized quantum circuit, have emerged as a leading strategy to address these constraints. VQAs have now been proposed for essentially all applications that researchers have envisioned for quantum computers, and they appear to the best hope for obtaining quantum advantage. Nevertheless, challenges remain including the trainability, accuracy, and efficiency of VQAs. In this review article we present an overview of the field of VQAs. Furthermore, we discuss strategies to overcome their challenges as well as the exciting prospects for using them as a means to obtain quantum advantage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge