Asymptotic FDR Control with Model-X Knockoffs: Is Moments Matching Sufficient?

We propose a unified theoretical framework for studying the robustness of the model-X knockoffs framework by investigating the asymptotic false discovery rate (FDR) control of the practically implemented approximate knockoffs procedure. This procedure deviates from the model-X knockoffs framework by substituting the true covariate distribution with a user-specified distribution that can be learned using in-sample observations. By replacing the distributional exchangeability condition of the model-X knockoff variables with three conditions on the approximate knockoff statistics, we establish that the approximate knockoffs procedure achieves the asymptotic FDR control. Using our unified framework, we further prove that an arguably most popularly used knockoff variable generation method--the Gaussian knockoffs generator based on the first two moments matching--achieves the asymptotic FDR control when the two-moment-based knockoff statistics are employed in the knockoffs inference procedure. For the first time in the literature, our theoretical results justify formally the effectiveness and robustness of the Gaussian knockoffs generator. Simulation and real data examples are conducted to validate the theoretical findings.

ARK: Robust Knockoffs Inference with Coupling

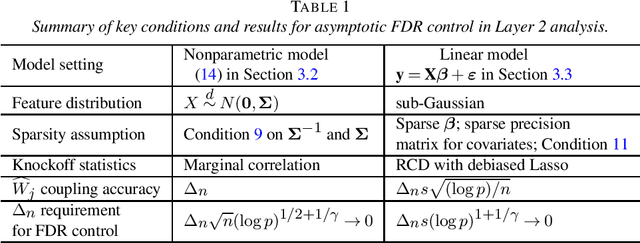
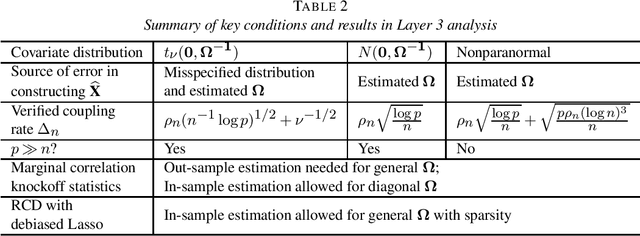
We investigate the robustness of the model-X knockoffs framework with respect to the misspecified or estimated feature distribution. We achieve such a goal by theoretically studying the feature selection performance of a practically implemented knockoffs algorithm, which we name as the approximate knockoffs (ARK) procedure, under the measures of the false discovery rate (FDR) and family wise error rate (FWER). The approximate knockoffs procedure differs from the model-X knockoffs procedure only in that the former uses the misspecified or estimated feature distribution. A key technique in our theoretical analyses is to couple the approximate knockoffs procedure with the model-X knockoffs procedure so that random variables in these two procedures can be close in realizations. We prove that if such coupled model-X knockoffs procedure exists, the approximate knockoffs procedure can achieve the asymptotic FDR or FWER control at the target level. We showcase three specific constructions of such coupled model-X knockoff variables, verifying their existence and justifying the robustness of the model-X knockoffs framework.