Asymptotic FDR Control with Model-X Knockoffs: Is Moments Matching Sufficient?

We propose a unified theoretical framework for studying the robustness of the model-X knockoffs framework by investigating the asymptotic false discovery rate (FDR) control of the practically implemented approximate knockoffs procedure. This procedure deviates from the model-X knockoffs framework by substituting the true covariate distribution with a user-specified distribution that can be learned using in-sample observations. By replacing the distributional exchangeability condition of the model-X knockoff variables with three conditions on the approximate knockoff statistics, we establish that the approximate knockoffs procedure achieves the asymptotic FDR control. Using our unified framework, we further prove that an arguably most popularly used knockoff variable generation method--the Gaussian knockoffs generator based on the first two moments matching--achieves the asymptotic FDR control when the two-moment-based knockoff statistics are employed in the knockoffs inference procedure. For the first time in the literature, our theoretical results justify formally the effectiveness and robustness of the Gaussian knockoffs generator. Simulation and real data examples are conducted to validate the theoretical findings.

Gradient descent inference in empirical risk minimization

Gradient descent is one of the most widely used iterative algorithms in modern statistical learning. However, its precise algorithmic dynamics in high-dimensional settings remain only partially understood, which has therefore limited its broader potential for statistical inference applications. This paper provides a precise, non-asymptotic distributional characterization of gradient descent iterates in a broad class of empirical risk minimization problems, in the so-called mean-field regime where the sample size is proportional to the signal dimension. Our non-asymptotic state evolution theory holds for both general non-convex loss functions and non-Gaussian data, and reveals the central role of two Onsager correction matrices that precisely characterize the non-trivial dependence among all gradient descent iterates in the mean-field regime. Although the Onsager correction matrices are typically analytically intractable, our state evolution theory facilitates a generic gradient descent inference algorithm that consistently estimates these matrices across a broad class of models. Leveraging this algorithm, we show that the state evolution can be inverted to construct (i) data-driven estimators for the generalization error of gradient descent iterates and (ii) debiased gradient descent iterates for inference of the unknown signal. Detailed applications to two canonical models--linear regression and (generalized) logistic regression--are worked out to illustrate model-specific features of our general theory and inference methods.

On the Precise Asymptotics and Refined Regret of the Variance-Aware UCB Algorithm

In this paper, we study the behavior of the Upper Confidence Bound-Variance (UCB-V) algorithm for Multi-Armed Bandit (MAB) problems, a variant of the canonical Upper Confidence Bound (UCB) algorithm that incorporates variance estimates into its decision-making process. More precisely, we provide an asymptotic characterization of the arm-pulling rates of UCB-V, extending recent results for the canonical UCB in Kalvit and Zeevi (2021) and Khamaru and Zhang (2024). In an interesting contrast to the canonical UCB, we show that the behavior of UCB-V can exhibit instability, meaning that the arm-pulling rates may not always be asymptotically deterministic. Besides the asymptotic characterization, we also provide non-asymptotic bounds for arm-pulling rates in the high probability regime, offering insights into regret analysis. As an application of this high probability result, we show that UCB-V can achieve a refined regret bound, previously unknown even for more complicate and advanced variance-aware online decision-making algorithms.

Improving Global Forest Mapping by Semi-automatic Sample Labeling with Deep Learning on Google Earth Images

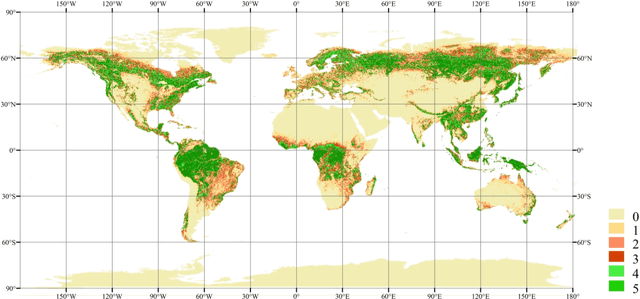
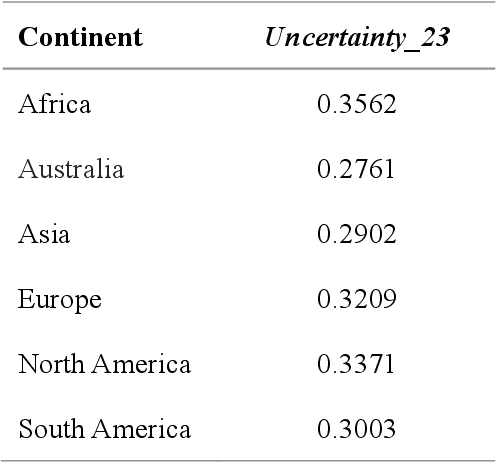
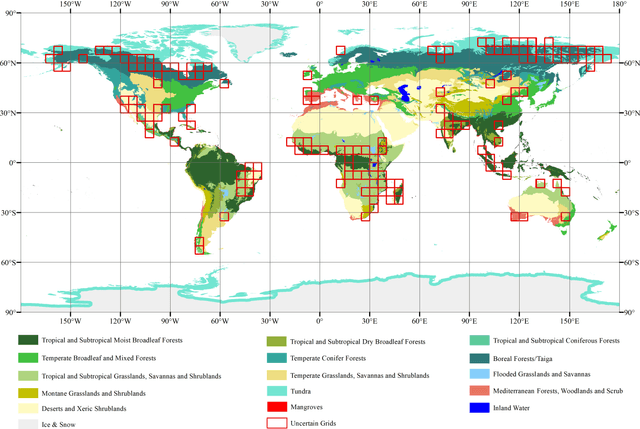
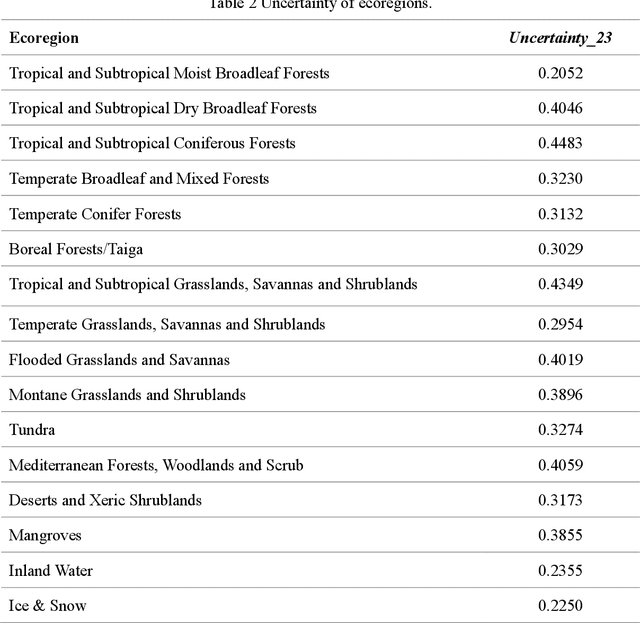
Global forest cover is critical to the provision of certain ecosystem services. With the advent of the google earth engine cloud platform, fine resolution global land cover mapping task could be accomplished in a matter of days instead of years. The amount of global forest cover (GFC) products has been steadily increasing in the last decades. However, it's hard for users to select suitable one due to great differences between these products, and the accuracy of these GFC products has not been verified on global scale. To provide guidelines for users and producers, it is urgent to produce a validation sample set at the global level. However, this labeling task is time and labor consuming, which has been the main obstacle to the progress of global land cover mapping. In this research, a labor-efficient semi-automatic framework is introduced to build a biggest ever Forest Sample Set (FSS) contained 395280 scattered samples categorized as forest, shrubland, grassland, impervious surface, etc. On the other hand, to provide guidelines for the users, we comprehensively validated the local and global mapping accuracy of all existing 30m GFC products, and analyzed and mapped the agreement of them. Moreover, to provide guidelines for the producers, optimal sampling strategy was proposed to improve the global forest classification. Furthermore, a new global forest cover named GlobeForest2020 has been generated, which proved to improve the previous highest state-of-the-art accuracies (obtained by Gong et al., 2017) by 2.77% in uncertain grids and by 1.11% in certain grids.