Asymptotic Optimality for Decentralised Bandits

We consider a large number of agents collaborating on a multi-armed bandit problem with a large number of arms. The goal is to minimise the regret of each agent in a communication-constrained setting. We present a decentralised algorithm which builds upon and improves the Gossip-Insert-Eliminate method of Chawla et al. arxiv:2001.05452. We provide a theoretical analysis of the regret incurred which shows that our algorithm is asymptotically optimal. In fact, our regret guarantee matches the asymptotically optimal rate achievable in the full communication setting. Finally, we present empirical results which support our conclusions

Optimal subgroup selection

In clinical trials and other applications, we often see regions of the feature space that appear to exhibit interesting behaviour, but it is unclear whether these observed phenomena are reflected at the population level. Focusing on a regression setting, we consider the subgroup selection challenge of identifying a region of the feature space on which the regression function exceeds a pre-determined threshold. We formulate the problem as one of constrained optimisation, where we seek a low-complexity, data-dependent selection set on which, with a guaranteed probability, the regression function is uniformly at least as large as the threshold; subject to this constraint, we would like the region to contain as much mass under the marginal feature distribution as possible. This leads to a natural notion of regret, and our main contribution is to determine the minimax optimal rate for this regret in both the sample size and the Type I error probability. The rate involves a delicate interplay between parameters that control the smoothness of the regression function, as well as exponents that quantify the extent to which the optimal selection set at the population level can be approximated by families of well-behaved subsets. Finally, we expand the scope of our previous results by illustrating how they may be generalised to a treatment and control setting, where interest lies in the heterogeneous treatment effect.

Adaptive transfer learning

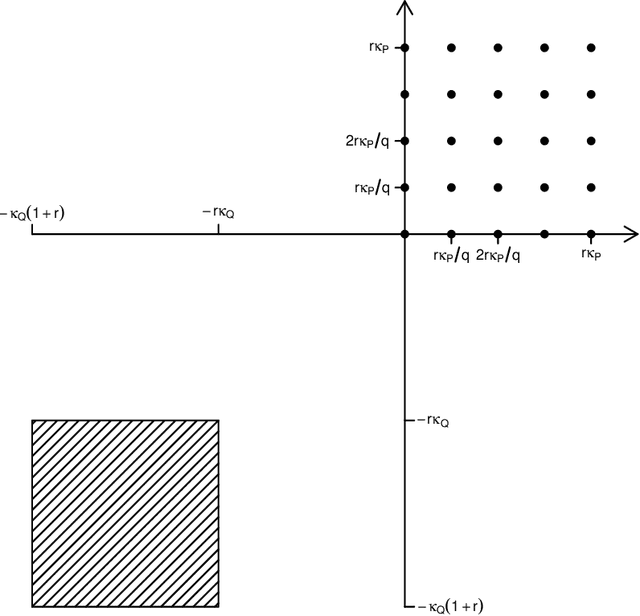
In transfer learning, we wish to make inference about a target population when we have access to data both from the distribution itself, and from a different but related source distribution. We introduce a flexible framework for transfer learning in the context of binary classification, allowing for covariate-dependent relationships between the source and target distributions that are not required to preserve the Bayes decision boundary. Our main contributions are to derive the minimax optimal rates of convergence (up to poly-logarithmic factors) in this problem, and show that the optimal rate can be achieved by an algorithm that adapts to key aspects of the unknown transfer relationship, as well as the smoothness and tail parameters of our distributional classes. This optimal rate turns out to have several regimes, depending on the interplay between the relative sample sizes and the strength of the transfer relationship, and our algorithm achieves optimality by careful, decision tree-based calibration of local nearest-neighbour procedures.

Statistical optimality conditions for compressive ensembles

We present a framework for the theoretical analysis of ensembles of low-complexity empirical risk minimisers trained on independent random compressions of high-dimensional data. First we introduce a general distribution-dependent upper-bound on the excess risk, framed in terms of a natural notion of compressibility. This bound is independent of the dimension of the original data representation, and explains the in-built regularisation effect of the compressive approach. We then instantiate this general bound to classification and regression tasks, considering Johnson-Lindenstrauss mappings as the compression scheme. For each of these tasks, our strategy is to develop a tight upper bound on the compressibility function, and by doing so we discover distributional conditions of geometric nature under which the compressive algorithm attains minimax-optimal rates up to at most poly-logarithmic factors. In the case of compressive classification, this is achieved with a mild geometric margin condition along with a flexible moment condition that is significantly more general than the assumption of bounded domain. In the case of regression with strongly convex smooth loss functions we find that compressive regression is capable of exploiting spectral decay with near-optimal guarantees. In addition, a key ingredient for our central upper bound is a high probability uniform upper bound on the integrated deviation of dependent empirical processes, which may be of independent interest.

Fast Rates for a kNN Classifier Robust to Unknown Asymmetric Label Noise

We consider classification in the presence of class-dependent asymmetric label noise with unknown noise probabilities. In this setting, identifiability conditions are known, but additional assumptions were shown to be required for finite sample rates, and so far only the parametric rate has been obtained. Assuming these identifiability conditions, together with a measure-smoothness condition on the regression function and Tsybakov's margin condition, we show that the Robust kNN classifier of Gao et al. attains, the minimax optimal rates of the noise-free setting, up to a log factor, even when trained on data with unknown asymmetric label noise. Hence, our results provide a solid theoretical backing for this empirically successful algorithm. By contrast the standard kNN is not even consistent in the setting of asymmetric label noise. A key idea in our analysis is a simple kNN based method for estimating the maximum of a function that requires far less assumptions than existing mode estimators do, and which may be of independent interest for noise proportion estimation and randomised optimisation problems.