A Definition of Non-Stationary Bandits

The subject of non-stationary bandit learning has attracted much recent attention. However, non-stationary bandits lack a formal definition. Loosely speaking, non-stationary bandits have typically been characterized in the literature as those for which the reward distribution changes over time. We demonstrate that this informal definition is ambiguous. Further, a widely-used notion of regret -- the dynamic regret -- is motivated by this ambiguous definition and thus problematic. In particular, even for an optimal agent, dynamic regret can suggest poor performance. The ambiguous definition also motivates a measure of the degree of non-stationarity experienced by a bandit, which often overestimates and can give rise to extremely loose regret bounds. The primary contribution of this paper is a formal definition that resolves ambiguity. This definition motivates a new notion of regret, an alternative measure of the degree of non-stationarity, and a regret analysis that leads to tighter bounds for non-stationary bandit learning. The regret analysis applies to any bandit, stationary or non-stationary, and any agent.

Nonstationary Bandit Learning via Predictive Sampling

We propose predictive sampling as an approach to selecting actions that balance between exploration and exploitation in nonstationary bandit environments. When specialized to stationary environments, predictive sampling is equivalent to Thompson sampling. However, predictive sampling is effective across a range of nonstationary environments in which Thompson sampling suffers. We establish a general information-theoretic bound on the Bayesian regret of predictive sampling. We then specialize this bound to study a modulated Bernoulli bandit environment. Our analysis highlights a key advantage of predictive sampling over Thompson sampling: predictive sampling deprioritizes investments in exploration where acquired information will quickly become less relevant.

Gaussian Imagination in Bandit Learning

Assuming distributions are Gaussian often facilitates computations that are otherwise intractable. We study the performance of an agent that attains a bounded information ratio with respect to a bandit environment with a Gaussian prior distribution and a Gaussian likelihood function when applied instead to a Bernoulli bandit. Relative to an information-theoretic bound on the Bayesian regret the agent would incur when interacting with the Gaussian bandit, we bound the increase in regret when the agent interacts with the Bernoulli bandit. If the Gaussian prior distribution and likelihood function are sufficiently diffuse, this increase grows at a rate which is at most linear in the square-root of the time horizon, and thus the per-timestep increase vanishes. Our results formalize the folklore that so-called Bayesian agents remain effective when instantiated with diffuse misspecified distributions.

Learning and Information in Stochastic Networks and Queues

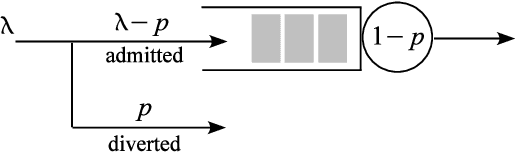
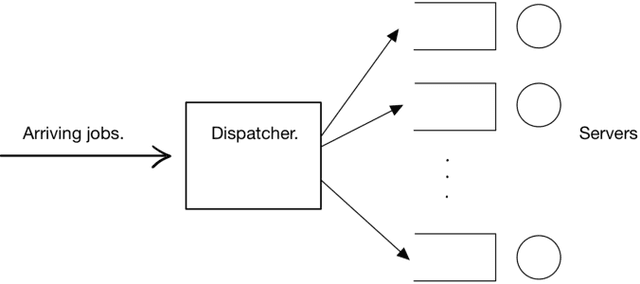
We review the role of information and learning in the stability and optimization of queueing systems. In recent years, techniques from supervised learning, bandit learning and reinforcement learning have been applied to queueing systems supported by increasing role of information in decision making. We present observations and new results that help rationalize the application of these areas to queueing systems. We prove that the MaxWeight and BackPressure policies are an application of Blackwell's Approachability Theorem. This connects queueing theoretic results with adversarial learning. We then discuss the requirements of statistical learning for service parameter estimation. As an example, we show how queue size regret can be bounded when applying a perceptron algorithm to classify service. Next, we discuss the role of state information in improved decision making. Here we contrast the roles of epistemic information (information on uncertain parameters) and aleatoric information (information on an uncertain state). Finally we review recent advances in the theory of reinforcement learning and queueing, as well as, provide discussion on current research challenges.

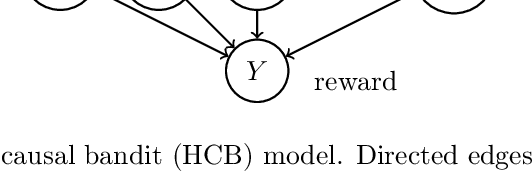
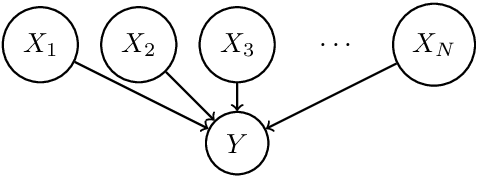
Hierarchical Causal Bandit

Causal bandit is a nascent learning model where an agent sequentially experiments in a causal network of variables, in order to identify the reward-maximizing intervention. Despite the model's wide applicability, existing analytical results are largely restricted to a parallel bandit version where all variables are mutually independent. We introduce in this work the hierarchical causal bandit model as a viable path towards understanding general causal bandits with dependent variables. The core idea is to incorporate a contextual variable that captures the interaction among all variables with direct effects. Using this hierarchical framework, we derive sharp insights on algorithmic design in causal bandits with dependent arms and obtain nearly matching regret bounds in the case of a binary context.

Learner-Private Online Convex Optimization

Online convex optimization is a framework where a learner sequentially queries an external data source in order to arrive at the optimal solution of a convex function. The paradigm has gained significant popularity recently thanks to its scalability in large-scale optimization and machine learning. The repeated interactions, however, expose the learner to privacy risks from eavesdropping adversary that observe the submitted queries. In this paper, we study how to optimally obfuscate the learner's queries in first-order online convex optimization, so that their learned optimal value is provably difficult to estimate for the eavesdropping adversary. We consider two formulations of learner privacy: a Bayesian formulation in which the convex function is drawn randomly, and a minimax formulation in which the function is fixed and the adversary's probability of error is measured with respect to a minimax criterion. We show that, if the learner wants to ensure the probability of accurate prediction by the adversary be kept below $1/L$, then the overhead in query complexity is additive in $L$ in the minimax formulation, but multiplicative in $L$ in the Bayesian formulation. Compared to existing learner-private sequential learning models with binary feedback, our results apply to the significantly richer family of general convex functions with full-gradient feedback. Our proofs are largely enabled by tools from the theory of Dirichlet processes, as well as more sophisticated lines of analysis aimed at measuring the amount of information leakage under a full-gradient oracle.

A Bit Better? Quantifying Information for Bandit Learning

The information ratio offers an approach to assessing the efficacy with which an agent balances between exploration and exploitation. Originally, this was defined to be the ratio between squared expected regret and the mutual information between the environment and action-observation pair, which represents a measure of information gain. Recent work has inspired consideration of alternative information measures, particularly for use in analysis of bandit learning algorithms to arrive at tighter regret bounds. We investigate whether quantification of information via such alternatives can improve the realized performance of information-directed sampling, which aims to minimize the information ratio.

Diffusion Asymptotics for Sequential Experiments

We propose a new diffusion-asymptotic analysis for sequentially randomized experiments. Rather than taking sample size $n$ to infinity while keeping the problem parameters fixed, we let the mean signal level scale to the order $1/\sqrt{n}$ so as to preserve the difficulty of the learning task as $n$ gets large. In this regime, we show that the behavior of a class of methods for sequential experimentation converges to a diffusion limit. This connection enables us to make sharp performance predictions and obtain new insights on the behavior of Thompson sampling. Our diffusion asymptotics also help resolve a discrepancy between the $\Theta(\log(n))$ regret predicted by the fixed-parameter, large-sample asymptotics on the one hand, and the $\Theta(\sqrt{n})$ regret from worst-case, finite-sample analysis on the other, suggesting that it is an appropriate asymptotic regime for understanding practical large-scale sequential experiments.

Query Complexity of Bayesian Private Learning

We study the query complexity of Bayesian Private Learning: a learner wishes to locate a random target within an interval by submitting queries, in the presence of an adversary who observes all of her queries but not the responses. How many queries are necessary and sufficient in order for the learner to accurately estimate the target, while simultaneously concealing the target from the adversary? Our main result is a query complexity lower bound that is tight up to the first order. We show that if the learner wants to estimate the target within an error of $\varepsilon$, while ensuring that no adversary estimator can achieve a constant additive error with probability greater than $1/L$, then the query complexity is on the order of $L\log(1/\varepsilon)$, as $\varepsilon \to 0$. Our result demonstrates that increased privacy, as captured by $L$, comes at the expense of a {multiplicative} increase in query complexity. Our proof method builds on Fano's inequality and a family of proportional-sampling estimators. As an illustration of the method's wider applicability, we generalize the complexity lower bound to settings involving high-dimensional linear query learning and partial adversary observation.

Reinforcement with Fading Memories

We study the effect of imperfect memory on decision making in the context of a stochastic sequential action-reward problem. An agent chooses a sequence of actions which generate discrete rewards at different rates. She is allowed to make new choices at rate $\beta$, while past rewards disappear from her memory at rate $\mu$. We focus on a family of decision rules where the agent makes a new choice by randomly selecting an action with a probability approximately proportional to the amount of past rewards associated with each action in her memory. We provide closed-form formulae for the agent's steady-state choice distribution in the regime where the memory span is large ($\mu \to 0$), and show that the agent's success critically depends on how quickly she updates her choices relative to the speed of memory decay. If $\beta \gg \mu$, the agent almost always chooses the best action, i.e., the one with the highest reward rate. Conversely, if $\beta \ll \mu$, the agent chooses an action with a probability roughly proportional to its reward rate.