Ruiyang Song
Hierarchical Causal Bandit
Mar 07, 2021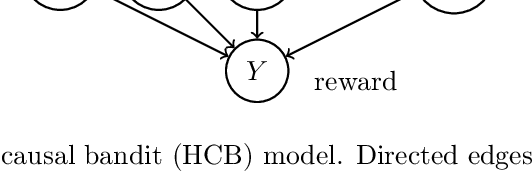
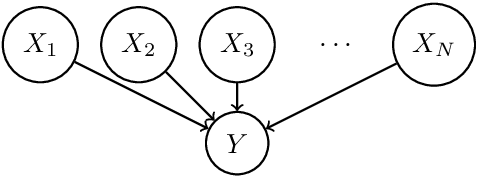
Abstract:Causal bandit is a nascent learning model where an agent sequentially experiments in a causal network of variables, in order to identify the reward-maximizing intervention. Despite the model's wide applicability, existing analytical results are largely restricted to a parallel bandit version where all variables are mutually independent. We introduce in this work the hierarchical causal bandit model as a viable path towards understanding general causal bandits with dependent variables. The core idea is to incorporate a contextual variable that captures the interaction among all variables with direct effects. Using this hierarchical framework, we derive sharp insights on algorithmic design in causal bandits with dependent arms and obtain nearly matching regret bounds in the case of a binary context.
Online Supervised Subspace Tracking
Sep 01, 2015



Abstract:We present a framework for supervised subspace tracking, when there are two time series $x_t$ and $y_t$, one being the high-dimensional predictors and the other being the response variables and the subspace tracking needs to take into consideration of both sequences. It extends the classic online subspace tracking work which can be viewed as tracking of $x_t$ only. Our online sufficient dimensionality reduction (OSDR) is a meta-algorithm that can be applied to various cases including linear regression, logistic regression, multiple linear regression, multinomial logistic regression, support vector machine, the random dot product model and the multi-scale union-of-subspace model. OSDR reduces data-dimensionality on-the-fly with low-computational complexity and it can also handle missing data and dynamic data. OSDR uses an alternating minimization scheme and updates the subspace via gradient descent on the Grassmannian manifold. The subspace update can be performed efficiently utilizing the fact that the Grassmannian gradient with respect to the subspace in many settings is rank-one (or low-rank in certain cases). The optimization problem for OSDR is non-convex and hard to analyze in general; we provide convergence analysis of OSDR in a simple linear regression setting. The good performance of OSDR compared with the conventional unsupervised subspace tracking are demonstrated via numerical examples on simulated and real data.
Sequential Information Guided Sensing
Sep 01, 2015
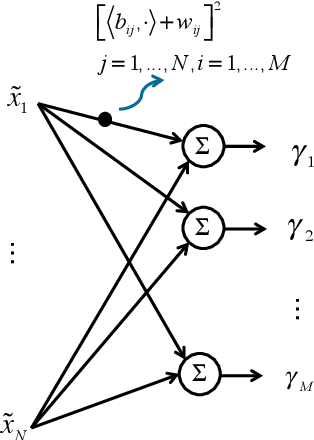
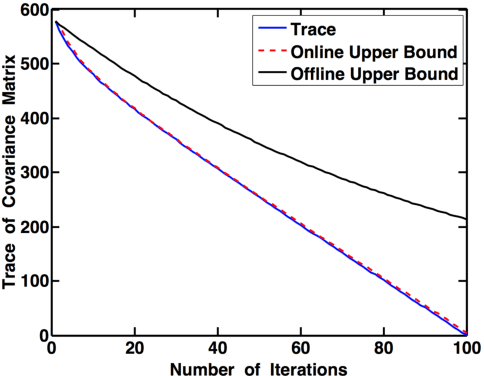
Abstract:We study the value of information in sequential compressed sensing by characterizing the performance of sequential information guided sensing in practical scenarios when information is inaccurate. In particular, we assume the signal distribution is parameterized through Gaussian or Gaussian mixtures with estimated mean and covariance matrices, and we can measure compressively through a noisy linear projection or using one-sparse vectors, i.e., observing one entry of the signal each time. We establish a set of performance bounds for the bias and variance of the signal estimator via posterior mean, by capturing the conditional entropy (which is also related to the size of the uncertainty), and the additional power required due to inaccurate information to reach a desired precision. Based on this, we further study how to estimate covariance based on direct samples or covariance sketching. Numerical examples also demonstrate the superior performance of Info-Greedy Sensing algorithms compared with their random and non-adaptive counterparts.
Sequential Sensing with Model Mismatch
Mar 16, 2015


Abstract:We characterize the performance of sequential information guided sensing, Info-Greedy Sensing, when there is a mismatch between the true signal model and the assumed model, which may be a sample estimate. In particular, we consider a setup where the signal is low-rank Gaussian and the measurements are taken in the directions of eigenvectors of the covariance matrix in a decreasing order of eigenvalues. We establish a set of performance bounds when a mismatched covariance matrix is used, in terms of the gap of signal posterior entropy, as well as the additional amount of power required to achieve the same signal recovery precision. Based on this, we further study how to choose an initialization for Info-Greedy Sensing using the sample covariance matrix, or using an efficient covariance sketching scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge