Hierarchical Causal Bandit
Paper and Code
Mar 07, 2021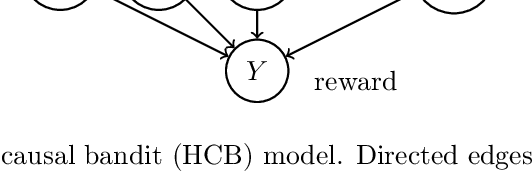
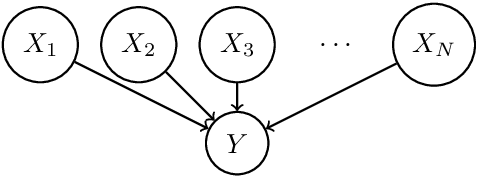
Causal bandit is a nascent learning model where an agent sequentially experiments in a causal network of variables, in order to identify the reward-maximizing intervention. Despite the model's wide applicability, existing analytical results are largely restricted to a parallel bandit version where all variables are mutually independent. We introduce in this work the hierarchical causal bandit model as a viable path towards understanding general causal bandits with dependent variables. The core idea is to incorporate a contextual variable that captures the interaction among all variables with direct effects. Using this hierarchical framework, we derive sharp insights on algorithmic design in causal bandits with dependent arms and obtain nearly matching regret bounds in the case of a binary context.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge