Sequential Information Guided Sensing
Paper and Code
Sep 01, 2015
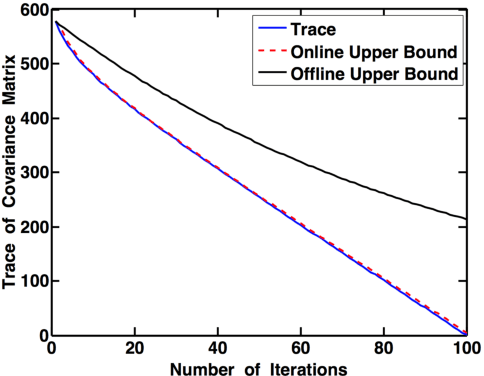
We study the value of information in sequential compressed sensing by characterizing the performance of sequential information guided sensing in practical scenarios when information is inaccurate. In particular, we assume the signal distribution is parameterized through Gaussian or Gaussian mixtures with estimated mean and covariance matrices, and we can measure compressively through a noisy linear projection or using one-sparse vectors, i.e., observing one entry of the signal each time. We establish a set of performance bounds for the bias and variance of the signal estimator via posterior mean, by capturing the conditional entropy (which is also related to the size of the uncertainty), and the additional power required due to inaccurate information to reach a desired precision. Based on this, we further study how to estimate covariance based on direct samples or covariance sketching. Numerical examples also demonstrate the superior performance of Info-Greedy Sensing algorithms compared with their random and non-adaptive counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge