Accelerating Look-ahead in Bayesian Optimization: Multilevel Monte Carlo is All you Need

We leverage multilevel Monte Carlo (MLMC) to improve the performance of multi-step look-ahead Bayesian optimization (BO) methods that involve nested expectations and maximizations. The complexity rate of naive Monte Carlo degrades for nested operations, whereas MLMC is capable of achieving the canonical Monte Carlo convergence rate for this type of problem, independently of dimension and without any smoothness assumptions. Our theoretical study focuses on the approximation improvements for one- and two-step look-ahead acquisition functions, but, as we discuss, the approach is generalizable in various ways, including beyond the context of BO. Findings are verified numerically and the benefits of MLMC for BO are illustrated on several benchmark examples. Code is available here https://github.com/Shangda-Yang/MLMCBO.

Convergence Rates for Stochastic Approximation on a Boundary

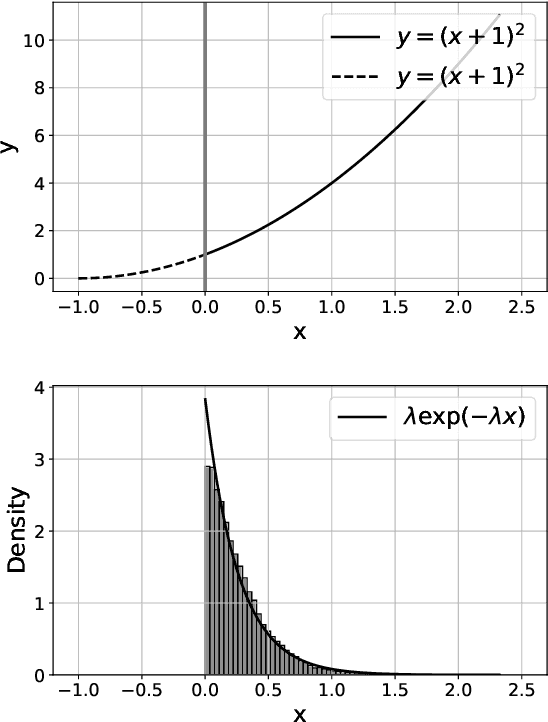
We analyze the behavior of projected stochastic gradient descent focusing on the case where the optimum is on the boundary of the constraint set and the gradient does not vanish at the optimum. Here iterates may in expectation make progress against the objective at each step. When this and an appropriate moment condition on noise holds, we prove that the convergence rate to the optimum of the constrained stochastic gradient descent will be different and typically be faster than the unconstrained stochastic gradient descent algorithm. Our results argue that the concentration around the optimum is exponentially distributed rather than normally distributed, which typically determines the limiting convergence in the unconstrained case. The methods that we develop rely on a geometric ergodicity proof. This extends a result on Markov chains by Hajek (1982) to the area of stochastic approximation algorithms. As examples, we show how the results apply to linear programming and tabular reinforcement learning.

Learning and Information in Stochastic Networks and Queues

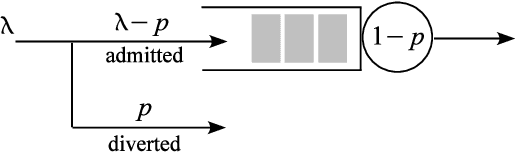
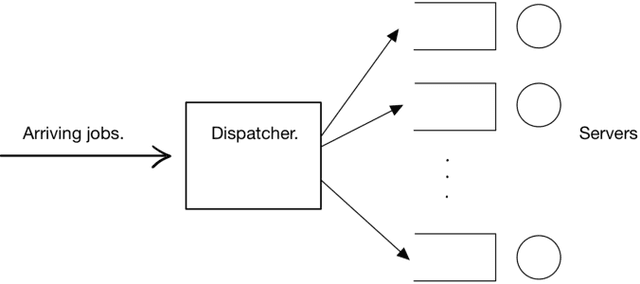
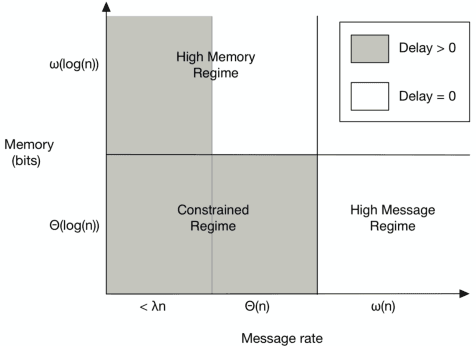
We review the role of information and learning in the stability and optimization of queueing systems. In recent years, techniques from supervised learning, bandit learning and reinforcement learning have been applied to queueing systems supported by increasing role of information in decision making. We present observations and new results that help rationalize the application of these areas to queueing systems. We prove that the MaxWeight and BackPressure policies are an application of Blackwell's Approachability Theorem. This connects queueing theoretic results with adversarial learning. We then discuss the requirements of statistical learning for service parameter estimation. As an example, we show how queue size regret can be bounded when applying a perceptron algorithm to classify service. Next, we discuss the role of state information in improved decision making. Here we contrast the roles of epistemic information (information on uncertain parameters) and aleatoric information (information on an uncertain state). Finally we review recent advances in the theory of reinforcement learning and queueing, as well as, provide discussion on current research challenges.

Reinforcement Learning for Traffic Signal Control: Comparison with Commercial Systems

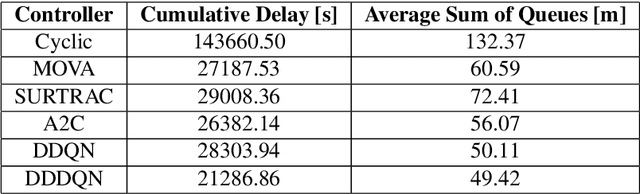
Recently, Intelligent Transportation Systems are leveraging the power of increased sensory coverage and computing power to deliver data-intensive solutions achieving higher levels of performance than traditional systems. Within Traffic Signal Control (TSC), this has allowed the emergence of Machine Learning (ML) based systems. Among this group, Reinforcement Learning (RL) approaches have performed particularly well. Given the lack of industry standards in ML for TSC, literature exploring RL often lacks comparison against commercially available systems and straightforward formulations of how the agents operate. Here we attempt to bridge that gap. We propose three different architectures for TSC RL agents and compare them against the currently used commercial systems MOVA, SurTrac and Cyclic controllers and provide pseudo-code for them. The agents use variations of Deep Q-Learning and Actor Critic, using states and rewards based on queue lengths. Their performance is compared in across different map scenarios with variable demand, assessing them in terms of the global delay and average queue length. We find that the RL-based systems can significantly and consistently achieve lower delays when compared with existing commercial systems.

An Adiabatic Theorem for Policy Tracking with TD-learning

We evaluate the ability of temporal difference learning to track the reward function of a policy as it changes over time. Our results apply a new adiabatic theorem that bounds the mixing time of time-inhomogeneous Markov chains. We derive finite-time bounds for tabular temporal difference learning and $Q$-learning when the policy used for training changes in time. To achieve this, we develop bounds for stochastic approximation under asynchronous adiabatic updates.

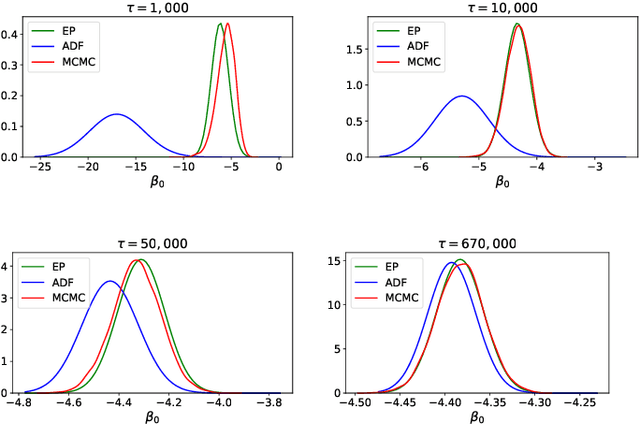
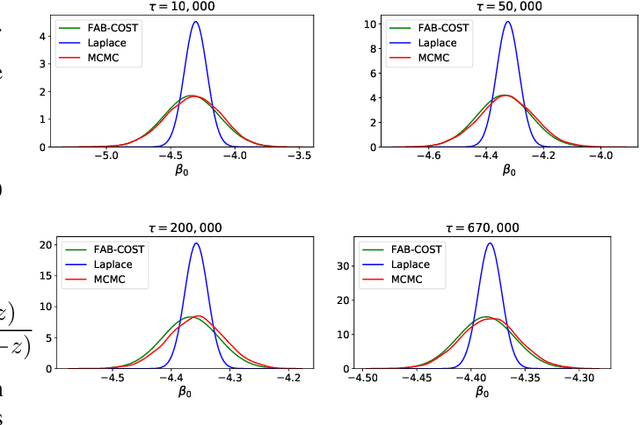
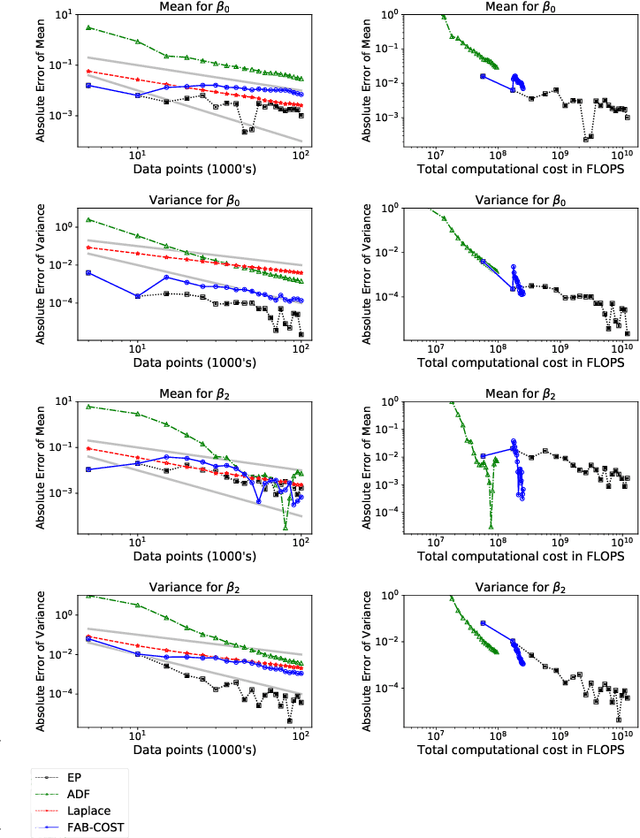
Fast Approximate Bayesian Contextual Cold Start Learning (FAB-COST)

Cold-start is a notoriously difficult problem which can occur in recommendation systems, and arises when there is insufficient information to draw inferences for users or items. To address this challenge, a contextual bandit algorithm -- the Fast Approximate Bayesian Contextual Cold Start Learning algorithm (FAB-COST) -- is proposed, which is designed to provide improved accuracy compared to the traditionally used Laplace approximation in the logistic contextual bandit, while controlling both algorithmic complexity and computational cost. To this end, FAB-COST uses a combination of two moment projection variational methods: Expectation Propagation (EP), which performs well at the cold start, but becomes slow as the amount of data increases; and Assumed Density Filtering (ADF), which has slower growth of computational cost with data size but requires more data to obtain an acceptable level of accuracy. By switching from EP to ADF when the dataset becomes large, it is able to exploit their complementary strengths. The empirical justification for FAB-COST is presented, and systematically compared to other approaches on simulated data. In a benchmark against the Laplace approximation on real data consisting of over $670,000$ impressions from autotrader.co.uk, FAB-COST demonstrates at one point increase of over $16\%$ in user clicks. On the basis of these results, it is argued that FAB-COST is likely to be an attractive approach to cold-start recommendation systems in a variety of contexts.

Regret Analysis of a Markov Policy Gradient Algorithm for Multi-arm Bandits

We consider a policy gradient algorithm applied to a finite-arm bandit problem with Bernoulli rewards. We allow learning rates to depend on the current state of the algorithm, rather than use a deterministic time-decreasing learning rate. The state of the algorithm forms a Markov chain on the probability simplex. We apply Foster-Lyapunov techniques to analyse the stability of this Markov chain. We prove that if learning rates are well chosen then the policy gradient algorithm is a transient Markov chain and the state of the chain converges on the optimal arm with logarithmic or poly-logarithmic regret.

A Short Note on Soft-max and Policy Gradients in Bandits Problems

This is a short communication on a Lyapunov function argument for softmax in bandit problems. There are a number of excellent papers coming out using differential equations for policy gradient algorithms in reinforcement learning \cite{agarwal2019optimality,bhandari2019global,mei2020global}. We give a short argument that gives a regret bound for the soft-max ordinary differential equation for bandit problems. We derive a similar result for a different policy gradient algorithm, again for bandit problems. For this second algorithm, it is possible to prove regret bounds in the stochastic case \cite{DW20}. At the end, we summarize some ideas and issues on deriving stochastic regret bounds for policy gradients.

Adaptive Pricing in Insurance: Generalized Linear Models and Gaussian Process Regression Approaches

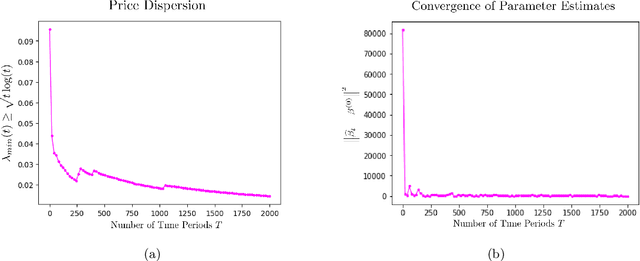
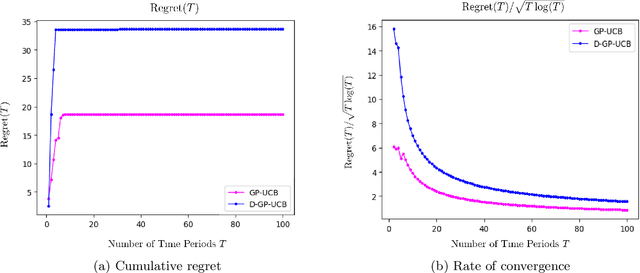
We study the application of dynamic pricing to insurance. We view this as an online revenue management problem where the insurance company looks to set prices to optimize the long-run revenue from selling a new insurance product. We develop two pricing models: an adaptive Generalized Linear Model (GLM) and an adaptive Gaussian Process (GP) regression model. Both balance between exploration, where we choose prices in order to learn the distribution of demands & claims for the insurance product, and exploitation, where we myopically choose the best price from the information gathered so far. The performance of the pricing policies is measured in terms of regret: the expected revenue loss caused by not using the optimal price. As is commonplace in insurance, we model demand and claims by GLMs. In our adaptive GLM design, we use the maximum quasi-likelihood estimation (MQLE) to estimate the unknown parameters. We show that, if prices are chosen with suitably decreasing variability, the MQLE parameters eventually exist and converge to the correct values, which in turn implies that the sequence of chosen prices will also converge to the optimal price. In the adaptive GP regression model, we sample demand and claims from Gaussian Processes and then choose selling prices by the upper confidence bound rule. We also analyze these GLM and GP pricing algorithms with delayed claims. Although similar results exist in other domains, this is among the first works to consider dynamic pricing problems in the field of insurance. We also believe this is the first work to consider Gaussian Process regression in the context of insurance pricing. These initial findings suggest that online machine learning algorithms could be a fruitful area of future investigation and application in insurance.