Accelerating Look-ahead in Bayesian Optimization: Multilevel Monte Carlo is All you Need

We leverage multilevel Monte Carlo (MLMC) to improve the performance of multi-step look-ahead Bayesian optimization (BO) methods that involve nested expectations and maximizations. The complexity rate of naive Monte Carlo degrades for nested operations, whereas MLMC is capable of achieving the canonical Monte Carlo convergence rate for this type of problem, independently of dimension and without any smoothness assumptions. Our theoretical study focuses on the approximation improvements for one- and two-step look-ahead acquisition functions, but, as we discuss, the approach is generalizable in various ways, including beyond the context of BO. Findings are verified numerically and the benefits of MLMC for BO are illustrated on several benchmark examples. Code is available here https://github.com/Shangda-Yang/MLMCBO.

Convergence Rates for Stochastic Approximation on a Boundary

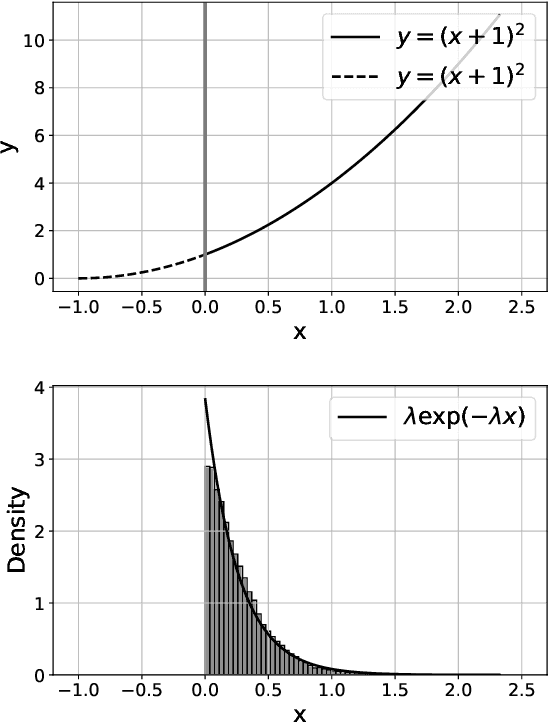
We analyze the behavior of projected stochastic gradient descent focusing on the case where the optimum is on the boundary of the constraint set and the gradient does not vanish at the optimum. Here iterates may in expectation make progress against the objective at each step. When this and an appropriate moment condition on noise holds, we prove that the convergence rate to the optimum of the constrained stochastic gradient descent will be different and typically be faster than the unconstrained stochastic gradient descent algorithm. Our results argue that the concentration around the optimum is exponentially distributed rather than normally distributed, which typically determines the limiting convergence in the unconstrained case. The methods that we develop rely on a geometric ergodicity proof. This extends a result on Markov chains by Hajek (1982) to the area of stochastic approximation algorithms. As examples, we show how the results apply to linear programming and tabular reinforcement learning.