Accelerating Look-ahead in Bayesian Optimization: Multilevel Monte Carlo is All you Need

We leverage multilevel Monte Carlo (MLMC) to improve the performance of multi-step look-ahead Bayesian optimization (BO) methods that involve nested expectations and maximizations. The complexity rate of naive Monte Carlo degrades for nested operations, whereas MLMC is capable of achieving the canonical Monte Carlo convergence rate for this type of problem, independently of dimension and without any smoothness assumptions. Our theoretical study focuses on the approximation improvements for one- and two-step look-ahead acquisition functions, but, as we discuss, the approach is generalizable in various ways, including beyond the context of BO. Findings are verified numerically and the benefits of MLMC for BO are illustrated on several benchmark examples. Code is available here https://github.com/Shangda-Yang/MLMCBO.

Neural Stress Fields for Reduced-order Elastoplasticity and Fracture

We propose a hybrid neural network and physics framework for reduced-order modeling of elastoplasticity and fracture. State-of-the-art scientific computing models like the Material Point Method (MPM) faithfully simulate large-deformation elastoplasticity and fracture mechanics. However, their long runtime and large memory consumption render them unsuitable for applications constrained by computation time and memory usage, e.g., virtual reality. To overcome these barriers, we propose a reduced-order framework. Our key innovation is training a low-dimensional manifold for the Kirchhoff stress field via an implicit neural representation. This low-dimensional neural stress field (NSF) enables efficient evaluations of stress values and, correspondingly, internal forces at arbitrary spatial locations. In addition, we also train neural deformation and affine fields to build low-dimensional manifolds for the deformation and affine momentum fields. These neural stress, deformation, and affine fields share the same low-dimensional latent space, which uniquely embeds the high-dimensional simulation state. After training, we run new simulations by evolving in this single latent space, which drastically reduces the computation time and memory consumption. Our general continuum-mechanics-based reduced-order framework is applicable to any phenomena governed by the elastodynamics equation. To showcase the versatility of our framework, we simulate a wide range of material behaviors, including elastica, sand, metal, non-Newtonian fluids, fracture, contact, and collision. We demonstrate dimension reduction by up to 100,000X and time savings by up to 10X.

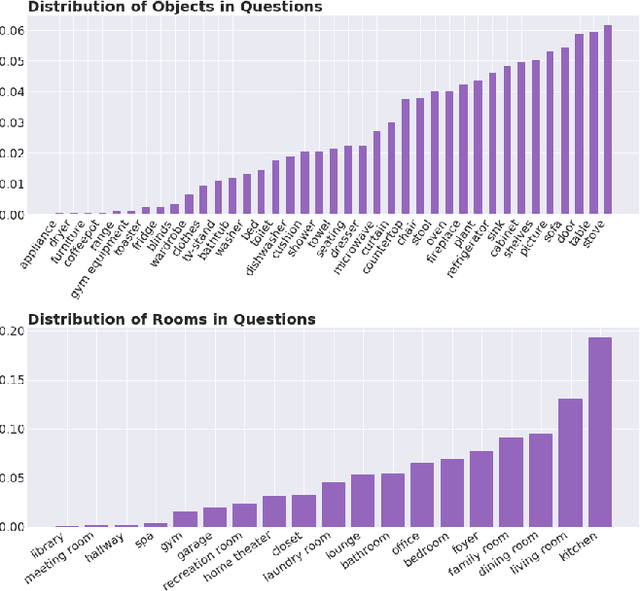
Learning a Visually Grounded Memory Assistant

We introduce a novel interface for large scale collection of human memory and assistance. Using the 3D Matterport simulator we create a realistic indoor environments in which we have people perform specific embodied memory tasks that mimic household daily activities. This interface was then deployed on Amazon Mechanical Turk allowing us to test and record human memory, navigation and needs for assistance at a large scale that was previously impossible. Using the interface we collect the `The Visually Grounded Memory Assistant Dataset' which is aimed at developing our understanding of (1) the information people encode during navigation of 3D environments and (2) conditions under which people ask for memory assistance. Additionally we experiment with with predicting when people will ask for assistance using models trained on hand-selected visual and semantic features. This provides an opportunity to build stronger ties between the machine-learning and cognitive-science communities through learned models of human perception, memory, and cognition.

CROM: Continuous Reduced-Order Modeling of PDEs Using Implicit Neural Representations

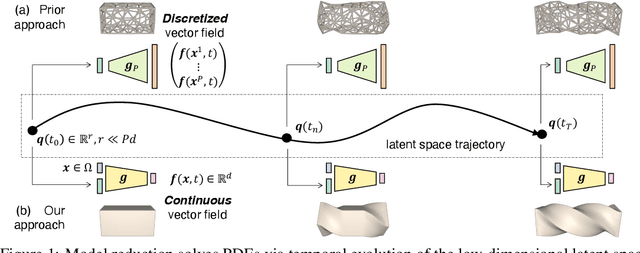
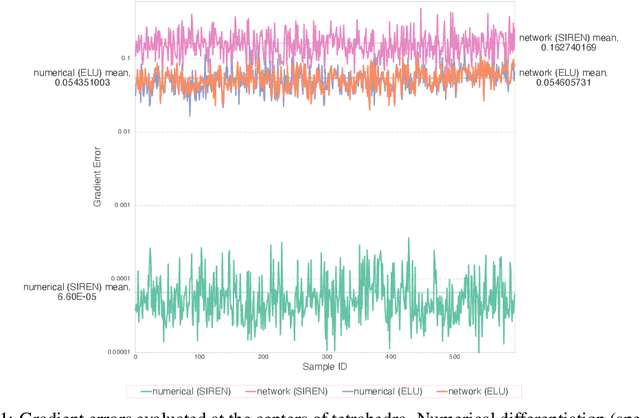
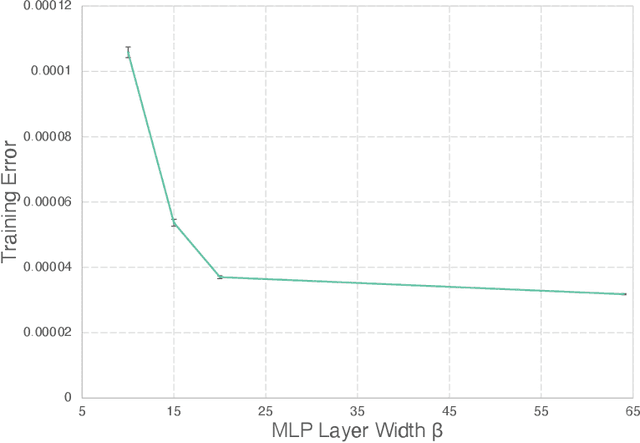
The excessive runtime of high-fidelity partial differential equation (PDE) solvers makes them unsuitable for time-critical applications. We propose to accelerate PDE solvers using reduced-order modeling (ROM). Whereas prior ROM approaches reduce the dimensionality of discretized vector fields, our continuous reduced-order modeling (CROM) approach builds a smooth, low-dimensional manifold of the continuous vector fields themselves, not their discretization. We represent this reduced manifold using neural fields, relying on their continuous and differentiable nature to efficiently solve the PDEs. CROM may train on any and all available numerical solutions of the continuous system, even when they are obtained using diverse methods or discretizations. After the low-dimensional manifolds are built, solving PDEs requires significantly less computational resources. Since CROM is discretization-agnostic, CROM-based PDE solvers may optimally adapt discretization resolution over time to economize computation. We validate our approach on an extensive range of PDEs with training data from voxel grids, meshes, and point clouds. Large-scale experiments demonstrate that our approach obtains speed, memory, and accuracy advantages over prior ROM approaches while gaining 109$\times$ wall-clock speedup over full-order models on CPUs and 89$\times$ speedup on GPUs.

Model reduction for the material point method via learning the deformation map and its spatial-temporal gradients

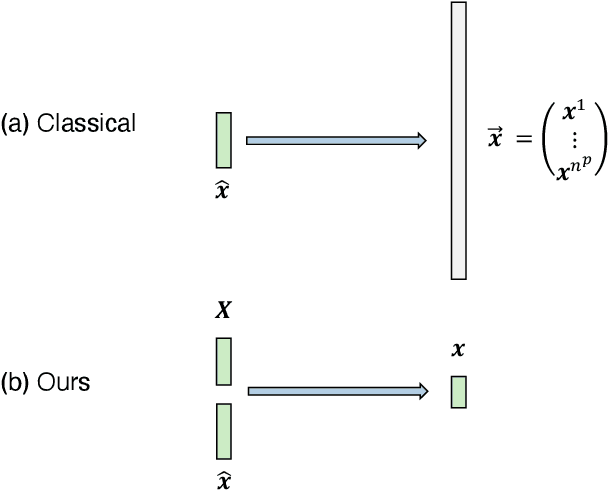
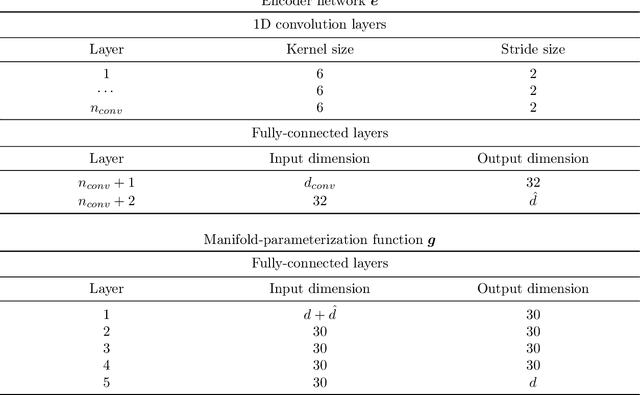
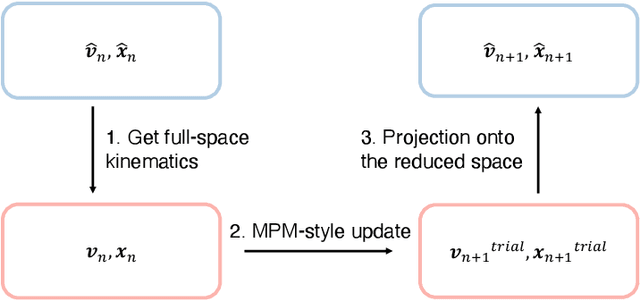
This work proposes a model-reduction approach for the material point method on nonlinear manifolds. The technique approximates the $\textit{kinematics}$ by approximating the deformation map in a manner that restricts deformation trajectories to reside on a low-dimensional manifold expressed from the extrinsic view via a parameterization function. By explicitly approximating the deformation map and its spatial-temporal gradients, the deformation gradient and the velocity can be computed simply by differentiating the associated parameterization function. Unlike classical model reduction techniques that build a subspace for a finite number of degrees of freedom, the proposed method approximates the entire deformation map with infinite degrees of freedom. Therefore, the technique supports resolution changes in the reduced simulation, attaining the challenging task of zero-shot super-resolution by generating material points unseen in the training data. The ability to generate material points also allows for adaptive quadrature rules for stress update. A family of projection methods is devised to generate $\textit{dynamics}$, i.e., at every time step, the methods perform three steps: (1) generate quadratures in the full space from the reduced space, (2) compute position and velocity updates in the full space, and (3) perform a least-squares projection of the updated position and velocity onto the low-dimensional manifold and its tangent space. Computational speedup is achieved via hyper-reduction, i.e., only a subset of the original material points are needed for dynamics update. Large-scale numerical examples with millions of material points illustrate the method's ability to gain an order-of-magnitude computational-cost saving -- indeed $\textit{real-time simulations}$ in some cases -- with negligible errors.

Optimal Assistance for Object-Rearrangement Tasks in Augmented Reality

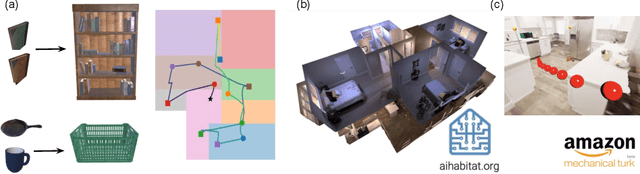
Augmented-reality (AR) glasses that will have access to onboard sensors and an ability to display relevant information to the user present an opportunity to provide user assistance in quotidian tasks. Many such tasks can be characterized as object-rearrangement tasks. We introduce a novel framework for computing and displaying AR assistance that consists of (1) associating an optimal action sequence with the policy of an embodied agent and (2) presenting this sequence to the user as suggestions in the AR system's heads-up display. The embodied agent comprises a "hybrid" between the AR system and the user, with the AR system's observation space (i.e., sensors) and the user's action space (i.e., task-execution actions); its policy is learned by minimizing the task-completion time. In this initial study, we assume that the AR system's observations include the environment's map and localization of the objects and the user. These choices allow us to formalize the problem of computing AR assistance for any object-rearrangement task as a planning problem, specifically as a capacitated vehicle-routing problem. Further, we introduce a novel AR simulator that can enable web-based evaluation of AR-like assistance and associated at-scale data collection via the Habitat simulator for embodied artificial intelligence. Finally, we perform a study that evaluates user response to the proposed form of AR assistance on a specific quotidian object-rearrangement task, house cleaning, using our proposed AR simulator on mechanical turk. In particular, we study the effect of the proposed AR assistance on users' task performance and sense of agency over a range of task difficulties. Our results indicate that providing users with such assistance improves their overall performance and while users report a negative impact to their agency, they may still prefer the proposed assistance to having no assistance at all.

The ROMES method for statistical modeling of reduced-order-model error

This work presents a technique for statistically modeling errors introduced by reduced-order models. The method employs Gaussian-process regression to construct a mapping from a small number of computationally inexpensive `error indicators' to a distribution over the true error. The variance of this distribution can be interpreted as the (epistemic) uncertainty introduced by the reduced-order model. To model normed errors, the method employs existing rigorous error bounds and residual norms as indicators; numerical experiments show that the method leads to a near-optimal expected effectivity in contrast to typical error bounds. To model errors in general outputs, the method uses dual-weighted residuals---which are amenable to uncertainty control---as indicators. Experiments illustrate that correcting the reduced-order-model output with this surrogate can improve prediction accuracy by an order of magnitude; this contrasts with existing `multifidelity correction' approaches, which often fail for reduced-order models and suffer from the curse of dimensionality. The proposed error surrogates also lead to a notion of `probabilistic rigor', i.e., the surrogate bounds the error with specified probability.