CROM: Continuous Reduced-Order Modeling of PDEs Using Implicit Neural Representations

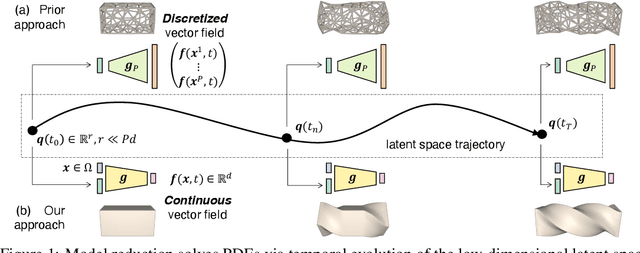
The excessive runtime of high-fidelity partial differential equation (PDE) solvers makes them unsuitable for time-critical applications. We propose to accelerate PDE solvers using reduced-order modeling (ROM). Whereas prior ROM approaches reduce the dimensionality of discretized vector fields, our continuous reduced-order modeling (CROM) approach builds a smooth, low-dimensional manifold of the continuous vector fields themselves, not their discretization. We represent this reduced manifold using neural fields, relying on their continuous and differentiable nature to efficiently solve the PDEs. CROM may train on any and all available numerical solutions of the continuous system, even when they are obtained using diverse methods or discretizations. After the low-dimensional manifolds are built, solving PDEs requires significantly less computational resources. Since CROM is discretization-agnostic, CROM-based PDE solvers may optimally adapt discretization resolution over time to economize computation. We validate our approach on an extensive range of PDEs with training data from voxel grids, meshes, and point clouds. Large-scale experiments demonstrate that our approach obtains speed, memory, and accuracy advantages over prior ROM approaches while gaining 109$\times$ wall-clock speedup over full-order models on CPUs and 89$\times$ speedup on GPUs.

Model reduction for the material point method via learning the deformation map and its spatial-temporal gradients

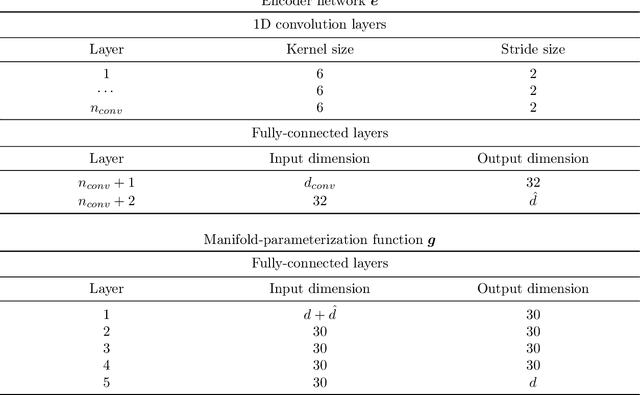
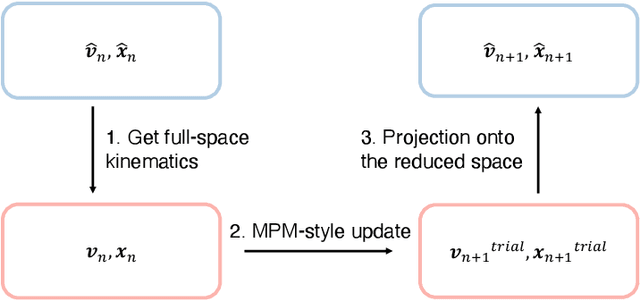
This work proposes a model-reduction approach for the material point method on nonlinear manifolds. The technique approximates the $\textit{kinematics}$ by approximating the deformation map in a manner that restricts deformation trajectories to reside on a low-dimensional manifold expressed from the extrinsic view via a parameterization function. By explicitly approximating the deformation map and its spatial-temporal gradients, the deformation gradient and the velocity can be computed simply by differentiating the associated parameterization function. Unlike classical model reduction techniques that build a subspace for a finite number of degrees of freedom, the proposed method approximates the entire deformation map with infinite degrees of freedom. Therefore, the technique supports resolution changes in the reduced simulation, attaining the challenging task of zero-shot super-resolution by generating material points unseen in the training data. The ability to generate material points also allows for adaptive quadrature rules for stress update. A family of projection methods is devised to generate $\textit{dynamics}$, i.e., at every time step, the methods perform three steps: (1) generate quadratures in the full space from the reduced space, (2) compute position and velocity updates in the full space, and (3) perform a least-squares projection of the updated position and velocity onto the low-dimensional manifold and its tangent space. Computational speedup is achieved via hyper-reduction, i.e., only a subset of the original material points are needed for dynamics update. Large-scale numerical examples with millions of material points illustrate the method's ability to gain an order-of-magnitude computational-cost saving -- indeed $\textit{real-time simulations}$ in some cases -- with negligible errors.