Automated Discovery of Continuous Dynamics from Videos

Dynamical systems form the foundation of scientific discovery, traditionally modeled with predefined state variables such as the angle and angular velocity, and differential equations such as the equation of motion for a single pendulum. We propose an approach to discover a set of state variables that preserve the smoothness of the system dynamics and to construct a vector field representing the system's dynamics equation, automatically from video streams without prior physical knowledge. The prominence and effectiveness of the proposed approach are demonstrated through both quantitative and qualitative analyses of various dynamical systems, including the prediction of characteristic frequencies and the identification of chaotic and limit cycle behaviors. This shows the potential of our approach to assist human scientists in scientific discovery.

CROM: Continuous Reduced-Order Modeling of PDEs Using Implicit Neural Representations

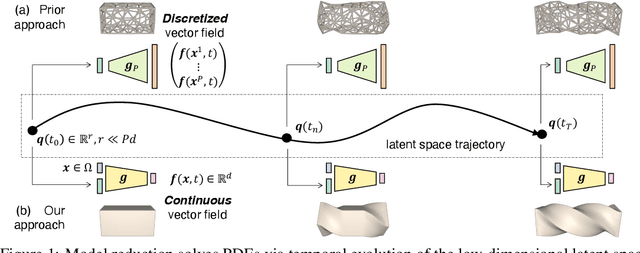
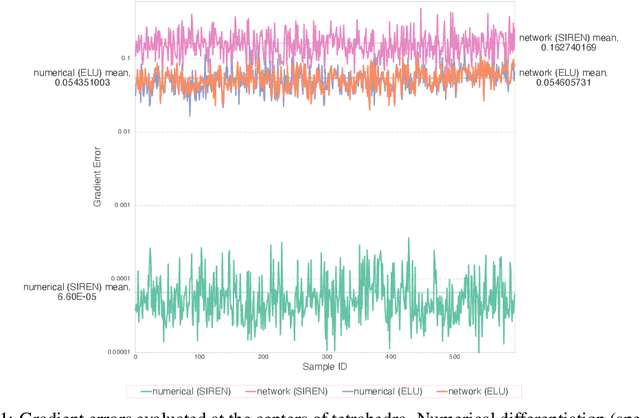
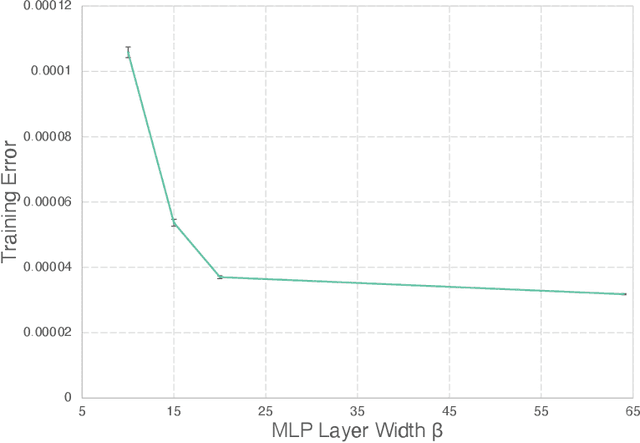
The excessive runtime of high-fidelity partial differential equation (PDE) solvers makes them unsuitable for time-critical applications. We propose to accelerate PDE solvers using reduced-order modeling (ROM). Whereas prior ROM approaches reduce the dimensionality of discretized vector fields, our continuous reduced-order modeling (CROM) approach builds a smooth, low-dimensional manifold of the continuous vector fields themselves, not their discretization. We represent this reduced manifold using neural fields, relying on their continuous and differentiable nature to efficiently solve the PDEs. CROM may train on any and all available numerical solutions of the continuous system, even when they are obtained using diverse methods or discretizations. After the low-dimensional manifolds are built, solving PDEs requires significantly less computational resources. Since CROM is discretization-agnostic, CROM-based PDE solvers may optimally adapt discretization resolution over time to economize computation. We validate our approach on an extensive range of PDEs with training data from voxel grids, meshes, and point clouds. Large-scale experiments demonstrate that our approach obtains speed, memory, and accuracy advantages over prior ROM approaches while gaining 109$\times$ wall-clock speedup over full-order models on CPUs and 89$\times$ speedup on GPUs.

Learning Temporally Invariant and Localizable Features via Data Augmentation for Video Recognition

Deep-Learning-based video recognition has shown promising improvements along with the development of large-scale datasets and spatiotemporal network architectures. In image recognition, learning spatially invariant features is a key factor in improving recognition performance and robustness. Data augmentation based on visual inductive priors, such as cropping, flipping, rotating, or photometric jittering, is a representative approach to achieve these features. Recent state-of-the-art recognition solutions have relied on modern data augmentation strategies that exploit a mixture of augmentation operations. In this study, we extend these strategies to the temporal dimension for videos to learn temporally invariant or temporally localizable features to cover temporal perturbations or complex actions in videos. Based on our novel temporal data augmentation algorithms, video recognition performances are improved using only a limited amount of training data compared to the spatial-only data augmentation algorithms, including the 1st Visual Inductive Priors (VIPriors) for data-efficient action recognition challenge. Furthermore, learned features are temporally localizable that cannot be achieved using spatial augmentation algorithms. Our source code is available at https://github.com/taeoh-kim/temporal_data_augmentation.