Automated Discovery of Continuous Dynamics from Videos

Dynamical systems form the foundation of scientific discovery, traditionally modeled with predefined state variables such as the angle and angular velocity, and differential equations such as the equation of motion for a single pendulum. We propose an approach to discover a set of state variables that preserve the smoothness of the system dynamics and to construct a vector field representing the system's dynamics equation, automatically from video streams without prior physical knowledge. The prominence and effectiveness of the proposed approach are demonstrated through both quantitative and qualitative analyses of various dynamical systems, including the prediction of characteristic frequencies and the identification of chaotic and limit cycle behaviors. This shows the potential of our approach to assist human scientists in scientific discovery.

Discovering State Variables Hidden in Experimental Data

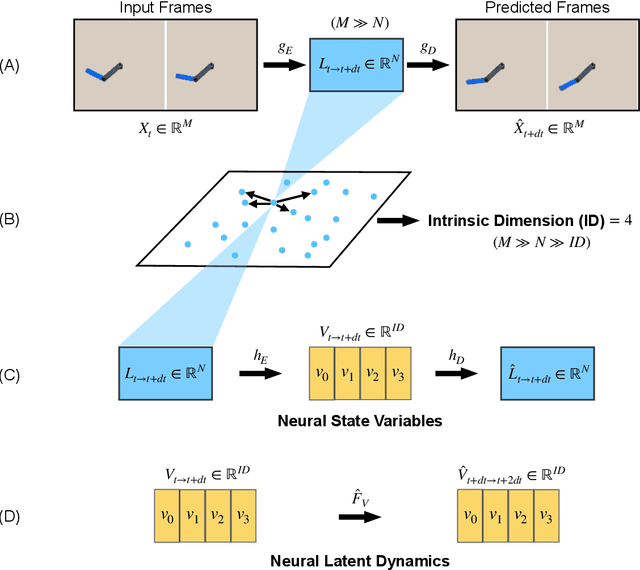
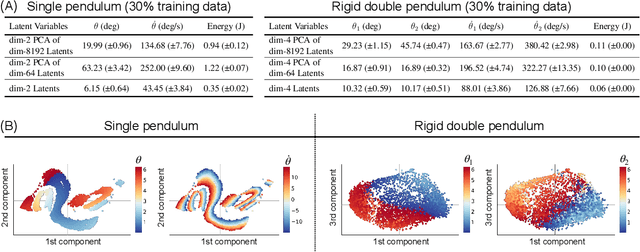
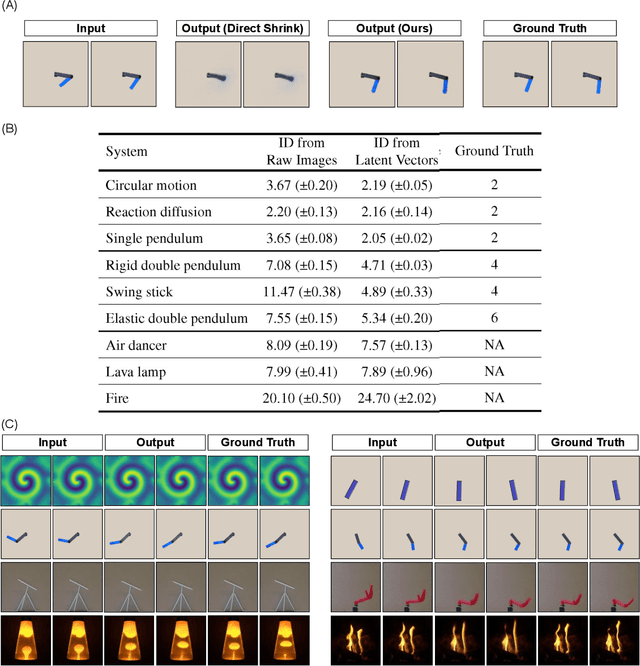
All physical laws are described as relationships between state variables that give a complete and non-redundant description of the relevant system dynamics. However, despite the prevalence of computing power and AI, the process of identifying the hidden state variables themselves has resisted automation. Most data-driven methods for modeling physical phenomena still assume that observed data streams already correspond to relevant state variables. A key challenge is to identify the possible sets of state variables from scratch, given only high-dimensional observational data. Here we propose a new principle for determining how many state variables an observed system is likely to have, and what these variables might be, directly from video streams. We demonstrate the effectiveness of this approach using video recordings of a variety of physical dynamical systems, ranging from elastic double pendulums to fire flames. Without any prior knowledge of the underlying physics, our algorithm discovers the intrinsic dimension of the observed dynamics and identifies candidate sets of state variables. We suggest that this approach could help catalyze the understanding, prediction and control of increasingly complex systems. Project website is at: https://www.cs.columbia.edu/~bchen/neural-state-variables

A Physics-Informed Deep Learning Paradigm for Traffic State Estimation and Fundamental Diagram Discovery

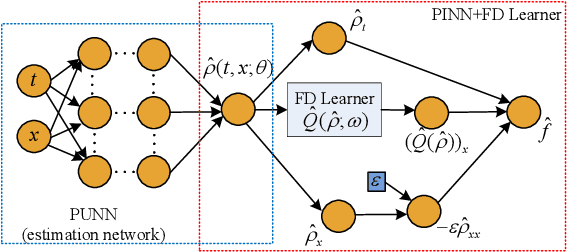
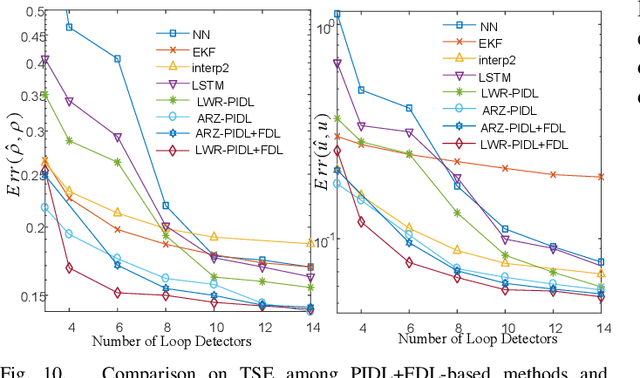
Traffic state estimation (TSE) bifurcates into two main categories, model-driven and data-driven (e.g., machine learning, ML) approaches, while each suffers from either deficient physics or small data. To mitigate these limitations, recent studies introduced hybrid methods, such as physics-informed deep learning (PIDL), which contains both model-driven and data-driven components. This paper contributes an improved paradigm, called physics-informed deep learning with a fundamental diagram learner (PIDL+FDL), which integrates ML terms into the model-driven component to learn a functional form of a fundamental diagram (FD), i.e., a mapping from traffic density to flow or velocity. The proposed PIDL+FDL has the advantages of performing the TSE learning, model parameter discovery, and FD discovery simultaneously. This paper focuses on highway TSE with observed data from loop detectors, using traffic density or velocity as traffic variables. We demonstrate the use of PIDL+FDL to solve popular first-order and second-order traffic flow models and reconstruct the FD relation as well as model parameters that are outside the FD term. We then evaluate the PIDL+FDL-based TSE using the Next Generation SIMulation (NGSIM) dataset. The experimental results show the superiority of the PIDL+FDL in terms of improved estimation accuracy and data efficiency over advanced baseline TSE methods, and additionally, the capacity to properly learn the unknown underlying FD relation.

Physics-Informed Deep Learning for Traffic State Estimation

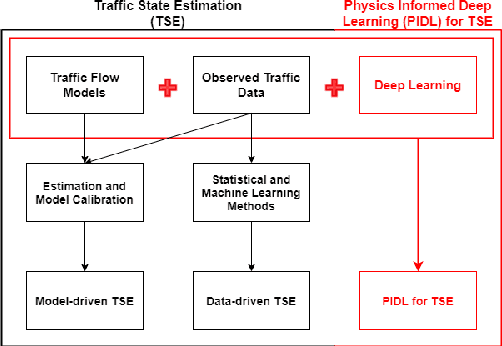
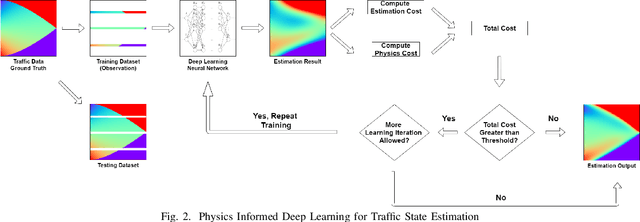
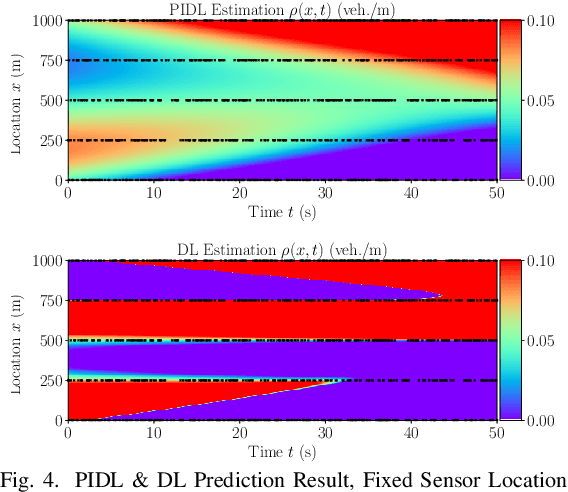
Traffic state estimation (TSE), which reconstructs the traffic variables (e.g., density) on road segments using partially observed data, plays an important role on efficient traffic control and operation that intelligent transportation systems (ITS) need to provide to people. Over decades, TSE approaches bifurcate into two main categories, model-driven approaches and data-driven approaches. However, each of them has limitations: the former highly relies on existing physical traffic flow models, such as Lighthill-Whitham-Richards (LWR) models, which may only capture limited dynamics of real-world traffic, resulting in low-quality estimation, while the latter requires massive data in order to perform accurate and generalizable estimation. To mitigate the limitations, this paper introduces a physics-informed deep learning (PIDL) framework to efficiently conduct high-quality TSE with small amounts of observed data. PIDL contains both model-driven and data-driven components, making possible the integration of the strong points of both approaches while overcoming the shortcomings of either. This paper focuses on highway TSE with observed data from loop detectors, using traffic density as the traffic variables. We demonstrate the use of PIDL to solve (with data from loop detectors) two popular physical traffic flow models, i.e., Greenshields-based LWR and three-parameter-based LWR, and discover the model parameters. We then evaluate the PIDL-based highway TSE using the Next Generation SIMulation (NGSIM) dataset. The experimental results show the advantages of the PIDL-based approach in terms of estimation accuracy and data efficiency over advanced baseline TSE methods.