Factorized Neural Implicit DMD for Parametric Dynamics

A data-driven, model-free approach to modeling the temporal evolution of physical systems mitigates the need for explicit knowledge of the governing equations. Even when physical priors such as partial differential equations are available, such systems often reside in high-dimensional state spaces and exhibit nonlinear dynamics, making traditional numerical solvers computationally expensive and ill-suited for real-time analysis and control. Consider the problem of learning a parametric flow of a dynamical system: with an initial field and a set of physical parameters, we aim to predict the system's evolution over time in a way that supports long-horizon rollouts, generalization to unseen parameters, and spectral analysis. We propose a physics-coded neural field parameterization of the Koopman operator's spectral decomposition. Unlike a physics-constrained neural field, which fits a single solution surface, and neural operators, which directly approximate the solution operator at fixed time horizons, our model learns a factorized flow operator that decouples spatial modes and temporal evolution. This structure exposes underlying eigenvalues, modes, and stability of the underlying physical process to enable stable long-term rollouts, interpolation across parameter spaces, and spectral analysis. We demonstrate the efficacy of our method on a range of dynamics problems, showcasing its ability to accurately predict complex spatiotemporal phenomena while providing insights into the system's dynamic behavior.

Variational Green's Functions for Volumetric PDEs

Green's functions characterize the fundamental solutions of partial differential equations; they are essential for tasks ranging from shape analysis to physical simulation, yet they remain computationally prohibitive to evaluate on arbitrary geometric discretizations. We present Variational Green's Function (VGF), a method that learns a smooth, differentiable representation of the Green's function for linear self-adjoint PDE operators, including the Poisson, the screened Poisson, and the biharmonic equations. To resolve the sharp singularities characteristic of the Green's functions, our method decomposes the Green's function into an analytic free-space component, and a learned corrector component. Our method leverages a variational foundation to impose Neumann boundary conditions naturally, and imposes Dirichlet boundary conditions via a projective layer on the output of the neural field. The resulting Green's functions are fast to evaluate, differentiable with respect to source application, and can be conditioned on other signals parameterizing our geometry.

Neural Stress Fields for Reduced-order Elastoplasticity and Fracture

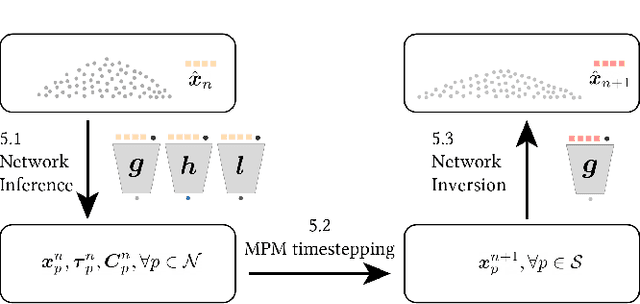
We propose a hybrid neural network and physics framework for reduced-order modeling of elastoplasticity and fracture. State-of-the-art scientific computing models like the Material Point Method (MPM) faithfully simulate large-deformation elastoplasticity and fracture mechanics. However, their long runtime and large memory consumption render them unsuitable for applications constrained by computation time and memory usage, e.g., virtual reality. To overcome these barriers, we propose a reduced-order framework. Our key innovation is training a low-dimensional manifold for the Kirchhoff stress field via an implicit neural representation. This low-dimensional neural stress field (NSF) enables efficient evaluations of stress values and, correspondingly, internal forces at arbitrary spatial locations. In addition, we also train neural deformation and affine fields to build low-dimensional manifolds for the deformation and affine momentum fields. These neural stress, deformation, and affine fields share the same low-dimensional latent space, which uniquely embeds the high-dimensional simulation state. After training, we run new simulations by evolving in this single latent space, which drastically reduces the computation time and memory consumption. Our general continuum-mechanics-based reduced-order framework is applicable to any phenomena governed by the elastodynamics equation. To showcase the versatility of our framework, we simulate a wide range of material behaviors, including elastica, sand, metal, non-Newtonian fluids, fracture, contact, and collision. We demonstrate dimension reduction by up to 100,000X and time savings by up to 10X.

Implicit Neural Spatial Representations for Time-dependent PDEs

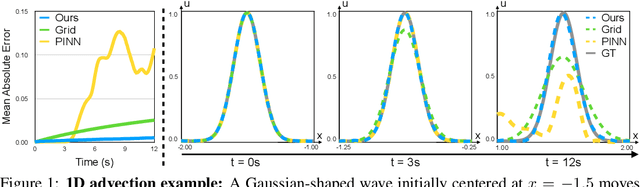
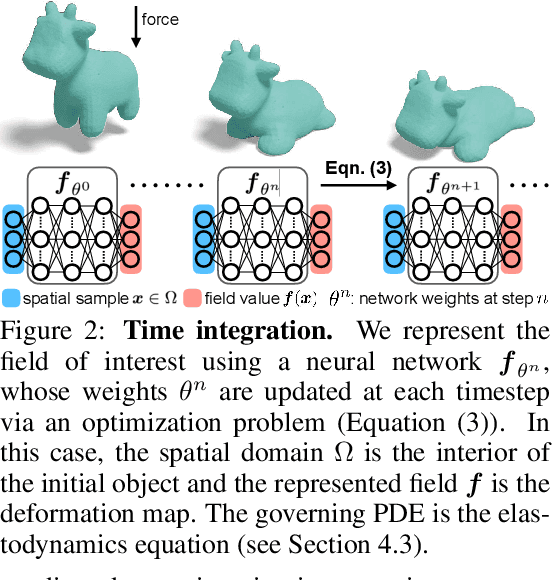
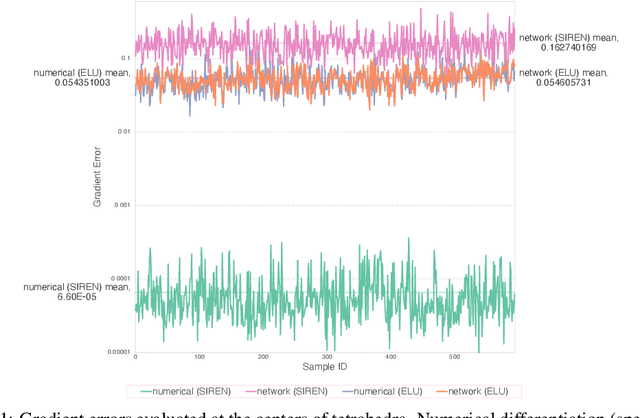
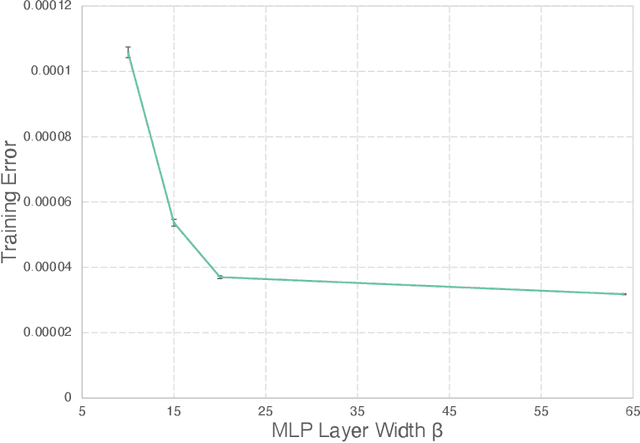
Numerically solving partial differential equations (PDEs) often entails spatial and temporal discretizations. Traditional methods (e.g., finite difference, finite element, smoothed-particle hydrodynamics) frequently adopt explicit spatial discretizations, such as grids, meshes, and point clouds, where each degree-of-freedom corresponds to a location in space. While these explicit spatial correspondences are intuitive to model and understand, these representations are not necessarily optimal for accuracy, memory-usage, or adaptivity. In this work, we explore implicit neural representation as an alternative spatial discretization, where spatial information is implicitly stored in the neural network weights. With implicit neural spatial representation, PDE-constrained time-stepping translates into updating neural network weights, which naturally integrates with commonly adopted optimization time integrators. We validate our approach on a variety of classic PDEs with examples involving large elastic deformations, turbulent fluids, and multiscale phenomena. While slower to compute than traditional representations, our approach exhibits higher accuracy, lower memory consumption, and dynamically adaptive allocation of degrees of freedom without complex remeshing.

CROM: Continuous Reduced-Order Modeling of PDEs Using Implicit Neural Representations

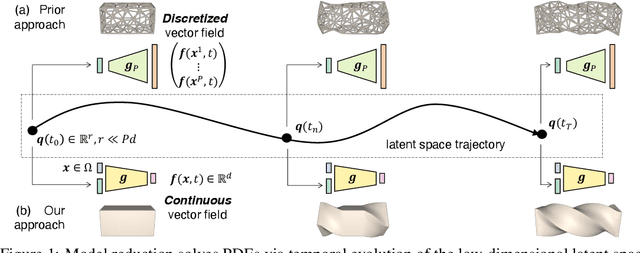
The excessive runtime of high-fidelity partial differential equation (PDE) solvers makes them unsuitable for time-critical applications. We propose to accelerate PDE solvers using reduced-order modeling (ROM). Whereas prior ROM approaches reduce the dimensionality of discretized vector fields, our continuous reduced-order modeling (CROM) approach builds a smooth, low-dimensional manifold of the continuous vector fields themselves, not their discretization. We represent this reduced manifold using neural fields, relying on their continuous and differentiable nature to efficiently solve the PDEs. CROM may train on any and all available numerical solutions of the continuous system, even when they are obtained using diverse methods or discretizations. After the low-dimensional manifolds are built, solving PDEs requires significantly less computational resources. Since CROM is discretization-agnostic, CROM-based PDE solvers may optimally adapt discretization resolution over time to economize computation. We validate our approach on an extensive range of PDEs with training data from voxel grids, meshes, and point clouds. Large-scale experiments demonstrate that our approach obtains speed, memory, and accuracy advantages over prior ROM approaches while gaining 109$\times$ wall-clock speedup over full-order models on CPUs and 89$\times$ speedup on GPUs.

Model reduction for the material point method via learning the deformation map and its spatial-temporal gradients

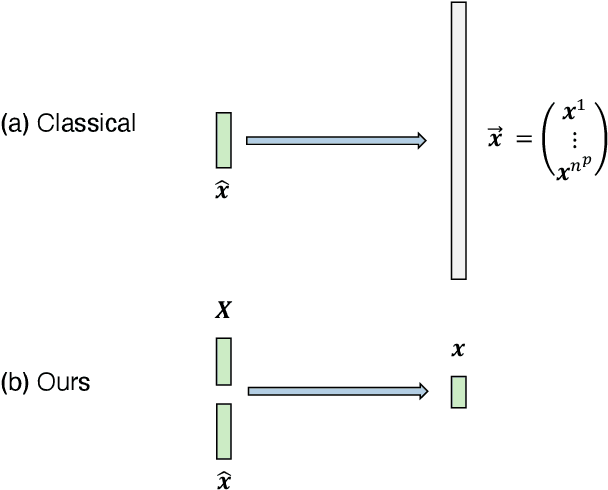
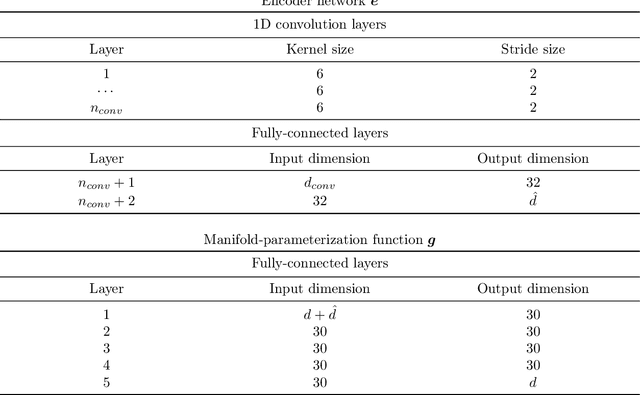
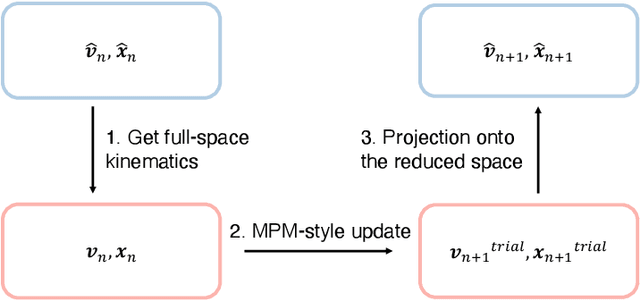
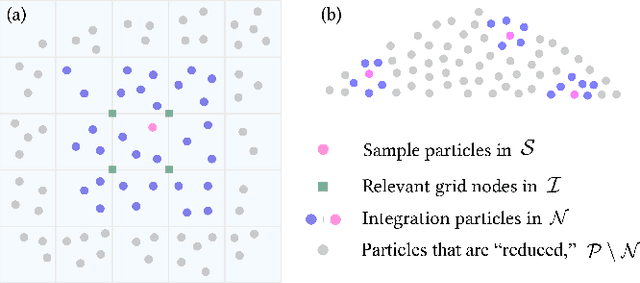
This work proposes a model-reduction approach for the material point method on nonlinear manifolds. The technique approximates the $\textit{kinematics}$ by approximating the deformation map in a manner that restricts deformation trajectories to reside on a low-dimensional manifold expressed from the extrinsic view via a parameterization function. By explicitly approximating the deformation map and its spatial-temporal gradients, the deformation gradient and the velocity can be computed simply by differentiating the associated parameterization function. Unlike classical model reduction techniques that build a subspace for a finite number of degrees of freedom, the proposed method approximates the entire deformation map with infinite degrees of freedom. Therefore, the technique supports resolution changes in the reduced simulation, attaining the challenging task of zero-shot super-resolution by generating material points unseen in the training data. The ability to generate material points also allows for adaptive quadrature rules for stress update. A family of projection methods is devised to generate $\textit{dynamics}$, i.e., at every time step, the methods perform three steps: (1) generate quadratures in the full space from the reduced space, (2) compute position and velocity updates in the full space, and (3) perform a least-squares projection of the updated position and velocity onto the low-dimensional manifold and its tangent space. Computational speedup is achieved via hyper-reduction, i.e., only a subset of the original material points are needed for dynamics update. Large-scale numerical examples with millions of material points illustrate the method's ability to gain an order-of-magnitude computational-cost saving -- indeed $\textit{real-time simulations}$ in some cases -- with negligible errors.

Can one hear the shape of a neural network?: Snooping the GPU via Magnetic Side Channel

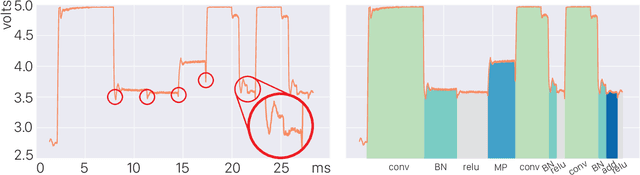
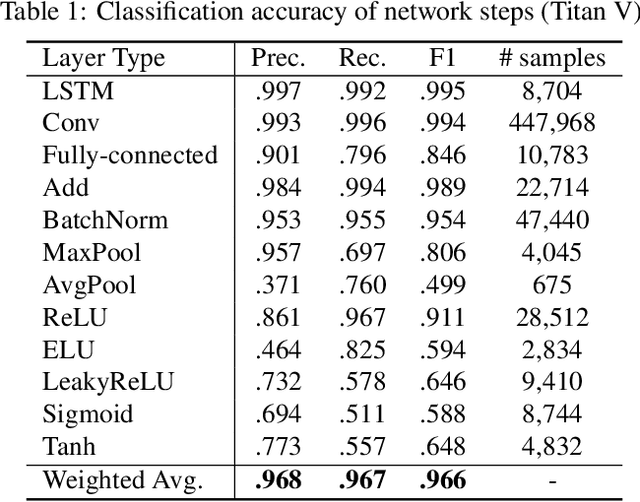
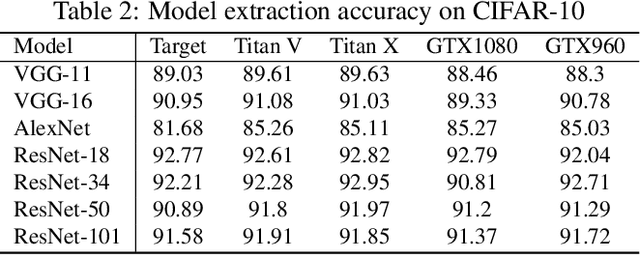
Neural network applications have become popular in both enterprise and personal settings. Network solutions are tuned meticulously for each task, and designs that can robustly resolve queries end up in high demand. As the commercial value of accurate and performant machine learning models increases, so too does the demand to protect neural architectures as confidential investments. We explore the vulnerability of neural networks deployed as black boxes across accelerated hardware through electromagnetic side channels. We examine the magnetic flux emanating from a graphics processing unit's power cable, as acquired by a cheap $3 induction sensor, and find that this signal betrays the detailed topology and hyperparameters of a black-box neural network model. The attack acquires the magnetic signal for one query with unknown input values, but known input dimensions. The network reconstruction is possible due to the modular layer sequence in which deep neural networks are evaluated. We find that each layer component's evaluation produces an identifiable magnetic signal signature, from which layer topology, width, function type, and sequence order can be inferred using a suitably trained classifier and a joint consistency optimization based on integer programming. We study the extent to which network specifications can be recovered, and consider metrics for comparing network similarity. We demonstrate the potential accuracy of this side channel attack in recovering the details for a broad range of network architectures, including random designs. We consider applications that may exploit this novel side channel exposure, such as adversarial transfer attacks. In response, we discuss countermeasures to protect against our method and other similar snooping techniques.

Model-Driven Feed-Forward Prediction for Manipulation of Deformable Objects

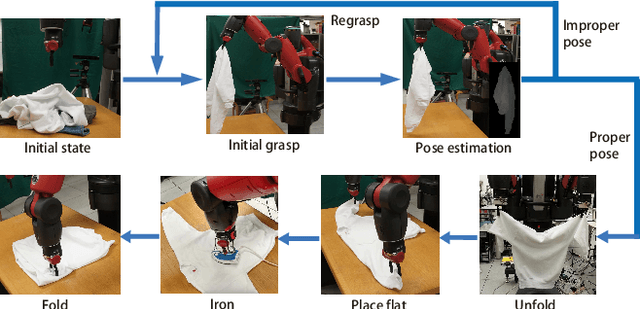
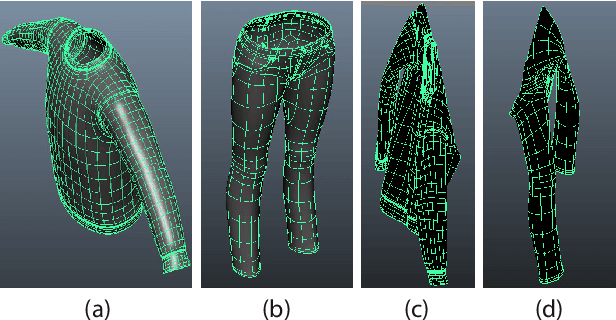
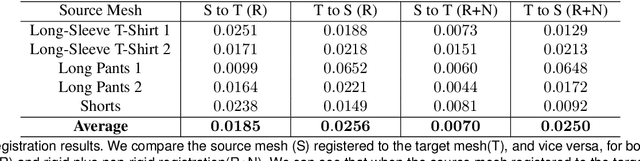
Robotic manipulation of deformable objects is a difficult problem especially because of the complexity of the many different ways an object can deform. Searching such a high dimensional state space makes it difficult to recognize, track, and manipulate deformable objects. In this paper, we introduce a predictive, model-driven approach to address this challenge, using a pre-computed, simulated database of deformable object models. Mesh models of common deformable garments are simulated with the garments picked up in multiple different poses under gravity, and stored in a database for fast and efficient retrieval. To validate this approach, we developed a comprehensive pipeline for manipulating clothing as in a typical laundry task. First, the database is used for category and pose estimation for a garment in an arbitrary position. A fully featured 3D model of the garment is constructed in real-time and volumetric features are then used to obtain the most similar model in the database to predict the object category and pose. Second, the database can significantly benefit the manipulation of deformable objects via non-rigid registration, providing accurate correspondences between the reconstructed object model and the database models. Third, the accurate model simulation can also be used to optimize the trajectories for manipulation of deformable objects, such as the folding of garments. Extensive experimental results are shown for the tasks above using a variety of different clothing.

Multi-Sensor Surface Analysis for Robotic Ironing

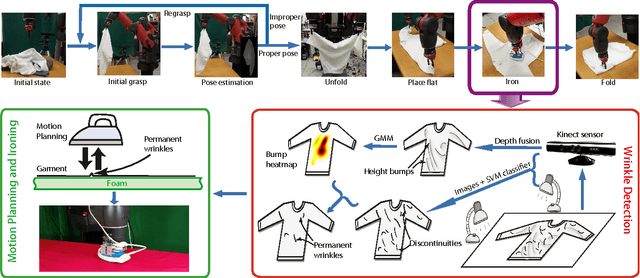
Robotic manipulation of deformable objects remains a challenging task. One such task is to iron a piece of cloth autonomously. Given a roughly flattened cloth, the goal is to have an ironing plan that can iteratively apply a regular iron to remove all the major wrinkles by a robot. We present a novel solution to analyze the cloth surface by fusing two surface scan techniques: a curvature scan and a discontinuity scan. The curvature scan can estimate the height deviation of the cloth surface, while the discontinuity scan can effectively detect sharp surface features, such as wrinkles. We use this information to detect the regions that need to be pulled and extended before ironing, and the other regions where we want to detect wrinkles and apply ironing to remove the wrinkles. We demonstrate that our hybrid scan technique is able to capture and classify wrinkles over the surface robustly. Given detected wrinkles, we enable a robot to iron them using shape features. Experimental results show that using our wrinkle analysis algorithm, our robot is able to iron the cloth surface and effectively remove the wrinkles.

Folding Deformable Objects using Predictive Simulation and Trajectory Optimization

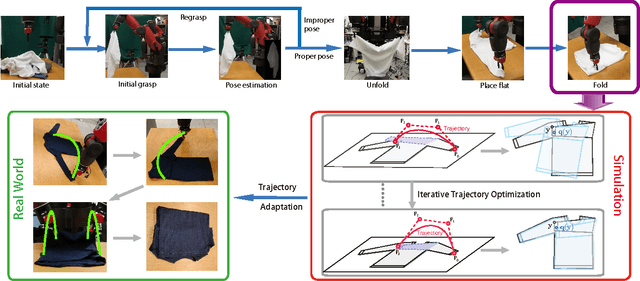
Robotic manipulation of deformable objects remains a challenging task. One such task is folding a garment autonomously. Given start and end folding positions, what is an optimal trajectory to move the robotic arm to fold a garment? Certain trajectories will cause the garment to move, creating wrinkles, and gaps, other trajectories will fail altogether. We present a novel solution to find an optimal trajectory that avoids such problematic scenarios. The trajectory is optimized by minimizing a quadratic objective function in an off-line simulator, which includes material properties of the garment and frictional force on the table. The function measures the dissimilarity between a user folded shape and the folded garment in simulation, which is then used as an error measurement to create an optimal trajectory. We demonstrate that our two-arm robot can follow the optimized trajectories, achieving accurate and efficient manipulations of deformable objects.