CROM: Continuous Reduced-Order Modeling of PDEs Using Implicit Neural Representations

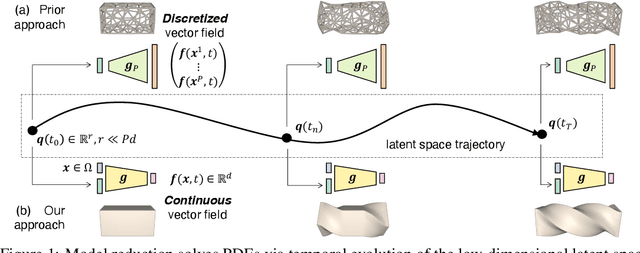
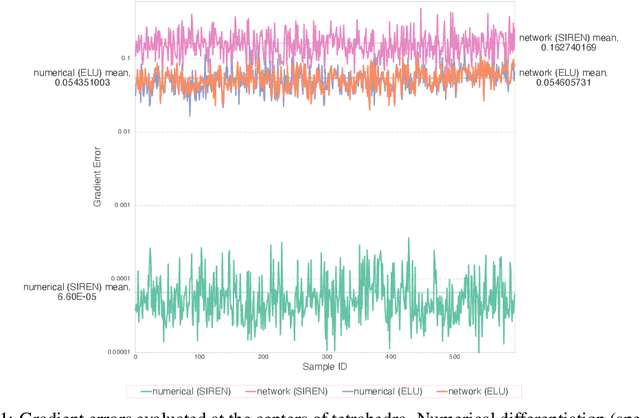
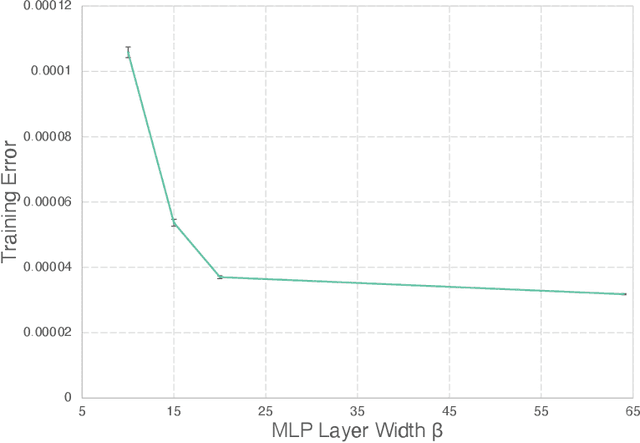
The excessive runtime of high-fidelity partial differential equation (PDE) solvers makes them unsuitable for time-critical applications. We propose to accelerate PDE solvers using reduced-order modeling (ROM). Whereas prior ROM approaches reduce the dimensionality of discretized vector fields, our continuous reduced-order modeling (CROM) approach builds a smooth, low-dimensional manifold of the continuous vector fields themselves, not their discretization. We represent this reduced manifold using neural fields, relying on their continuous and differentiable nature to efficiently solve the PDEs. CROM may train on any and all available numerical solutions of the continuous system, even when they are obtained using diverse methods or discretizations. After the low-dimensional manifolds are built, solving PDEs requires significantly less computational resources. Since CROM is discretization-agnostic, CROM-based PDE solvers may optimally adapt discretization resolution over time to economize computation. We validate our approach on an extensive range of PDEs with training data from voxel grids, meshes, and point clouds. Large-scale experiments demonstrate that our approach obtains speed, memory, and accuracy advantages over prior ROM approaches while gaining 109$\times$ wall-clock speedup over full-order models on CPUs and 89$\times$ speedup on GPUs.

Can one hear the shape of a neural network?: Snooping the GPU via Magnetic Side Channel

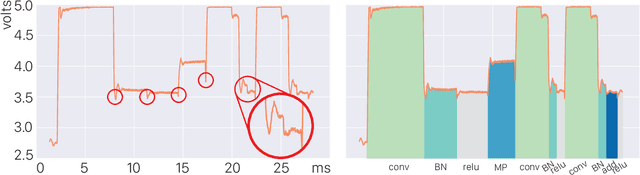
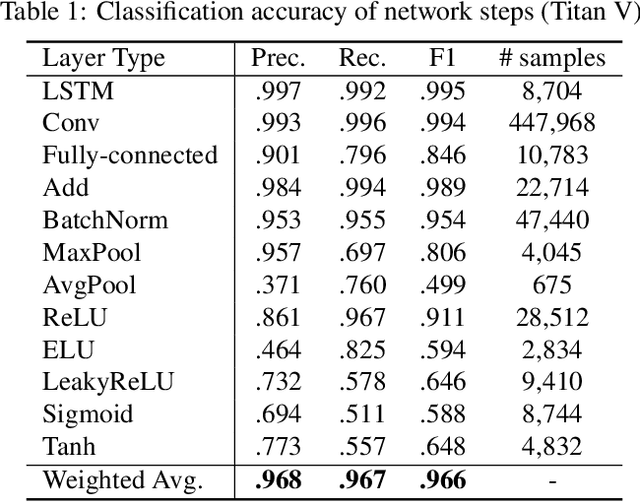
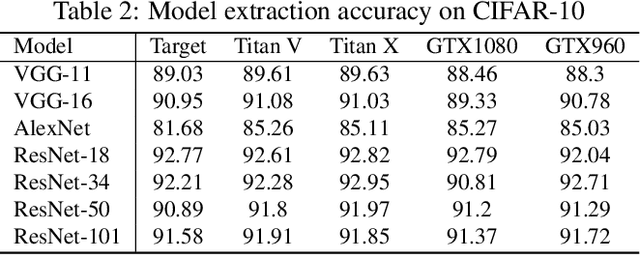
Neural network applications have become popular in both enterprise and personal settings. Network solutions are tuned meticulously for each task, and designs that can robustly resolve queries end up in high demand. As the commercial value of accurate and performant machine learning models increases, so too does the demand to protect neural architectures as confidential investments. We explore the vulnerability of neural networks deployed as black boxes across accelerated hardware through electromagnetic side channels. We examine the magnetic flux emanating from a graphics processing unit's power cable, as acquired by a cheap $3 induction sensor, and find that this signal betrays the detailed topology and hyperparameters of a black-box neural network model. The attack acquires the magnetic signal for one query with unknown input values, but known input dimensions. The network reconstruction is possible due to the modular layer sequence in which deep neural networks are evaluated. We find that each layer component's evaluation produces an identifiable magnetic signal signature, from which layer topology, width, function type, and sequence order can be inferred using a suitably trained classifier and a joint consistency optimization based on integer programming. We study the extent to which network specifications can be recovered, and consider metrics for comparing network similarity. We demonstrate the potential accuracy of this side channel attack in recovering the details for a broad range of network architectures, including random designs. We consider applications that may exploit this novel side channel exposure, such as adversarial transfer attacks. In response, we discuss countermeasures to protect against our method and other similar snooping techniques.