Thompson Sampling For Combinatorial Bandits: Polynomial Regret and Mismatched Sampling Paradox

We consider Thompson Sampling (TS) for linear combinatorial semi-bandits and subgaussian rewards. We propose the first known TS whose finite-time regret does not scale exponentially with the dimension of the problem. We further show the "mismatched sampling paradox": A learner who knows the rewards distributions and samples from the correct posterior distribution can perform exponentially worse than a learner who does not know the rewards and simply samples from a well-chosen Gaussian posterior. The code used to generate the experiments is available at https://github.com/RaymZhang/CTS-Mismatched-Paradox

ACPO: AI-Enabled Compiler-Driven Program Optimization

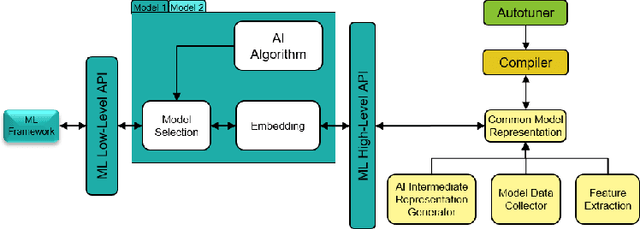
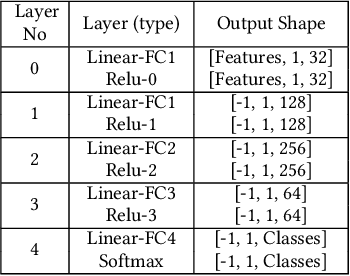
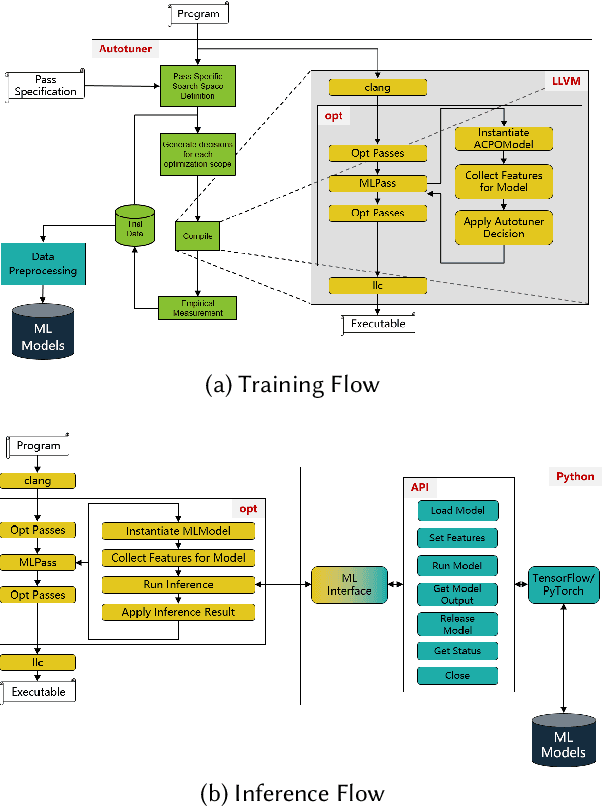
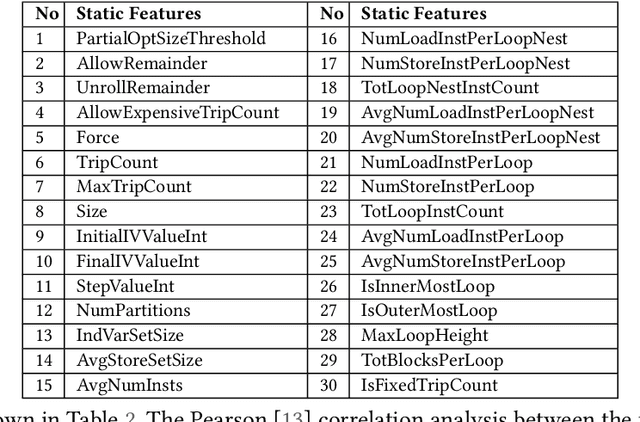
The key to performance optimization of a program is to decide correctly when a certain transformation should be applied by a compiler. Traditionally, such profitability decisions are made by hand-coded algorithms tuned for a very small number of benchmarks, usually requiring a great deal of effort to be retuned when the benchmark suite changes. This is an ideal opportunity to apply machine-learning models to speed up the tuning process; while this realization has been around since the late 90s, only recent advancements in ML enabled a practical application of ML to compilers as an end-to-end framework. Even so, seamless integration of ML into the compiler would require constant rebuilding of the compiler when models are updated. This paper presents ACPO: \textbf{\underline{A}}I-Enabled \textbf{\underline{C}}ompiler-driven \textbf{\underline{P}}rogram \textbf{\underline{O}}ptimization; a novel framework to provide LLVM with simple and comprehensive tools to benefit from employing ML models for different optimization passes. We first showcase the high-level view, class hierarchy, and functionalities of ACPO and subsequently, demonstrate \taco{a couple of use cases of ACPO by ML-enabling the Loop Unroll and Function Inlining passes and describe how ACPO can be leveraged to optimize other passes. Experimental results reveal that ACPO model for Loop Unroll is able to gain on average 4\% and 3\%, 5.4\%, 0.2\% compared to LLVM's O3 optimization when deployed on Polybench, Coral-2, CoreMark, and Graph-500, respectively. Furthermore, by adding the Inliner model as well, ACPO is able to provide up to 4.5\% and 2.4\% on Polybench and Cbench compared with LLVM's O3 optimization, respectively.

Reinforcement Learning for Traffic Signal Control: Comparison with Commercial Systems

Recently, Intelligent Transportation Systems are leveraging the power of increased sensory coverage and computing power to deliver data-intensive solutions achieving higher levels of performance than traditional systems. Within Traffic Signal Control (TSC), this has allowed the emergence of Machine Learning (ML) based systems. Among this group, Reinforcement Learning (RL) approaches have performed particularly well. Given the lack of industry standards in ML for TSC, literature exploring RL often lacks comparison against commercially available systems and straightforward formulations of how the agents operate. Here we attempt to bridge that gap. We propose three different architectures for TSC RL agents and compare them against the currently used commercial systems MOVA, SurTrac and Cyclic controllers and provide pseudo-code for them. The agents use variations of Deep Q-Learning and Actor Critic, using states and rewards based on queue lengths. Their performance is compared in across different map scenarios with variable demand, assessing them in terms of the global delay and average queue length. We find that the RL-based systems can significantly and consistently achieve lower delays when compared with existing commercial systems.

On the Suboptimality of Thompson Sampling in High Dimensions

In this paper we consider Thompson Sampling for combinatorial semi-bandits. We demonstrate that, perhaps surprisingly, Thompson Sampling is sub-optimal for this problem in the sense that its regret scales exponentially in the ambient dimension, and its minimax regret scales almost linearly. This phenomenon occurs under a wide variety of assumptions including both non-linear and linear reward functions. We also show that including a fixed amount of forced exploration to Thompson Sampling does not alleviate the problem. We complement our theoretical results with numerical results and show that in practice Thompson Sampling indeed can perform very poorly in high dimensions.