Efficient Function Placement in Virtual Networks: An Online Learning Approach

We propose a model for the virtual function placement problem and several novel algorithms using ideas based on multi-armed bandits. We prove that these algorithms learn the optimal placement policy rapidly, and their regret grows at a rate at most $O( N M \sqrt{T\ln T} )$ while respecting the feasibility constraints with high probability. We show through numerical experiments that those algorithms both have good practical performance and modest computational complexity. Using the proposed acceleration technique, they can be used to learn in large networks where computational power is limited. Our experiments are fully reproducible, and the code is publicly available.

Thompson Sampling For Combinatorial Bandits: Polynomial Regret and Mismatched Sampling Paradox

We consider Thompson Sampling (TS) for linear combinatorial semi-bandits and subgaussian rewards. We propose the first known TS whose finite-time regret does not scale exponentially with the dimension of the problem. We further show the "mismatched sampling paradox": A learner who knows the rewards distributions and samples from the correct posterior distribution can perform exponentially worse than a learner who does not know the rewards and simply samples from a well-chosen Gaussian posterior. The code used to generate the experiments is available at https://github.com/RaymZhang/CTS-Mismatched-Paradox

Towards Optimal Algorithms for Multi-Player Bandits without Collision Sensing Information

We propose a novel algorithm for multi-player multi-armed bandits without collision sensing information. Our algorithm circumvents two problems shared by all state-of-the-art algorithms: it does not need as an input a lower bound on the minimal expected reward of an arm, and its performance does not scale inversely proportionally to the minimal expected reward. We prove a theoretical regret upper bound to justify these claims. We complement our theoretical results with numerical experiments, showing that the proposed algorithm outperforms state-of-the-art in practice as well.

A High Performance, Low Complexity Algorithm for Multi-Player Bandits Without Collision Sensing Information

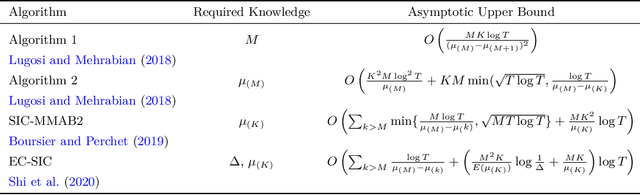
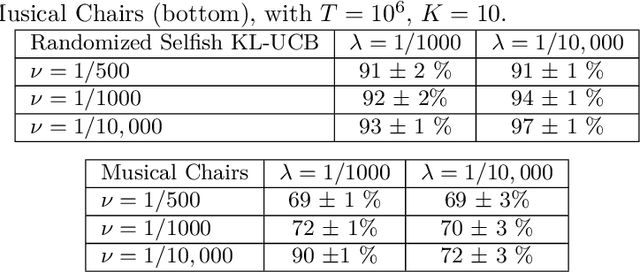
Motivated by applications in cognitive radio networks, we consider the decentralized multi-player multi-armed bandit problem, without collision nor sensing information. We propose Randomized Selfish KL-UCB, an algorithm with very low computational complexity, inspired by the Selfish KL-UCB algorithm, which has been abandoned as it provably performs sub-optimally in some cases. We subject Randomized Selfish KL-UCB to extensive numerical experiments showing that it far outperforms state-of-the-art algorithms in almost all environments, sometimes by several orders of magnitude, and without the additional knowledge required by state-of-the-art algorithms. We also emphasize the potential of this algorithm for the more realistic dynamic setting, and support our claims with further experiments. We believe that the low complexity and high performance of Randomized Selfish KL-UCB makes it the most suitable for implementation in practical systems amongst known algorithms.

Asymptotically Optimal Strategies For Combinatorial Semi-Bandits in Polynomial Time

We consider combinatorial semi-bandits with uncorrelated Gaussian rewards. In this article, we propose the first method, to the best of our knowledge, that enables to compute the solution of the Graves-Lai optimization problem in polynomial time for many combinatorial structures of interest. In turn, this immediately yields the first known approach to implement asymptotically optimal algorithms in polynomial time for combinatorial semi-bandits.

On the Suboptimality of Thompson Sampling in High Dimensions

In this paper we consider Thompson Sampling for combinatorial semi-bandits. We demonstrate that, perhaps surprisingly, Thompson Sampling is sub-optimal for this problem in the sense that its regret scales exponentially in the ambient dimension, and its minimax regret scales almost linearly. This phenomenon occurs under a wide variety of assumptions including both non-linear and linear reward functions. We also show that including a fixed amount of forced exploration to Thompson Sampling does not alleviate the problem. We complement our theoretical results with numerical results and show that in practice Thompson Sampling indeed can perform very poorly in high dimensions.

Solving Random Parity Games in Polynomial Time

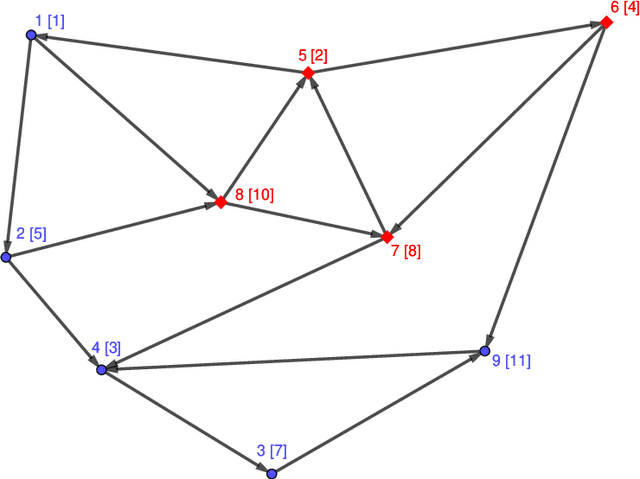
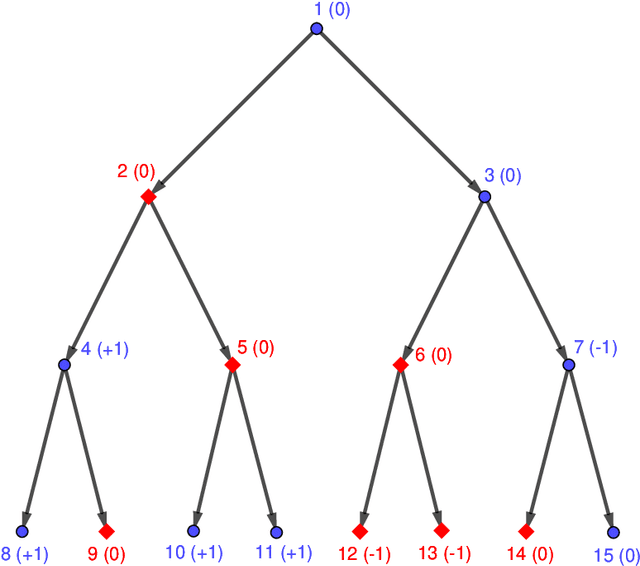
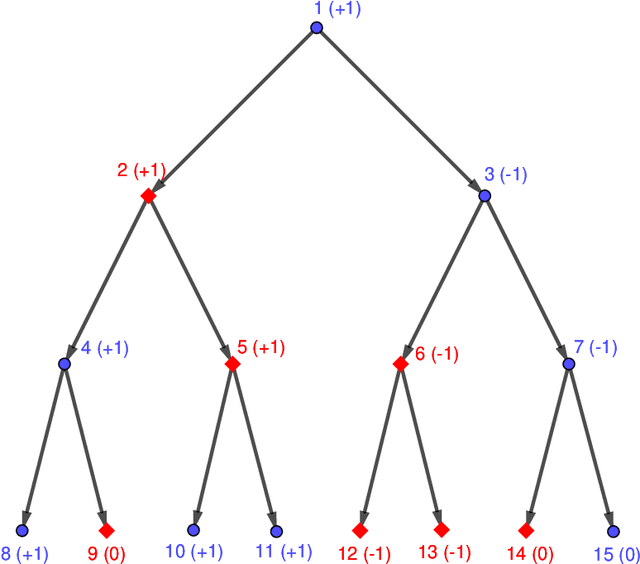
We consider the problem of solving random parity games. We prove that parity games exibit a phase transition threshold above $d_P$, so that when the degree of the graph that defines the game has a degree $d > d_P$ then there exists a polynomial time algorithm that solves the game with high probability when the number of nodes goes to infinity. We further propose the SWCP (Self-Winning Cycles Propagation) algorithm and show that, when the degree is large enough, SWCP solves the game with high probability. Furthermore, the complexity of SWCP is polynomial $O\Big(|{\cal V}|^2 + |{\cal V}||{\cal E}|\Big)$. The design of SWCP is based on the threshold for the appearance of particular types of cycles in the players' respective subgraphs. We further show that non-sparse games can be solved in time $O(|{\cal V}|)$ with high probability, and emit a conjecture concerning the hardness of the $d=2$ case.

Statistically Efficient, Polynomial Time Algorithms for Combinatorial Semi Bandits

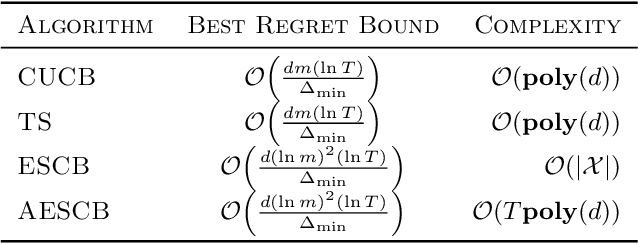
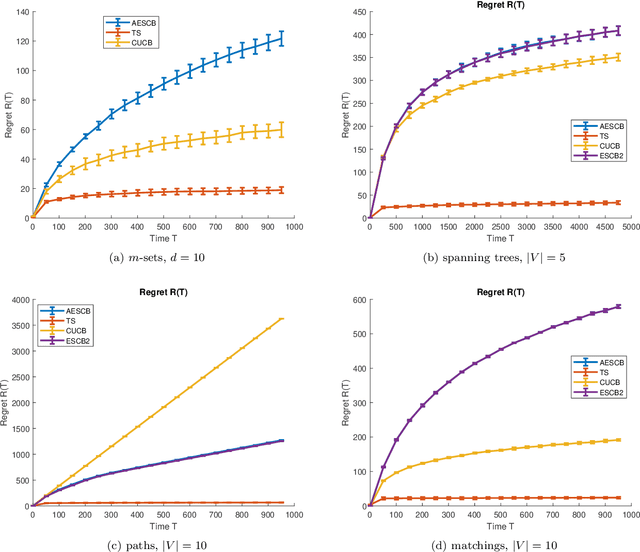
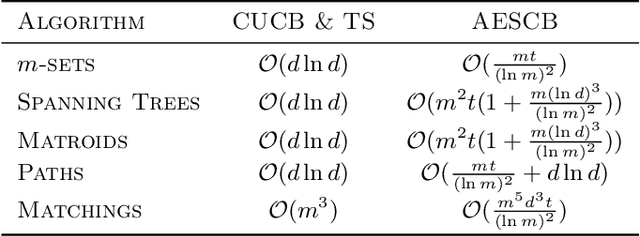
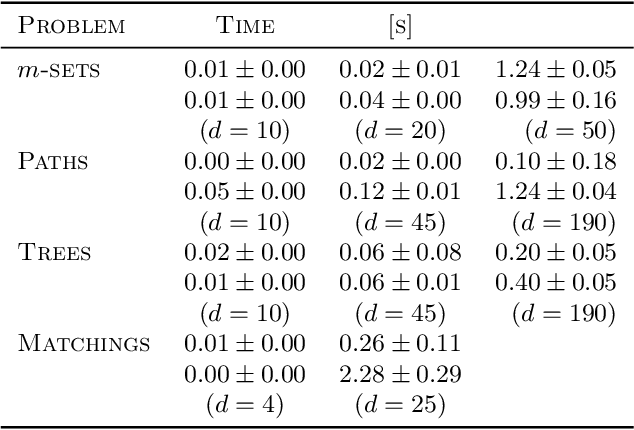
We consider combinatorial semi-bandits over a set of arms ${\cal X} \subset \{0,1\}^d$ where rewards are uncorrelated across items. For this problem, the algorithm ESCB yields the smallest known regret bound $R(T) = {\cal O}\Big( {d (\ln m)^2 (\ln T) \over \Delta_{\min} }\Big)$, but it has computational complexity ${\cal O}(|{\cal X}|)$ which is typically exponential in $d$, and cannot be used in large dimensions. We propose the first algorithm which is both computationally and statistically efficient for this problem with regret $R(T) = {\cal O} \Big({d (\ln m)^2 (\ln T)\over \Delta_{\min} }\Big)$ and computational complexity ${\cal O}(T {\bf poly}(d))$. Our approach involves carefully designing an approximate version of ESCB with the same regret guarantees, showing that this approximate algorithm can be implemented in time ${\cal O}(T {\bf poly}(d))$ by repeatedly maximizing a linear function over ${\cal X}$ subject to a linear budget constraint, and showing how to solve this maximization problems efficiently.

Solving Bernoulli Rank-One Bandits with Unimodal Thompson Sampling

Stochastic Rank-One Bandits (Katarya et al, (2017a,b)) are a simple framework for regret minimization problems over rank-one matrices of arms. The initially proposed algorithms are proved to have logarithmic regret, but do not match the existing lower bound for this problem. We close this gap by first proving that rank-one bandits are a particular instance of unimodal bandits, and then providing a new analysis of Unimodal Thompson Sampling (UTS), initially proposed by Paladino et al (2017). We prove an asymptotically optimal regret bound on the frequentist regret of UTS and we support our claims with simulations showing the significant improvement of our method compared to the state-of-the-art.

Computationally Efficient Estimation of the Spectral Gap of a Markov Chain

We consider the problem of estimating from sample paths the absolute spectral gap $\gamma_*$ of a reversible, irreducible and aperiodic Markov chain $(X_t)_{t \in \mathbb{N}}$ over a finite state $\Omega$. We propose the ${\tt UCPI}$ (Upper Confidence Power Iteration) algorithm for this problem, a low-complexity algorithm which estimates the spectral gap in time ${\cal O}(n)$ and memory space ${\cal O}((\ln n)^2)$ given $n$ samples. This is in stark contrast with most known methods which require at least memory space ${\cal O}(|\Omega|)$, so that they cannot be applied to large state spaces. Furthermore, ${\tt UCPI}$ is amenable to parallel implementation.