Solving Random Parity Games in Polynomial Time

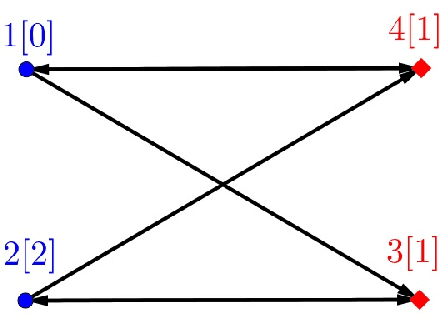
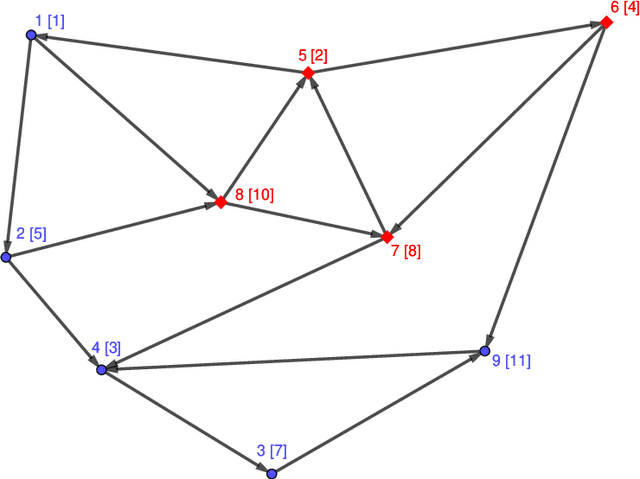
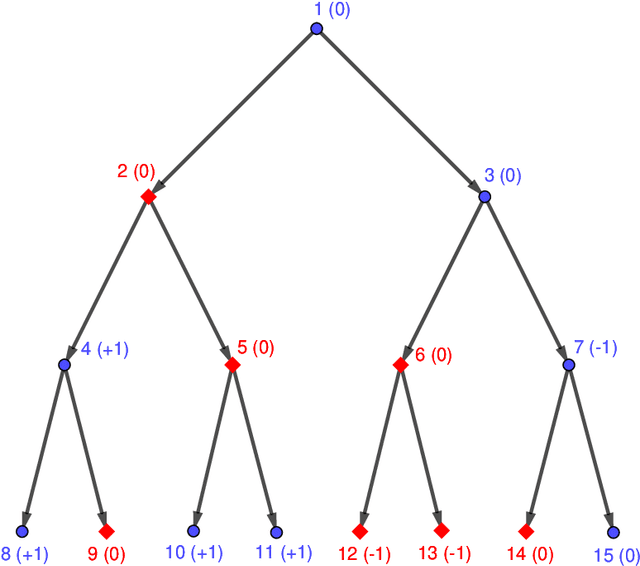
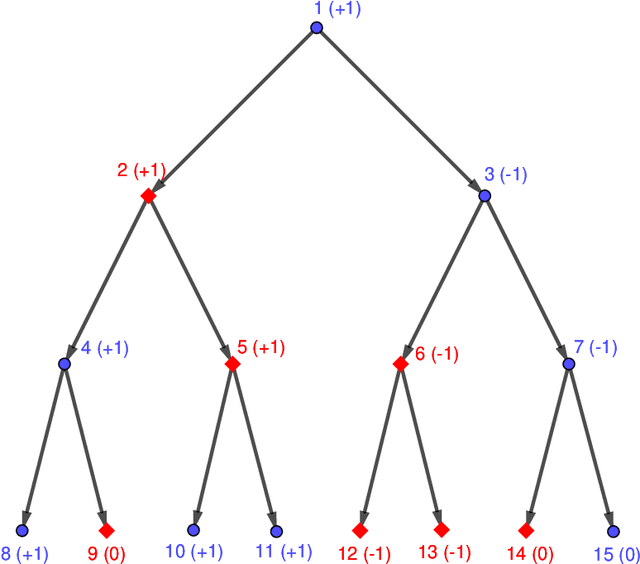
We consider the problem of solving random parity games. We prove that parity games exibit a phase transition threshold above $d_P$, so that when the degree of the graph that defines the game has a degree $d > d_P$ then there exists a polynomial time algorithm that solves the game with high probability when the number of nodes goes to infinity. We further propose the SWCP (Self-Winning Cycles Propagation) algorithm and show that, when the degree is large enough, SWCP solves the game with high probability. Furthermore, the complexity of SWCP is polynomial $O\Big(|{\cal V}|^2 + |{\cal V}||{\cal E}|\Big)$. The design of SWCP is based on the threshold for the appearance of particular types of cycles in the players' respective subgraphs. We further show that non-sparse games can be solved in time $O(|{\cal V}|)$ with high probability, and emit a conjecture concerning the hardness of the $d=2$ case.

Computationally Efficient Estimation of the Spectral Gap of a Markov Chain

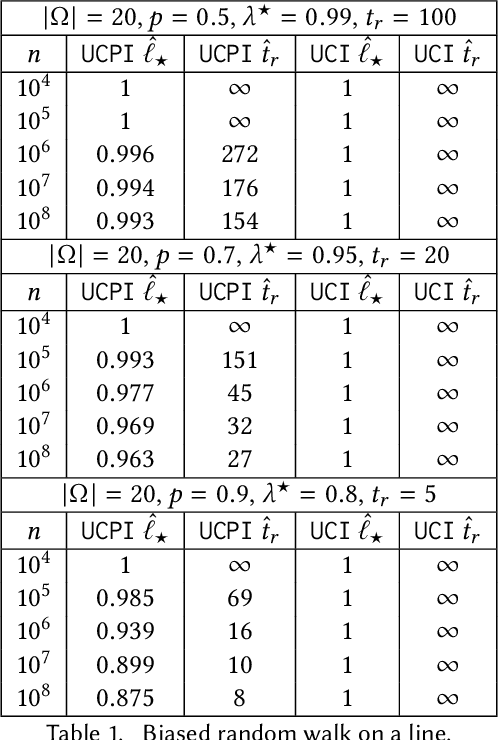
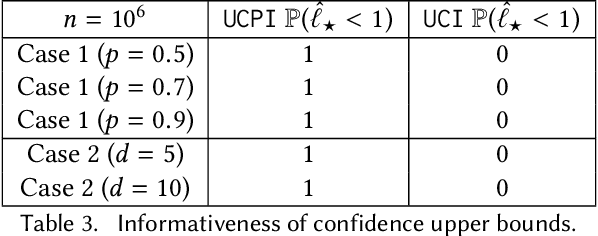
We consider the problem of estimating from sample paths the absolute spectral gap $\gamma_*$ of a reversible, irreducible and aperiodic Markov chain $(X_t)_{t \in \mathbb{N}}$ over a finite state $\Omega$. We propose the ${\tt UCPI}$ (Upper Confidence Power Iteration) algorithm for this problem, a low-complexity algorithm which estimates the spectral gap in time ${\cal O}(n)$ and memory space ${\cal O}((\ln n)^2)$ given $n$ samples. This is in stark contrast with most known methods which require at least memory space ${\cal O}(|\Omega|)$, so that they cannot be applied to large state spaces. Furthermore, ${\tt UCPI}$ is amenable to parallel implementation.